话说这场比赛的题名字好像都是 Taylor Swift 的歌名。
题意
有一个由罐子排列成的金字塔,罐子自上而下依次编号:
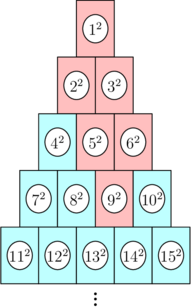
现在你要打下一个罐子,则与其有关的所有罐子也会被击落,计算所有被击落的罐子编号的平方和。
比如说,你击中了 \(9\) 号罐子,则上图中所有标红的罐子都会被击落。
\(n \le 10^6\)。多测,\(t \le 10^3\)。
思路
乍一看好像很不好找出与一个罐子有关的所有罐子的编号?但是,我们可以把原图旋转一下,得到一个矩阵:
\[\begin{pmatrix} \color{red}{1} & \color{red}{3} & \color{red}{6} & 10 & 15 & \cdots \\ \color{red}{2} & \color{red}{5} & \color{red}{9} & 14 & 20 & \cdots \\ 4 & 8 & 13 & 19 & 26 & \cdots \\ 7 & 12 & 18 & 25 & 33 & \cdots \\ 11 & 17 & 24 & 32 & 41 & \cdots \\ \vdots & \vdots & \vdots & \vdots & \vdots & \ddots \end{pmatrix} \]这看上去是个无穷矩阵,但事实上由于题目中给出的 \(n \le 10^6\),因此矩阵中的元素个数是有限的。
观察这个矩阵,我们得到:与某个数字相关的所有数字共同构成这个数字所在位置的左上方的矩形。比如说,与 \(9\) 有关的数字(上图中标红的数字)刚好都在 \(9\) 左上方的矩形中。
于是现在的问题就转化为了一个二维前缀和,即:求出 \(n\) 左上角这个矩形中所有数字的平方和。如果我们能构造出这个矩阵的话,这当然是很容易的。
如何构造这个矩阵呢?观察得到矩阵中每一行与每一列的数字间都存在很强的递变规律,记上述的矩阵为 \(A\),则有 \(A_{i, j} = A_{i, j - 1} + i + j - 1 = A_{i - 1, j} + i + j - 2\)。于是我们就可以通过这个关系求出具体的矩阵 \(A\),记录下每个数字的坐标,在其上做二维前缀和就可以求出答案。
还有一种思路,即我的实现方法,就是找出每一行每一列增量的变化关系,这个其实与上边的做法本质相同,就不多说了。
我的具体实现稍有不同,我是先计算出每一行的前缀平方和,再将其与前边的行的前缀平方和累加来计算出每个数字对应的答案的。
由于这个矩阵不会随 \(n\) 变化,因此我们可以把它预处理出来,这样就可以做到单次询问 \(O(1)\),于是总的时间复杂度为 \(O(\max(n) + t)\)。
代码
代码中的 pre[i] 即为数字 \(i\) 所在行的前缀和,f[i] 即为 \(i\) 对应的答案。
#include <bits/stdc++.h>
using i64 = long long;
static std::vector<i64> f(1e6 + 1);
void init() {
f[1] = 1;
std::vector a(1.5e3, std::vector<i64>(1.5e3));
std::vector<i64> pre(1e6 + 1);
int d1 = 1, row = 0;
for (int i = 1; i <= 1e6; i += d1, d1++, row++) {
int d2 = 1 + d1, col = 0;
for (int j = i; j <= 1e6; j += d2, d2++, col++) {
a[row][col] = j;
pre[j] = (i64) j * j + (col ? pre[a[row][col - 1]] : 0);
f[j] = pre[j] + (row ? f[a[row - 1][col]] : 0);
}
}
return;
}
void solve() {
int n;
std::cin >> n;
std::cout << f[n] << "\n";
return;
}
int main() {
std::ios::sync_with_stdio(false);
std::cin.tie(0);
init();
int t;
std::cin >> t;
while (t--) {
solve();
}
return 0;
}