题目描述
pipi 和 lili 各带来一个正多边形卡片。
pipi 的卡片是边长为 \(A\) 的正 \(M\) 边形,lili 的卡片是边长为 \(B\) 的正 \(N\) 边形。
pipi 和 lili 将两张卡片摆放在一起,其中两张卡片并不重叠,并且有至少一个公共顶点和一条公共边。
pipi 喜欢旋转,因此她沿 lili 的卡片顺时针旋转自己的多边形。旋转的中心点是多边形公共边上一点,且旋转过程中两张卡片不重叠。
pipi 想知道,在旋转多少次过后,pipi 的正多边形会回到原位置。
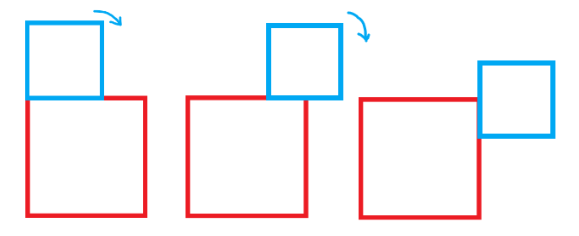
【例如】:pipi 的卡片是边长为 \(2\) 的正 \(4\) 边形,lili 的卡片是边长为 \(3\) 的正 \(4\) 边形。
前两次旋转如图所示:
输入格式
一行,四个整数 \(A,M,B,N\) ,含义如题目描述所述。
输出格式
一行,一个数 \(Ans\) ,表示 pipi 旋转的次数。
样例输入
2 4 3 4
样例输出
8
提示
对于 \(100\%\) 的数据,\(1 ≤ A ≤ B ≤ 10^6\) ,\(3 ≤ N,M ≤ 10^6\) 。
很有意思的一道题目
不难看出,如果 \(A\) 从 \(B\) 的一条边旋转到另一条边,两次接触 \(B\) 的长度之和必定是 \(A\) 的边长
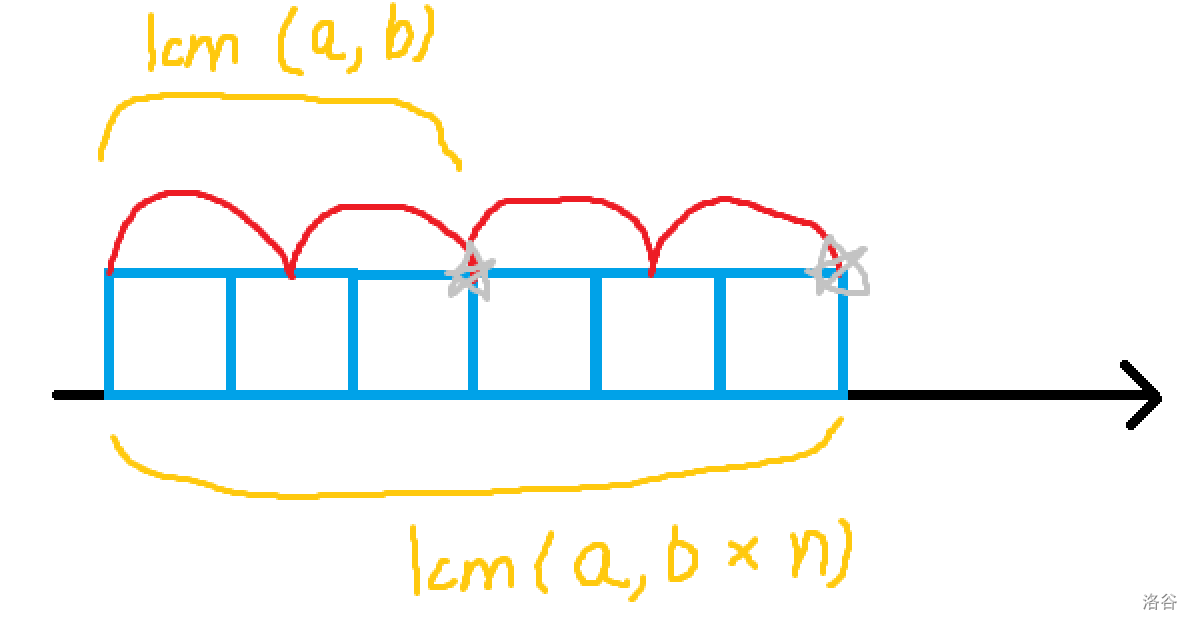
那么便可以把 \(A\) 每次旋转出来的图形表示在一根数轴上
也就是说 \(A\) 的个数就是 \(A\) 的边长与 \(B\) 的周长的最小公倍数,再除以 \(A\) 的边长
但我们忽略了一点,当我们把这些旋转出来的图形放在数轴上时,有一部分没有放上去,那便是转角处的 \(A\)
转角处的 \(A\) 有两种情况,一种是刚好有一个顶点与 \(B\) 重合,这在第一次已经算过了,要删掉,第二种便是普通情况
普通情况下就是 \(A\) 的边长与 \(B\) 的周长的最小公倍数,再除以 \(B\) 的边长即可
特殊情况则需要 \(A\) 的边长与 \(B\) 的边长的最小公倍数,这个便是每隔多长会出现一次特殊情况
再用 \(A\) 的边长与 \(B\) 的周长的最小公倍数除以这个数便是特殊情况的个数
顺便放张样例转化成这个思路的图,自行体会吧
\(Code:\)
#include<bits/stdc++.h>
#define int long long//不开long long见祖宗
using namespace std;
int a,m,b,n;
int gcd(int a,int b){
if(a%b==0) return b;
else return gcd(b,a%b);
}
int lcm(int a,int b){
return a*b/gcd(a,b);
}
signed main()
{
scanf("%lld%lld%lld%lld",&a,&m,&b,&n);
int x=lcm(a,n*b);
int c1=x/a;
int y=lcm(a,b);
int c2=x/b-x/y;
printf("%lld",c1+c2);
return 0;
}