ARC

ARC121D 1 or 2

先考虑没有选一个的情况

这个玩意感觉就很最小和最大加，次小和次大加……仔细想想发现是对的

然后发现选一个和选一个和 \(0\) 一样，所以就枚举有几个是选一个的，往序列里面补上 \(0\) 就好了

code

ARC121E Directed Tree

容斥

让求恰好 \(0\) 个 \(a_i\) 是 \(i\) 父亲，发现直接做根本没思路，又发现我们会求至少 \(x\) 个 \(a_i\) 是 \(i\) 父亲，这个直接背包就好了，枚举当前节点可以做哪个节点的 \(a_i\) ，然后直接容斥就好了

ARC122D XOR Game

洛谷题意是错的

正确题意：黑板上有 \(2n\) 个数，现在有两个人分别选数，先手选一个数 \(x\)，后手选一个数 \(y\)，将 \(x\ xor \ y\) 写在纸上，将 \(x,y\) 从黑板上擦出，先手希望纸上的数的 \(\max\) 最大，后手希望纸上的 \(\max\) 最小，求博弈后结果

看道异或肯定是按位考虑

从高位向低位做

如果当前 \(solve\) 区间的当前位有偶数个 \(0\) ，那就按当前位分开继续递归

若果当前 \(solve\) 区间的当前位有奇数个 \(0\) ，发现我不管怎么配对当前位都会有一个是 \(1\) ，考虑让这个数最小，这个 \(01trie\) 可以搞

最后把所有区间答案取 \(\max\) 就行了

没看懂就看代码吧 code

ARC122E Increasing LCMs

考虑什么时候可以填一个数，当填到 \(i-1\) 时，满足 \(\sum\limits_{i=1}^{i-1}\gcd\{\frac{A_x}{\gcd(A_x,x_i)}\} \ne 1\) 时可以填进去，发现我正着填会依据我之前填了什么来判断现在的能不能填，这样是不好做的，但是要是反过来填，确定最后一个填什么后我就知道 \(x\) 数组了，这样就很容易确定最后一个填什么，如果有多个的话显然填哪个都行，递归下去全部填上就好了

code

ARC122F Domination

先套路的把包含的红点点全部删掉，剩下的点是横坐标递增，纵坐标递减的

先考虑 \(k=1\) 怎么做：

发现还是不会，那么再加上限制条件：只有一个蓝点

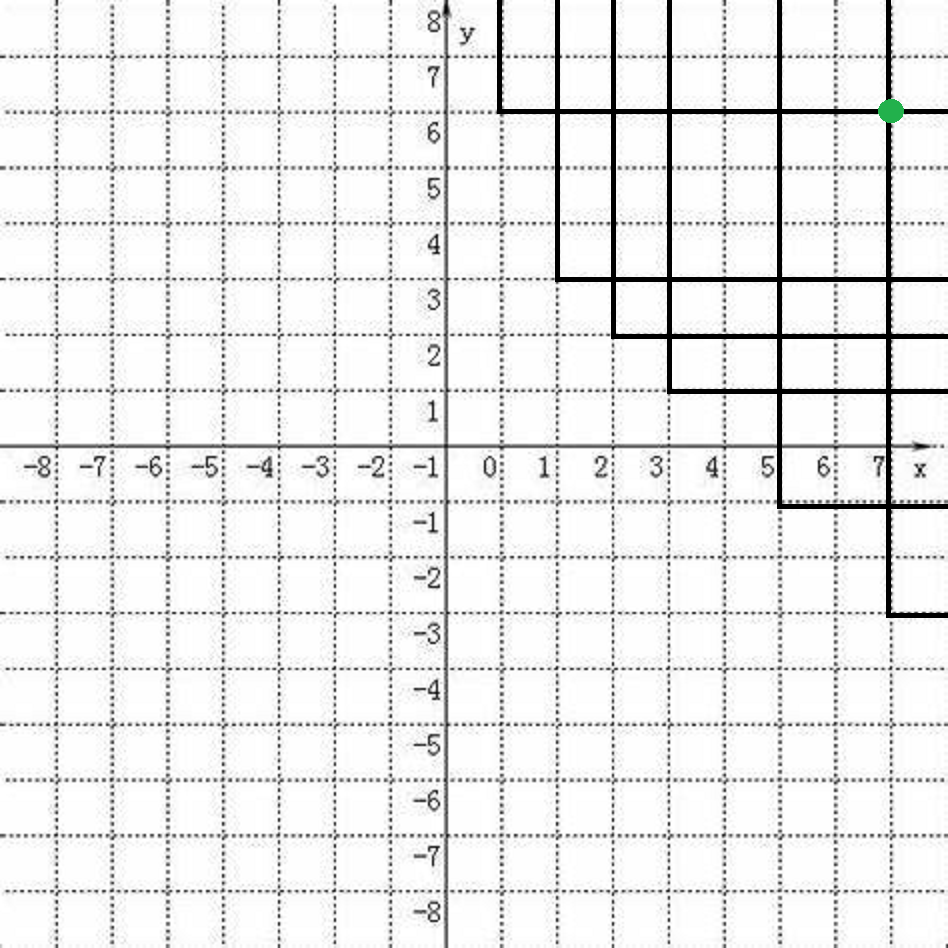
发现其实就是把蓝点移动到 \((x_n,y_1)\)，即横坐标最大，纵坐标最小的点的右上角，就是上图的绿点右上角，黑框的左下角是红点

那么怎么扩展到有很多蓝点呢？

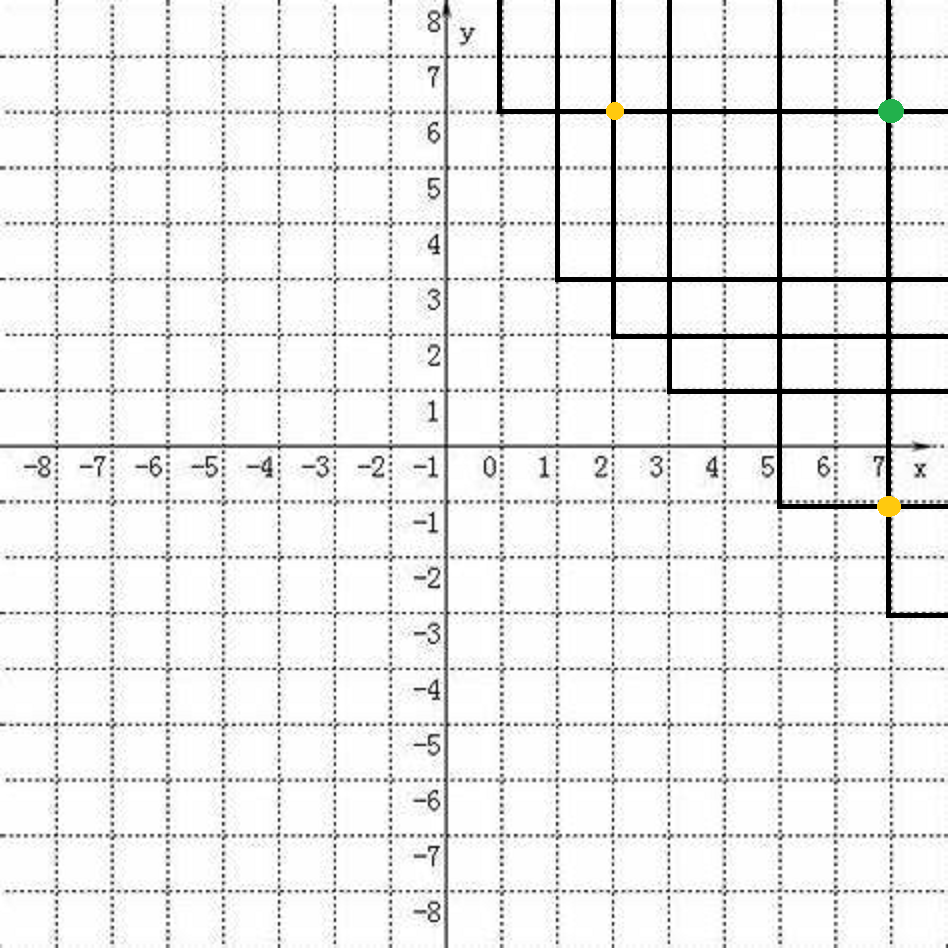
我们发现让一个蓝点覆盖一个不连续的区间是一定不优的，比如这样，发现不管哪里走到两个黄点都不如直接走到绿点，所以可以去掉蓝点一个一次的性质，这样直接 \(dp\) 是 \(O(n^3)\) 写个 \(kdt\) 估计能优化一点，但是跟正解没啥关系。

\(dp\) 应该是没啥出路了，考虑一个可以刻画这个 \(dp\) 的东西，因为是曼哈顿距离，考虑将二维坐标拆成两个以为坐标，横坐标从大往小连，纵坐标从小往大连，这么连可以理解为横坐标是红点在向外移动，因为我要从红点开始走，纵坐标是蓝点在移动，正边权值是坐标距离之差，反边权值为 \(0\) ，然后对于所有的蓝点 \((x_i,y_i)\) ，连一条横坐标数轴上点 \(x_i\) 到纵坐标数轴上点 \(y_i\) 的边，权值为 \(0\) ，发现现在将红点点集合 \([i,j]\) 覆盖的改价是 \(|x_j-x_k|+|y_i-x_k|,k\) 是我用的蓝点编号，这玩意就是 \(x_j\) 到 \(y_i\) 的最短路，然后再加上 \(y_i\) 到 \(x_{i-1}\) 的边就可以处理有很多蓝点的情况了，这样连是因为发现我初始是从最后一个点走的，所以是 \(i\) 向 \(i-1\)

考虑 \(k \ne 1\) 怎么做，其实跟上面一样，跑一个费用流就好了，跑 \(Primal-Dual\) 的时间复杂度是 \(O(km\log m),m\) 是边数

code

ARC123D Inc, Dec - Decomposition

构造题

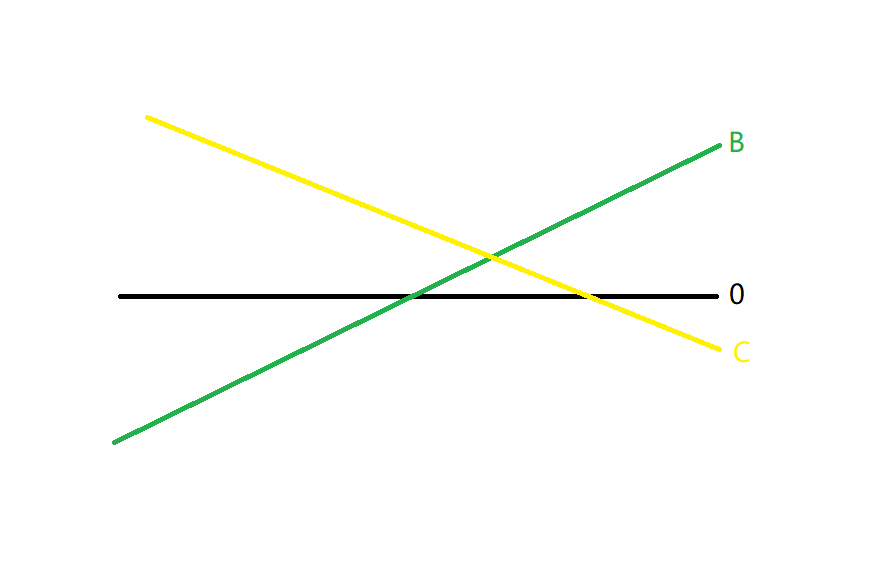
假设现在求出来了一种 \(B,C\) 序列，但是这样不一定是最优的，我可以整体向上平移 \(B\) 然后再向下平移 \(C\) ,这样还是一组解

至于什么时候平移到的是最优的呢

一个向上一个向下不太好做，所以考虑将\(C\) 序列对折过来，然后平移到与 \(B\) 重合，现在平移就是一起向上/向下平移了，最优解现在就把题目转化成了货仓选址

然后考虑怎么构造

初始将 \(B_1\) 设为 \(0\) ，将 \(C_1\) 设为 \(A_1\)，然后考虑 \(A_i\) 与 \(A_{i+1}\) 之间的大小关系

当 \(A_i \ge A_{i+1}\) 时，我们让 \(B_{i+1}=B_{i}-(A_{i+1}-A_i)\) ，\(C_{i+1}=C_i\)

当 \(A_i < A_{i+1}\) 时，我们让 \(B_{i+1}=B_{i}\) ，\(C_{i+1}=C_i+(A_{i+1}-A_i)\)

然后根据上面的平移

证明：

首先这肯定是符合题目条件的

然后分类讨论：

当 \(B\) 没有负数时，\(B+C=A\) 这肯定是最小的

当 \(B\) 有负数时，发现我刚才的构造方法都是让 \(C\) 最大的，也就是 \(B\) 最小，这样肯定是优的

ARC124D Yet Another Sorting Problem

不难的题

首先套路的搞出置换环，手玩一下发现要是环上颜色不是全部相同就可以用 \(环长-1\) 消去，考虑一个纯色环怎么办，发现颜色不同的纯色环可以两两合并，费用为 \(1\) ，要是只有一种纯色环那就随便找一个环合并，费用为 \(2\) ，不难发现这样是最优的。

ARC126D Pure Straight

题意：给定一个长度为 \(n \le 200\) 的序列，\(a_i \in [1,k],k<=16\) ，每次操作可以交换相邻的两项，求最少多少次操作可以使序列 \(A\) 有一个子串满足 \(A_x=1,A_{x+1}=2…A_{x+k-1}=k\)

\(k \le 16\) ，考虑状压，设 \(f_{i,s}\) 表示现在考虑到了序列第 \(i\) 位，现在排好的序列出现的数的集合是 \(s\) 的最小步数，考虑 \(i\) 选不选，选的代价是 \(popcount(s>>(a_i-1))\) ，如果不选现在的序列要往前移动一步，或者我以后会放到序列里面的往后移动一步，代价是 \(\min(popcount(s),m-popcount(s))\) ，然后就 \(dp\) 就好了

code

ARC126E Infinite Operations

第一眼感觉不会做，但是总价值肯定是一个根 \(\sum\limits_{j=1}^{n}\sum\limits_{i=1}^{j-1}|a_i-a_j|\) 之类相关的东西，设 \(F(a)=\sum\limits_{j=1}^{n}\sum\limits_{i=1}^{j-1}|a_i-a_j|\) ，手玩一下发现好像是对相邻两项操作是最优的，发现要是对相邻两项操作 \(x\) 的话 \(F(a)\) 会减少 \(2x\) ，最后 \(F(a)\) 会变成 \(0\) ，但是要是你操作的不是相邻两项，发现他的代价一定是大于等于 \(2x\) ，发现我这样操作一定不劣，所以答案就是 \(\frac{F(a)}{2}\) ，我修改一个点就是要求前后缀和，用线段树搞一下就好了

[code](Submission #40930728 - AtCoder Regular Contest 126)

ARC127D Sum of Min of Xor

看见异或考虑 \(01trie\) ，但是因为有两个数组，一般的 \(01trie\) 好像搞不了，考虑搞一个四叉 \(01trie\) 分别表示 \(A,B : 0/0,0/1,1/0,1/1\) ，对于每一个数对统计答案的时候递归，如果往一个儿子走两个数异或值不一样了发现可以记一个子树每一位个数和的东西直接统计，但是要是异或值相同的话你会递归两个儿子，复杂度就不对了，但是观察发现异或若 \(0/1\) 相同，那么 \(1,0\) 一定相同，\(0/0,1/1\) 同理，所以可以合并 \(0/1,1/0\) 和 \(0/0,1/1\) ，这样就只有两个儿子了，可以直接做了

code （ \(sum_{a,b,c,u,x}\) 的意思现在在节点 \(u\) ，当前统计的是第 \(a:0/1\) 个数组的 \(sum\) ，现在的情况 (\(0/0,0/1,1/0,1/1\)) 是 \(b\) ，第 \(x\) 位的值是 \(c\) 个数

ARC127E Priority Queue

想反了浪费一上午

很容易发现 \(s\) 里面的元素单调递增是最优的，这样我们要是填到 \(i-1\) 要填 \(i\) 的时候就知道 \(i\) 要填的数的下界了，显然要是第 \(i\) 位 \(x\) 能填那么小于 \(x\) 的一定也是能填的，所以我们要是知道上界就非常好做了，那么上界是什么呢，发现按照题意模拟，第 \(i\) 要是要填数就填 \(i\) 就行了，不难发现这样是最优的，因为你删掉的都是能删掉的最小的，所以就可以直接 \(dp\) 了

code

ARC129D -1+2-1

首先 \(\sum\limits_{i=1}^{n}a_i \ne 0\) 肯定寄

设位置 \(i\) 选了 \(x_i\) 次，那么现在的要求就是 \(a_i+2x_i-x_{i-1}-x_{i+1}=0\) ，发现这个玩意很像 \(x\) 的差分数组，设 \(d_i=x_i-x_{i-1}\) ，这样要求就是 \(d_{i+1}-d_i=a_i\) 了（这里下标都是 \(\bmod n\) 意义下的

把 \(d_i-d_{i-1}\) 前缀和一下，得到 \(d_i-d_1=\sum\limits_{j=1}^{i-1}a_j\) ，即 \(d_i=\sum\limits_{j=1}^{i-1}a_j+d_1\) ，发现只要知道 \(d_1\) 我就可以知道所有东西了，考虑怎么算 \(d_1\)

我们知道 \(\sum\limits_{i=1}^{n}d_i=\sum\limits_{i=1}^{n} (x_i-x_{i-1})=0\) ，所以 \(\sum\limits_{i=1}^{n}d_i=\sum\limits_{i=1}^{n}\sum\limits_{j=1}^{i-1}a_j+n \times d_1=n\times d_1+\sum\limits_{i=1}^{n}(n-i)a_i=0\)

所以 \(d_1=-\frac{\sum\limits_{i=1}^{n}(n-i)a_i}{n}\)

如果 \(d_1\) 不是整数那么就是无解

现在考虑怎么算 \(x\)

显然 \(x_i=\sum\limits_{j=2}^{i} d_j+x_1\) ，所以我们其实是要让 \(x_1\) 最小

因为 \(x_i \ge 0\) 所以 \(x_1\) 很好求出来

code

ARC130D Zigzag Tree

发现我的根在哪里很重要，设 \(f_{u,x,0/1}\) 表示我现在\(dp\) 到节点 \(u\) ，根节点填的数排名为 \(x\) ，我要周围节点都比我大(小)的方案数

考虑怎么合并两个序列，枚举我当前根节点前面有几个子节点的序列里面的，发现第三维要是 \(0\) 就一定要有子节点，否则一定没有，也就是做一个前缀和就好了

code

ARC146D >=<

不难

最小的肯定是全部填 \(1\) ，但是现在还有限制，因为我现在是要最小的，所以能等于一定等于，大于一定是等于 \(+1\) ，所以连边 \(p_i,x_i,q_i,y_i\) ，表示要是我点 \(p_i\) 要是大于 \(x_i\) 的话那就更新 \(q_i\) 为 \(y_i\) ，还有就是大于的情况，连边 \(p_i,x_i+1,q_i,y_i+1\) ，意义和上面一样，不难发现这样是对的

code