P7603 [THUPC2021] 鬼街(减半警报器模板)
前言
这是一个由 lxl 大佬提出的神奇 trick,第一次省选集训的时候有点颓,听完了没写。刚好明天又要讲这个不如写篇题解。
还是,我太弱了;所以又是研究一晚上才写出来,所以还是吧我对这道题的理解讲讲。
正文
何为折半报警器
按照 lxl 的 ppt 上的话来说是这样的:
这种题目一般是你需要维护一个数据结构,初始给定了一些范围,每个范围有权值。每次把包含一个点的所有范围都减去 $x$。你需要维护每个范围被减到 $<0$ 的最早时刻。
图一:
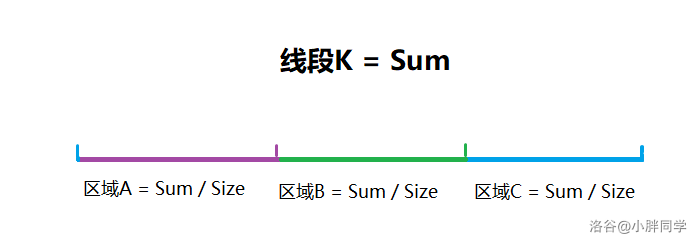
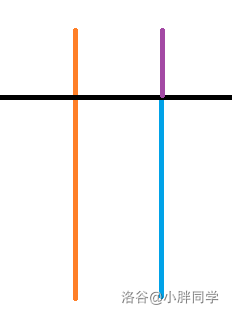
图二:

具象一点说,当每个检测的区间是由多个独立子区间构成,多个区间可能用到相同的子区间,我们就有可能用到他。
多个独立子区间构成就如图一,我们可以不重不漏的吧一个区间分成多个子区间。
个区间可能用到相同的子区间,也就是说我们存子区间的时候可以讲重复子区间可以同时存在一起,如果按照图像来说就可以相当于(图二)把子区间平移。
由于线段的值是子区间的和,呢么一定有至少一个子区间是大于 $\frac{Sum}{Size}$ 的,如果有一个子区间被将为 $0$ 一下,我们就将线段重新平分。
整体而言并不是讲所有区间实时更新,而是在子区间被将为 $0$ 时再对改线段重新同步。
本题如何实现
读完题目会发现,这道题就符合了所说的“当每个检测的区间是由多个独立子区间构成,多个区间可能用到相同的子区间”。我们可以吧每个质因子作为一个子区间维护。
具体而言,我们首先为了将数质因数分解,需要先筛出素数。
后对于增加报警器的操作,因为报警器只能检测安放后的次数,又为了不影响前面的子区间,我们考虑改变本段。考虑将本段的子段的累计先赋值成当前已经记录的数量,再把目标加上这个值,我们就优雅的记录了这个数。而在区间求和的时候就可以得到一种优雅的写法。
对于每次同步我们可以用如下代码。
val[k] -= sum[k] - tmp[k] , tmp[k] = sum[k]
即每次把还未同步的部分加到总和里,再同步数量。
对于每一次闹鬼,就是把输入数的所有质因子(也就是一个子区间)减去上权值,如果这时此区间将为 $0$ 及以下,则就可能得到答案,或者需要重新分配子区间的值。
当然这里不用全部枚举,我们可以用个 ds 维护一下使要求的数量从小到大排序,当出现不成立时后面的一定不成立就可以退出了。
赋值时有一个细节,我们可以直接赋值上取整。
证明:
设:一个数 $x$ 有 $k$ 个质因子权值为 $sum$。
若 $x \mid k$,
每个质因子权值为 $ \frac {sum} {k}$,
根据鸽笼原理,最小的最大值为 $\frac {sum} {k}$ 符合。
若 $x \nmid k$,
每个质因子权值最大为 $\frac {sum} {k + 1}$,
根据鸽笼原理,最小的最大值为 $\frac {sum} {k + 1}$ 符合。
另外不要忘了“真实的 $y = y' \bigoplus LastAns$”。
这样你就可以把这道题切掉了。
Code
本质和第一篇题解没有区别,但是传送门[Link]。
标签:鬼街,frac,每个,sum,因子,权值,区间,THUPC2021,P7603 From: https://www.cnblogs.com/xztx666/p/17363907.html