通常是一维数组，要寻找任一个元素的右边或者左边第一个比自己大或者小的元素的位置，此时我们就要想到可以用单调栈了

739. 每日温度

题目说明

请根据每日气温列表，重新生成一个列表。对应位置的输出为：要想观测到更高的气温，至少需要等待的天数。如果气温在这之后都不会升高，请在该位置用 0 来代替。

例如，给定一个列表 temperatures = [73, 74, 75, 71, 69, 72, 76, 73]，你的输出应该是 [1, 1, 4, 2, 1, 1, 0, 0]。

提示：气温列表长度的范围是 [1, 30000]。每个气温的值的均为华氏度，都是在 [30, 100] 范围内的整数。

解题思路

利用单调栈的思路，如果出现了比一个数大的值，则记录下这个值，找到了答案。如果没有找到的话，则在栈中维护单调递减情况（从栈底到栈头），因为为了确定某一位置的答案是多少，所以栈中存储的是数组的下标。

因为新的元素可能比栈中的都大，所以要反复的用栈头元素去和当前的元素比较，直到栈为空或者新元素比栈头元素小或相等为止（保证单调）

核心逻辑如下：

for (int i = 0; i < temperatures.length; i++) {
    while (!stack.isEmpty()) {
        if (temperatures[stack.peek()] < temperatures[i]) {
            res[stack.peek()] = i - stack.peek();
            stack.pop();
        } else {
            break;
        }
    }
    stack.push(i);
}

496.下一个更大元素 I

题目说明

给你两个 没有重复元素 的数组 nums1 和 nums2 ，其中nums1 是 nums2 的子集。

请你找出 nums1 中每个元素在 nums2 中的下一个比其大的值。

nums1 中数字 x 的下一个更大元素是指 x 在 nums2 中对应位置的右边的第一个比 x 大的元素。如果不存在，对应位置输出 -1 。

示例 1:

输入: nums1 = [4,1,2], nums2 = [1,3,4,2].
输出: [-1,3,-1]
解释:
对于 num1 中的数字 4 ，你无法在第二个数组中找到下一个更大的数字，因此输出 -1 。
对于 num1 中的数字 1 ，第二个数组中数字1右边的下一个较大数字是 3 。
对于 num1 中的数字 2 ，第二个数组中没有下一个更大的数字，因此输出 -1 。

示例 2:
输入: nums1 = [2,4], nums2 = [1,2,3,4].
输出: [3,-1]
解释:
对于 num1 中的数字 2 ，第二个数组中的下一个较大数字是 3 。
对于 num1 中的数字 4 ，第二个数组中没有下一个更大的数字，因此输出-1 。

提示：

• 1 <= nums1.length <= nums2.length <= 1000
• 0 <= nums1[i], nums2[i] <= 10^4
• nums1和nums2中所有整数 互不相同
• nums1 中的所有整数同样出现在 nums2 中

解题思路

和739. 每日温度相似的是，找出每个值后面第一个比他大的值，如果不同的话则赋-1。不同之处在于，本题不是求所有元素比他大的值，而是求所有元素的子集（打乱顺序）后面的比他大的值，此处问题可以通过一个HashMap映射来解决。

同样维护一个单调栈来遍历数组，从栈底到栈顶维持一个单调递减的顺序。不断将新元素于栈顶元素进行一个比较，此处栈不需要记录元素的下标，因为只要获得值后面的第一个更大值即可，并将(stack.pop(), nums2[i])存入HashMap中。

由以上方式获得的HashMap一定不包含所有元素（总会有值后面没有更大值），因此在nums1中取值的时候可以通过map.getOrDefault(nums1[i], -1)的方式来解决

503.下一个更大元素II

题目说明

给定一个循环数组（最后一个元素的下一个元素是数组的第一个元素），输出每个元素的下一个更大元素。数字 x 的下一个更大的元素是按数组遍历顺序，这个数字之后的第一个比它更大的数，这意味着你应该循环地搜索它的下一个更大的数。如果不存在，则输出 -1。

示例 1:

• 输入: [1,2,1]
• 输出: [2,-1,2]
• 解释: 第一个 1 的下一个更大的数是 2；数字 2 找不到下一个更大的数；第二个 1 的下一个最大的数需要循环搜索，结果也是 2。

提示:

• 1 <= nums.length <= 10^4
• -10^9 <= nums[i] <= 10^9

解题思路

和496.下一个更大元素 I的区别在于该数组是循环的，每个数字的下一个最大数值在index上可能比它自己小，因此我们只需要把遍历的范围从nums.length扩大到2 * nums.length - 1，对index与nums.length取余操作即可。

在创建结果数组的时候先对数组要对数组进行初始化，因为如果没有更大的值要记录成-1，所以先Arrays.fill(res, -1)处理。

42. 接雨水

题目说明

给定 n 个非负整数表示每个宽度为 1 的柱子的高度图，计算按此排列的柱子，下雨之后能接多少雨水。

示例 1：

• 输入：height = [0,1,0,2,1,0,1,3,2,1,2,1]
• 输出：6
• 解释：上面是由数组 [0,1,0,2,1,0,1,3,2,1,2,1] 表示的高度图，在这种情况下，可以接 6 个单位的雨水（蓝色部分表示雨水）。

示例 2：

• 输入：height = [4,2,0,3,2,5]
• 输出：9

解题思路1：双指针

双指针法用到的是纵向处理的思维，即水的体积是一列一列进行计算的。那么针对每一个index的底都是一样的（1），不同的只是容器的高度（短板效应）。因此可以对数组进行遍历，获取每个位置的左边最大值和右边最大值，取其小减去容器的底座高度即是容器边缘的高。

// 遍历数组
leftmax[i] = Math.max(leftmax[i - 1], height[i - 1]);
rightmax[i] = Math.max(rightmax[i + 1], height[i + 1]);

最后再遍历一次数组，通过左右及当前位置确定蓄水量加入sum，此时要注意一个，可能出现左边最大值和右边最大值都没有当前位置高的情况，此时是无法蓄水的，记得pass这个位置，否则会加上一个负数。

解题思路2：单调栈

单调栈法用的是横向处理的思想，可以理解为找到一个波谷的位置，然后通过sum把这个波谷可以蓄的水加上去。因此单调栈从栈底到栈头维持一个单调递减的序列，当栈头元素小于当前元素时意味着波谷出现，此时heights[stack.pop()]即为底，heights[stack.peek()]和heights[i]取小值减去底的高度作为边缘高度，i - stack.peek() + 1作为底的宽度，通过((i - left - 1) * (Math.min(height[i], height[left]) - height[mid]))计算出当前河谷蓄水的值。

并且要不断的去和栈头比较除非栈为空，维持单调递减的顺序，不断对新生成的河谷去计算蓄水量while (!stack.isEmpty() && height[stack.peek()] < height[i]){}。

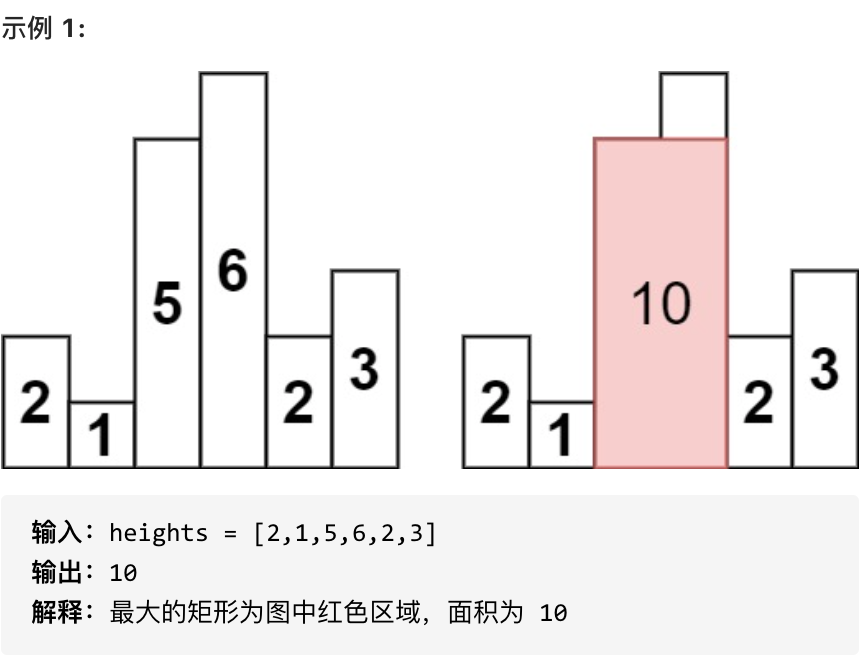
84.柱状图中最大的矩形

给定 n 个非负整数，用来表示柱状图中各个柱子的高度。每个柱子彼此相邻，且宽度为 1 。

求在该柱状图中，能够勾勒出来的矩形的最大面积。

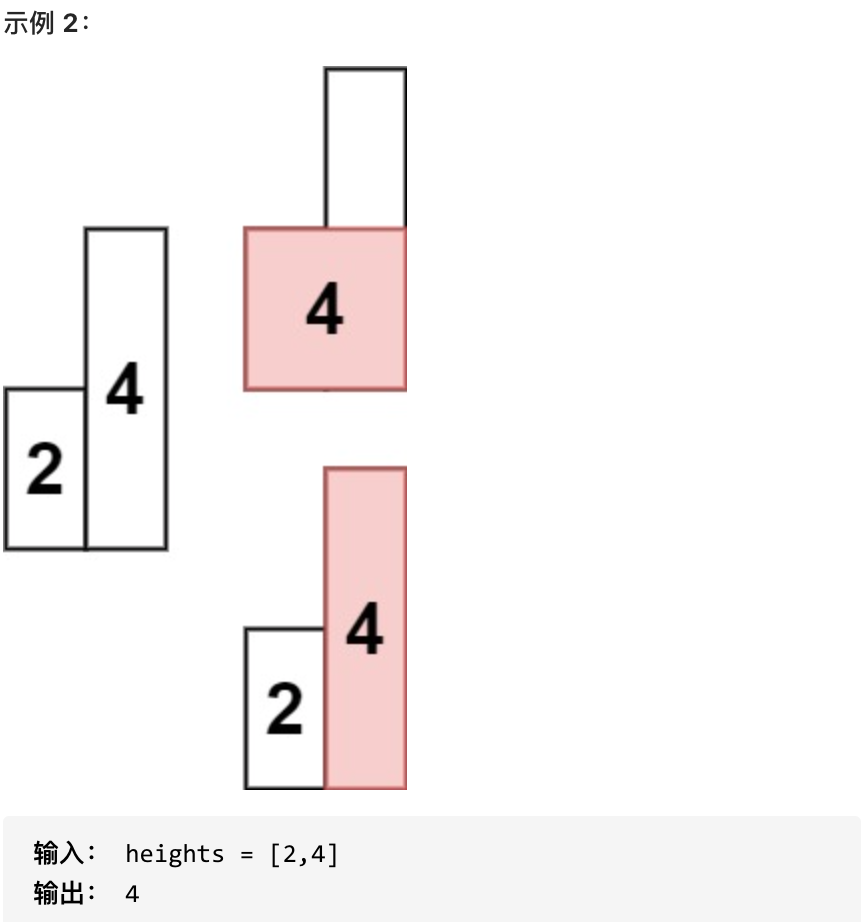
• 1 <= heights.length <=10^5
• 0 <= heights[i] <= 10^4

解题思路1：单调栈

此题需要确定，当什么时候需要把栈头的元素弹出来计算基于栈头元素作为高构成的矩形的面积的最大值。因此考虑从栈底到栈头维护一个递增序列还是递减序列。如果维护一个递减序列，无法确定以当前位置作为高时，左右两端的位置在哪里（左端一定在栈底，右端可能还未出现），因此决定维护一个递增的序列。

维护递增序列的好处是，以stack.pop()的值作为高的话，用遍历到的 i 减去pop之后的stack.peek() + 1，可以保证这一段序列都是以stack.pop()作为高的，底乘高即可获得面积。通过不断的和栈顶去比较即可维护单调递增的序列不断求的以当前高度作为高的面积。

除此之外，因为第一个元素和最后一个元素也需要处理。因此要在0号元素前面加上一个0号位用于保证第一个元素可以被计算，在最后一个元素后面再加入一个0来保证最后一个元素可以被计算。

因此可以创建一个新的数组int[] newHeights = new int[heights.length + 2];，头尾置零即可。

解题思路2：双指针

双指针的思路同样是要找到以当前元素作为高时，左右两边第一个比它低的元素的位置。由此可以确定该元素做高时最大的底是多少。此时需要对left[]和right[]两边进行初始化，left[0]应置为-1，right[right.length - 1]应置为right.length，理解为左右第一个位置即可（也只能是这两个值了）。

当最大值还未出现时，可以通过令index = left[index]和index = right[index]提高找到目标值的速度（不用一个个去遍历）。

获取到left数组和right数组后，即可遍历高度数组来更新max值，并返回最终结果。