题目1：

题意

• 有 \(2n\) 个点，\(3n - 2\) 条边的无向图，对于 \(i(1 \le i \le n)\)，\(i, i + n\) 连边，并且对于 \(i(1 \le i \le n - 1)\)，\(i, i + 1\) 以及 \(i + n, i + n + 1\) 连边。问对与 \(i = 1, 2, 3, \dots, n - 1\)，有几种删 \(i\) 条的边方式使图连通, 答案对质数 \(mod\) 取模。

• \(1 \le n \le 3005\)。

思路

• 首先我们先不考虑栅极条边的方案数，先想有几种删边方案是的图连通。

• 我们先只考虑前 \(i\) 列，如果前 \(i\) 列不连通，则上下两排不连通的一定是一段后缀，否则就永远无法连通了，也就是非法的。

• 所以我们需要考虑前 \(i\) 列连通和不连通的方案数（不连通一定合法）。左右图展示了 \(8\) 种情况，左边是第 \(i - 1\) 列，右边是第 \(i\) 列，第 \(i - 1\) 列的两个点是否连边表示两个点是否连通。左图是选完边后前 \(i\) 列连通的情况，右图为不连通（右图为合法的）。

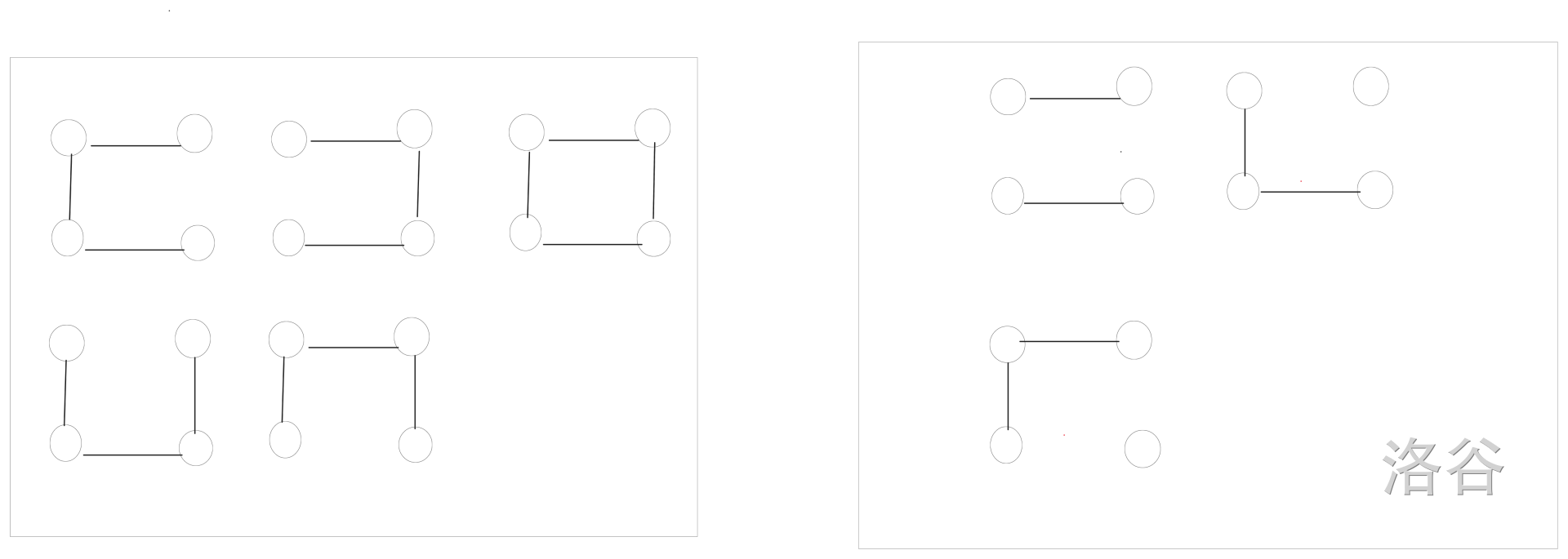
• 可以发现列从小到大，状态是转移都出来了 （状态：前 \(i\) 列连通和不连通的方案数（合法），转移就在上图），那不就是 \(dp\) 吗？

• 现在我么回归正轨，题目是问有几种删 \(i\) 条的边方式使图连通，那该怎么办了？其实就是多开一维状态 \(dp_{i, j, k}\) 表示前 \(i\) 列删边 \(j\) 条使前 \(i\) 列连通或不连通的方案数，转移就是：

dp[i][j][1] = (dp[i - 1][j - 1][1] * 3 + dp[i - 1][j][1] + dp[i - 1][j][0]) % mod;
dp[i][j][0] = (dp[i - 1][j - 1][0] + (j > 1 ? dp[i - 1][j - 2][1] * 2 : 0)) % mod;

• 初始状态：\(dp_{1, 1, 0} = 1, dp_{1, 0, 1} = 1\)，目标状态：\(dp_{n, 1, 1}, dp_{n, 2, 1}, \dots dp_{n, n - 1,1}\)。

• 时间复杂度：状态数：\(O(n^2)\)，转移数：\(O(n^2)\)，总时间复杂度：\(O(n^2)\)。

const int MAXN = 3005;

int n, mod;
long long dp[MAXN][MAXN][2];

int main() {
  ios::sync_with_stdio(0), cin.tie(0);
  cin >> n >> mod;
  dp[1][0][1] = 1, dp[1][1][0] = 1;
  for (int i = 2; i <= n; i++) {
    dp[i][0][1] = 1;
    for (int j = 1; j < n; j++) {
      dp[i][j][1] = (dp[i - 1][j - 1][1] * 3 + dp[i - 1][j][1] + dp[i - 1][j][0]) % mod;
      dp[i][j][0] = (dp[i - 1][j - 1][0] + (j > 1 ? dp[i - 1][j - 2][1] * 2 : 0)) % mod;
    }
  }
  for (int i = 1; i < n; i++) {
    cout << dp[n][i][1] << ' ';
  }
  return 0;
}