原文:Hands-On Convolutional Neural Networks with TensorFlow
译者:飞龙
本文来自【ApacheCN 深度学习 译文集】,采用译后编辑(MTPE)流程来尽可能提升效率。
不要担心自己的形象,只关心如何实现目标。——《原则》,生活原则 2.3.c
一、TensorFlow 的设置和介绍
TensorFlow 是 Google 创建的开源软件库,可让您构建和执行数据流图以进行数值计算。 在这些图中,每个节点表示要执行的某些计算或功能,连接节点的图边表示它们之间流动的数据。 在 TensorFlow 中,数据是称为张量的多维数组。 张量围绕图流动,因此命名为 TensorFlow。
机器学习(ML)模型,例如卷积神经网络,可以用这些图表示,而这正是 TensorFlow 最初设计的目的。
在本章中,我们将介绍以下主题:
- 了解 TensorFlow 的思维方式
- 设置和安装 TensorFlow
- TensorFlow API 级别简介
- 在 TensorFlow 中构建和训练线性分类器
- 评估训练好的模型
TensorFlow 的思维方式
使用 TensorFlow 所需的编程方法与您可能习惯使用的方法略有不同,因此让我们探究有什么不同之处。
所有 TensorFlow 程序的核心都有两个主要部分:
- 构造称为
tf.Graph的计算图 - 使用
tf.Session运行计算图
在 TensorFlow 中,计算图是安排成图结构的一系列 TensorFlow 操作。 TensorFlow 图包含两种主要类型的组件:
- 操作:更通常称为 ops,这些是图中的节点。 操作执行需要在图中进行的任何计算。 通常,它们消耗并产生张量。 一些操作很特殊,运行时可能会有某些副作用。
- 张量:这是图的边; 它们将节点连接起来并表示流经节点的数据。 大多数 TensorFlow 操作将产生并消耗这些
tf.Tensors。
在 TensorFlow 中,您使用的主要对象称为张量。 张量是向量和矩阵的一般化。 即使向量是一维的,矩阵是二维的,张量也可以是n维。 TensorFlow 将张量表示为用户指定数据类型的n维数组,例如float32。
TensorFlow 程序通过首先构建计算图来工作。 该图将产生一些tf.Tensor输出。 要求值此输出,您必须通过在输出张量上调用tf.Session.run来在tf.Session中运行它。 当您执行此操作时,TensorFlow 将执行图中需要执行的所有部分,以评估您要求其运行的tf.Tensor。
设置和安装 TensorFlow
TensorFlow 在最新版本的 Ubuntu 和 Windows 上受支持。 Windows 上的 TensorFlow 仅支持使用 Python3,而在 Ubuntu 上使用则允许同时使用 Python2 和 3。我们建议使用 Python3,这就是本书中用于代码示例的内容。
您可以通过多种方式在系统上安装 TensorFlow,这里我们将介绍两种主要方式。 最简单的方法就是使用 PIP 软件包管理器。 从终端发出以下命令会将 TensorFlow 的仅 CPU 版本安装到您的系统 Python 中:
$ pip3 install --upgrade tensorflow
要安装支持使用您的 Nvidia GPU 的 Tensorflow 版本,只需键入以下内容:
$ pip3 install --upgrade tensorflow-gpu
TensorFlow 的优势之一是它允许您编写可以直接在 GPU 上运行的代码。 除了少数例外,TensorFlow 中的几乎所有主要操作都可以在 GPU 上运行以加快其执行速度。 我们将看到,这对于训练本书稍后描述的大型卷积神经网络将至关重要。
Conda 环境
使用 PIP 可能是上手最快的方法,但是我发现最方便的方法是使用 conda 环境。
Conda 环境允许您创建隔离的 Python 环境,该环境与系统 Python 或任何其他 Python 程序完全独立。 这样一来,您的 TensorFlow 安装就不会与已经安装的任何内容发生混乱,反之亦然。
要使用 conda,您必须从此处下载 Anaconda。 这将包括 conda。 一旦安装了 Anaconda,即可通过在命令提示符中输入某些命令来完成 TensorFlow 的安装。 首先,输入以下内容:
$ conda create -n tf_env pip python=3.5
这将创建名称为tf_env的 conda 环境,该环境将使用 Python 3.5,并且还将安装pip供我们使用。
创建此环境后,您可以通过在 Windows 上输入以下内容来开始使用它:
$ activate tf_env
如果您使用的是 Ubuntu,请输入以下命令:
$ source activate tf_env
现在,它应该在命令提示符旁边显示(tf_env)。 要安装 TensorFlow,我们只需像以前一样进行点安装,具体取决于您是否仅需要 CPU 还是需要 GPU 支持:
(tf_env)$ pip install --upgrade tensorflow
(tf_env)$ pip install --upgrade tensorflow-gpu
检查您的安装是否正常
现在您已经安装了 TensorFlow,让我们检查一下它是否正常运行。 在命令提示符中,如果尚未激活环境,请再次激活它,然后输入以下命令来运行 Python:
(tf_env)$ python
现在,在 Python 解释器中输入以下行以测试 TensorFlow 是否已正确安装:
>>>> import tensorflow as tf
>>>> x = tf.constant('Tensorflow works!')
>>>> sess = tf.Session()
>>>> sess.run(x)
如果一切都正确安装,您应该看到以下输出:
**b'Tensorflow works!'**
您刚刚输入的是 TensorFlow 的Hello World。 您创建了一个包含单个tf.constant的图,该图只是一个常数张量。 将字符串传递给张量时,推断其为字符串类型。 然后,您创建了一个 TensorFlow 会话,这是运行图所必需的,并将您创建的张量上的会话告知run。 然后打印出会话运行的结果。 那里有一个额外的b,因为它是一个字节流。
如果没有看到上述内容并且出现一些错误,则最好的选择是检查以下页面,以获取安装时遇到的常见问题的解决方案:
TensorFlow API 级别
在我们开始编写 TensorFlow 代码之前,了解 TensorFlow 在 Python 中提供的 API 抽象层次的不同很重要。 这样,我们可以了解编写代码时可以使用的功能,还可以为工作选择正确的功能或操作。 很多时候,几乎不需要从头开始重写已经可以在 TensorFlow 中使用的东西。
TensorFlow 提供了三层 API 抽象来帮助编写您的代码,这些可以在下图中可视化:
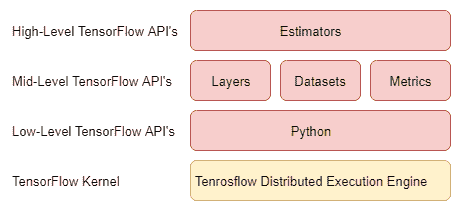
在最低级别上,您具有基本的 TensorFlow 操作,例如tf.nn.conv2d和tf.nn.relu。 使用 TensorFlow 时,这些低级原语为用户提供了最大的控制权。 但是,使用它们的代价是在构造图和编写更多样板代码时必须自己动手做很多事情。
现在不用担心理解以下任何代码示例,我保证很快就会出现。 现在只是在这里展示 TensorFlow 中的不同 API 级别。
因此,例如,如果我们想创建一个卷积层以在我们的 ML 模型中使用,那么它可能类似于以下内容:
def my_conv_2d(input, weight_shape, num_filters, strides):
my_weights = tf.get_variable(name="weights", shape=weight_shape)
my_bias = tf.get_variable(name="bias", shape=num_filters)
my_conv = tf.nn.conv2d(input, my_weights, strides=strides, padding='same', name='conv_layer1')
my_conv = tf.nn.bias_add(my_conv, my_bias)
conv_layer_out = tf.nn.relu(my_conv)
return conv_layer_out
这个示例比您实际实现的简单得多,但是您已经可以看到开始建立代码的行数,以及必须注意的事情,例如构造权重和添加偏置项。 一个模型也将具有许多不同种类的层,而不仅仅是卷积层,所有这些层都必须以与此非常相似的方式来构造。
因此,不仅要为模型中所需的每种新层将这些内容写出来都非常费力,而且还引入了更多的区域,在这些区域中,错误可能会潜入您的代码中,这从来都不是一件好事。
对我们来说幸运的是,TensorFlow 具有第二层抽象,可以帮助您简化构建 TensorFlow 图时的工作。 这种抽象级别的一个示例是层 API。 层 API 使您可以轻松处理许多机器学习任务中常见的许多构建基块。
层 API 的工作方式是包装我们在上一个示例中编写的所有内容并将其抽象出来,因此我们不必再为它担心。 例如,我们可以压缩前面的代码以将卷积层构造为一个函数调用。 与以前建立相同的卷积层现在看起来像这样:
def my_conv_2d(input, kernel_size, num_filters, strides):
conv_layer_out = tf.layers.conv2d(input, filters=num_filters, kernel_size=kernel_size, strides=strides, padding='same', activation=tf.nn.relu, name='conv_layer1')
return conv_layer_out
还有两个与各层一起工作的 API。 第一个是数据集 API,可轻松将数据加载和馈送到 TensorFlow 图。 第二个是指标 API,它提供工具来测试您训练有素的机器学习模型的运行状况。 我们将在本书的后面部分中学习所有这些内容。
API 栈的最后一层是 TensorFlow 提供的最高抽象层,这称为估计器 API。 就像使用tf.layers来构造权重并为单个层添加偏差一样,估计器 API 封装了许多层的结构,以便我们可以将一个由多个不同层组成的整体模型定义为一个函数调用。
本书不会介绍估计器 API 的用法,但是如果读者希望了解有关估计器的更多信息,可以在 TensorFlow 网站上找到一些有用的教程。
本书将重点介绍如何使用低级 API 以及层,数据集和指标 API 来构建,训练和评估自己的 ML 模型。 我们相信,通过使用这些较低级别的 API,读者将对 TensorFlow 的幕后工作方式有更深入的了解,并有能力更好地应对可能需要使用这些较低级别 API 的各种未来问题。
急切执行
在撰写本文时,Google 刚刚将急切的执行 API 引入了 TensorFlow。 急切执行是 TensorFlow 对另一个名为 PyTorch 的深度学习库的回答。 它允许您绕过通常的 TensorFlow 工作方式,在这种方式下,您必须首先定义计算图,然后执行该图以获得结果。 这称为静态图计算。 相反,现在您可以使用急切执行创建在运行程序时动态定义的所谓动态图。 使用 TensorFlow 时,这允许使用更传统的命令式编程方式。 不幸的是,急切的执行仍在开发中,缺少某些功能,因此在本书中不作介绍。 可以在 TensorFlow 网站上找到有关急切执行的更多信息。
建立您的第一个 TensorFlow 模型
事不宜迟,让我们开始在 TensorFlow 中构建您的第一个 ML 模型。
我们将在本章中解决的问题是从四个给定的特征值正确识别鸢尾花的种类。 这是一个非常容易解决的经典 ML 问题,但它将为我们提供一种很好的方式来介绍在 TensorFlow 中构建图,馈送数据和训练 ML 模型的基础知识。
鸢尾数据集由 150 个数据点组成,每个数据点具有四个相应的特征:长度,花瓣宽度,萼片长度和萼片宽度以及目标标签。 我们的任务是建立一个模型,仅给出这四个特征就可以推断出任何鸢尾的目标标签。
让我们开始加载数据并进行处理。 TensorFlow 具有内置功能,可以为我们导入此特定数据集,因此让我们继续使用它。 由于我们的数据集很小,因此将整个数据集加载到内存中是可行的。 但是,不建议将其用于较大的数据集,并且在接下来的章节中,您将学到更好的处理此问题的方法。 以下代码块将为我们加载数据,然后对其进行解释。
import tensorflow as tf
import numpy as np
# Set random seed for reproducibility.
np.random.seed(0)
data, labels = tf.contrib.learn.datasets.load_dataset("iris")
num_elements = len(labels)
# Use shuffled indexing to shuffle dataset.
shuffled_indices = np.arange(len(labels))
np.random.shuffle(shuffled_indices)
shuffled_data = data[shuffled_indices]
shuffled_labels = labels[shuffled_indices]
# Transform labels into one hot vectors.
one_hot_labels = np.zeros([num_elements,3], dtype=int)
one_hot_labels[np.arange(num_elements), shuffled_labels] = 1
# Split data into training and testing sets.
train_data = shuffled_data[0:105]
train_labels = shuffled_labels[0:105]
test_data = shuffled_data[105:]
test_labels = shuffled_labels[105:]
让我们再次看一下这段代码,看看到目前为止我们做了什么。 导入 TensorFlow 和 Numpy 之后,我们将整个数据集加载到内存中。 我们的数据由表示为向量的四个数值特征组成。 我们总共有 150 个数据点,因此我们的数据将是形状为150 x 4的矩阵,其中每一行代表不同的数据点,每一列代表不同的特征。 每个数据点还具有与之关联的目标标签,该目标标签存储在单独的标签向量中。
接下来,我们重新整理数据集; 这一点很重要,因此,当我们将其分为训练集和测试集时,我们在这两个集之间平均分配,并且最终不会在一组集中获得所有一种类型的数据。
单热向量
改组后,我们对数据标签进行一些预处理。 随数据集加载的标签只是一个 150 长度的整数向量,表示每个数据点所属的目标类,在这种情况下为 1、2 或 3。 在创建机器学习模型时,我们希望将标签转换为一种新的形式,通过执行一种称为“单热编码”的方式可以更轻松地使用它。
不是使用单个数字作为每个数据点的标签,而是使用向量。 每个向量将与您拥有的不同目标类别的数目一样长。 因此,例如,如果您有 5 个目标类,则每个向量将有 5 个元素;例如, 如果您有 1,000 个目标类别,则每个向量将具有 1,000 个元素。 向量中的每一列代表我们的目标类别之一,我们可以使用二进制值来确定向量是其标签的类别。 可以通过将所有值设置为 0 并将 1 放入我们希望向量标签表示的类的列中来完成。
用一个例子很容易理解。 对于这个特定问题的标签,转换后的向量将如下所示:
1 = [1,0,0]
2 = [0,1,0]
3 = [0,0,1]
分为训练和测试集
最后,我们将数据集的一部分放到一边。 这就是我们的测试集,在我们训练模型之后我们才接触它。 该集合用于评估我们训练有素的模型对从未见过的新数据的表现。 有许多方法可以将数据分为训练集和测试集,我们将在本书的后面详细介绍它们。
但就目前而言,我们将进行一个简单的 70:30 拆分,因此我们仅使用总数据的 70% 来训练我们的模型,然后对剩余的 30% 进行测试。
创建 TensorFlow 图
现在我们的数据都已经设置好了,我们可以构建模型来学习如何对鸢尾花进行分类。 我们将构建最简单的机器学习模型之一-线性分类器,如下所示:

线性分类器通过计算输入特征向量x和权重向量w之间的点积来工作。 在计算出点积之后,我们向结果添加一个值,称为偏差项b。 在我们的例子中,我们有三种可能的类别,任何输入特征向量都可能属于该类别,因此我们需要使用w[1],w[2]计算三种不同的点积,w[3]以查看其属于哪个类别。 但是,我们不必写出三个单独的点积,而只需在形状[3, 4]的权重矩阵与输入向量之间做一个矩阵乘法。 在下图中,我们可以更清楚地看到它的外观:
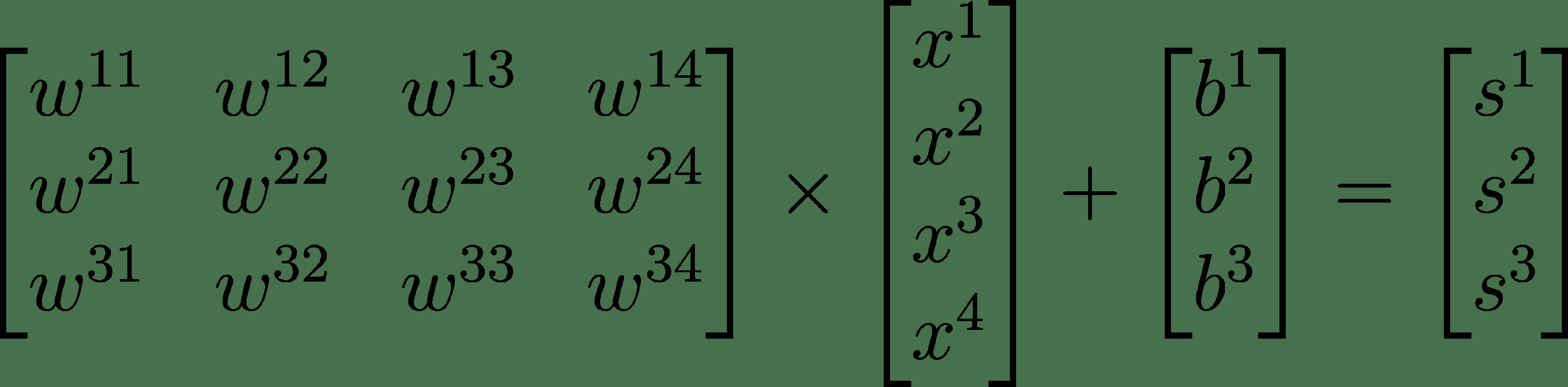
我们还可以将该方程简化为更紧凑的形式,如下所示,其中我们的权重矩阵为W,偏差为b,x是我们的输入特征向量,结果输出为s:

变量
我们如何在 TensorFlow 代码中全部写出来? 让我们开始创建权重和偏置。 在 TensorFlow 中,如果我们想创建一些可以被我们的代码操纵的张量,那么我们需要使用 TensorFlow 变量。 TensorFlow 变量是tf.Variable类的实例。 tf.Variable类表示tf.Tensor对象,可以通过在其上运行 TensorFlow 操作来更改其值。 变量是类似于张量的对象,因此它们可以以与张量相同的方式传递,并且可以与张量一起使用的任何操作都可以与变量一起使用。
要创建变量,我们可以使用tf.get_variable()。 调用此函数时,必须提供变量的名称。 此函数将首先检查图上是否没有其他具有相同名称的变量,如果没有,则它将创建新变量并将其添加到 TensorFlow 图。
您还必须指定变量要具有的形状,或者,可以使用tf.constant张量来初始化变量。 变量将采用您的常数张量的值,并且形状将自动推断。 例如,以下代码将产生一个包含值 21 和 25 的1x2张量:
my_variable = tf.get_variable(name= "my_variable", initializer=tf.constant([21, 25]))
工作方式
在图中有变量很好,但我们也想对它们做点什么。 我们可以使用 TensorFlow 操作来操作我们的变量。
如前所述,我们的线性分类器只是一个矩阵乘法运算,因此您将要使用的第一个运算很有趣地成为矩阵乘法运算。 只需在您要相乘的两个张量上调用tf.matmul(),结果将是您传入的两个张量的矩阵相乘。简单!
在整本书中,您将了解需要使用的许多不同的 TensorFlow 操作。
现在,您希望对变量和操作有所了解,让我们构建线性模型。 我们将在函数中定义模型。 该函数将以 N 个特征向量为输入,或更准确地说,以 N 个大小为一批。由于我们的特征向量的长度为 4,所以我们的批次将是[N, 4]形状张量。 然后该函数将返回线性模型的输出。 在下面的代码中,我们编写了线性模型函数,该函数应该可以自我解释,但是如果您还没有完全理解它,请继续阅读。
def linear_model(input):
# Create variables for our weights and biases
my_weights = tf.get_variable(name="weights", shape=[4,3])
my_bias = tf.get_variable(name="bias", shape=[3])
# Create a linear classifier.
linear_layer = tf.matmul(input, my_weights)
linear_layer_out = tf.nn.bias_add(value=linear_layer, bias=my_bias)
return linear_layer_out
在此处的代码中,我们创建了将存储权重和偏差的变量。 我们给他们起名字并提供所需的形状。 请记住,我们使用变量是因为我们想通过操作来操纵它们的值。
接下来,我们创建一个tf.matmul节点,将我们的输入特征矩阵和权重矩阵作为参数。 可以通过我们的linear_layer Python 变量访问此操作的结果。 然后将该结果传递给另一个运算符tf.nn.bias_add。 该运算来自 NN(神经网络)模块,在我们希望向计算结果中添加偏差向量时使用。 偏差必须是一维张量。
使用占位符馈送数据
占位符是类似张量的对象。 它们是您与 TensorFlow 之间的合同,该合同规定,当您在会话中运行计算图时,您将提供数据或将数据馈入该占位符,以便您的图可以成功运行。
它们就像张量一样,就像张量一样,意味着您可以将它们传递到放置张量的地方。
通过使用占位符,我们可以向图中提供外部输入,这些输入可能会在每次运行图时更改。 它们的自然用法是将数据和标签提供到模型中的一种方式,因为每次我们要运行图时,我们提供的数据和标签通常都会有所不同。
创建占位符时,我们必须提供将要填充的数据类型。
我们将使用两个占位符将数据和标签提供到图中。 我们还提供了馈入这些占位符的任何数据都必须采用的形状。 我们使用None表示该特定尺寸的大小可以为任何值。 这样,我们就可以批量输入大小不同的数据。 接下来,我们将看到如何在 TensorFlow 中为我们的问题定义占位符。
x = tf.placeholder(tf.float32, shape=[None, 4], name="data_in")
y = tf.placeholder(tf.int32, shape=[None, 3], name="target_labels")
现在,我们在图中创建了占位符,因此我们也可以在图上构造线性模型。 我们调用之前定义的函数,并提供数据占位符x作为输入。 请记住,占位符的行为类似于张量,因此它们也可以像它们一样被传递。 在以下代码中,我们使用占位符作为输入参数来调用linear_model函数。
model_out = linear_model(x)
当我们调用函数时,函数中的所有内容都会执行,所有操作和变量都将添加到 TensorFlow 图中。 我们只需要这样做一次。 如果我们再次尝试调用函数,则会收到一条错误消息,说明我们已尝试向图添加变量,但变量已经存在。
占位符是向我们的图中提供外部数据的最简单,最快的方法,因此很高兴了解它们。 稍后,我们将看到使用数据集 API 提供数据的更好方法,但是就目前而言,占位符是一个不错的起点。
初始化变量
在我们能够在图中使用变量之前,我们必须对其进行初始化。 我们需要创建一个图节点来为我们做到这一点。 使用tf.global_variables_initializer将向我们的图添加一个初始化器节点。 如果我们在会话中运行该节点,那么图中的所有变量都将被初始化,以便我们可以使用它们。 因此,现在,让我们创建一个初始化器节点,如下所示:
initializer = tf.global_variables_initializer()
正如我们没有明确说明要对变量使用哪种初始化一样,TensorFlow 将使用默认的一种称为 Glorot 正态初始化的方法,也称为 Xavier 初始化。
训练我们的模型
我们已经构建了线性模型的图,并且可以向其中提供数据。 如果我们创建一个会话并在提供一些输入数据的同时运行model_out张量,那么我们将得到一个结果。 但是,我们得到的输出将完全是垃圾。 我们的模型尚未训练! 当我们使用初始化节点初始化变量时,权重和偏差的值仅具有默认值。
损失函数
要训练我们的模型,我们必须定义一些称为损失函数的函数。 损失函数将告诉我们我们的模型目前做得如何好坏。
损失可在tf.losses模块中找到。 对于此模型,我们将使用铰链损失。 铰链损失是创建支持向量机(SVM)时使用的损失函数。 铰链损失严重惩罚了错误的预测。 对于一个给定的示例(x[i], y[i]),其中x[i]是数据点的特征向量,y[i]是其标记,其铰链损失如下:

为此,以下内容将适用:
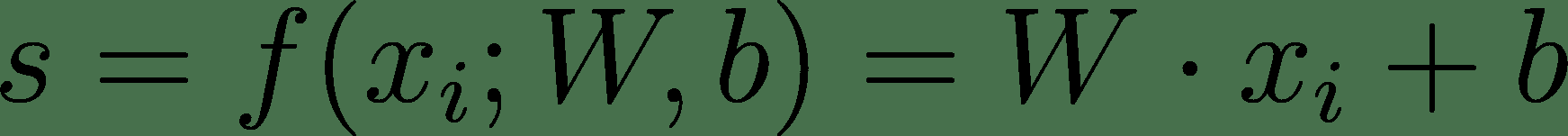
简而言之,该方程式采用分类器的原始输出。 在我们的模型中,这是三个输出分数,并确保目标类别的分数至少比其他类别的分数大至少 1。 对于每个分数(目标类别除外),如果满足此限制,则将损失加 0,否则,将增加罚款:

这个概念实际上是非常直观的,因为如果我们的权重和偏置得到了正确的训练,那么所产生的三个得分中的最高得分就可以自信地表明输入示例所属的正确类别。
由于在训练期间,我们会一次输入许多训练示例,因此,我们将获得多个需要平均的损失。 因此,需要最小化的总损失方程如下:
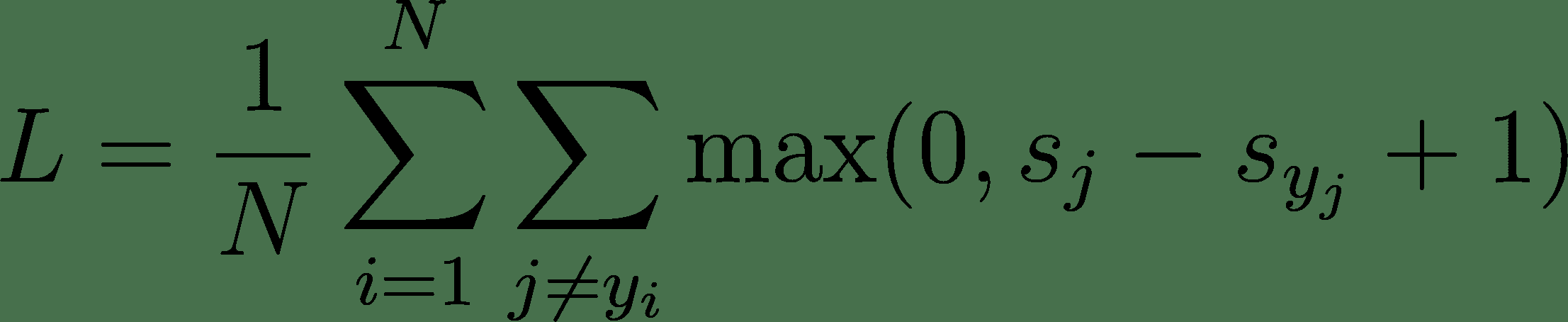
在我们的代码中,损失函数将带有两个参数:logits和label。 在 TensorFlow 中,logits是我们的模型产生的原始值的名称。 在我们的例子中,这是model_out,因为这是我们模型的输出。 对于标签,我们使用标签占位符y。 请记住,占位符将在运行时为我们填充:
loss = tf.reduce_mean(tf.losses.hinge_loss(logits=model_out, labels=y))
由于我们也想对整个输入数据的损失进行平均,因此我们使用tf.reduce_mean将所有损失平均为一个损失值,将其最小化。
有许多不同类型的损失函数可供我们使用,这些函数对于不同的机器学习任务都是有益的。 在阅读本书时,我们将学习更多这些内容以及何时使用不同的损失函数。
优化
现在我们定义了要使用的损失函数; 我们可以使用这个损失函数来训练我们的模型。 如前面的方程式所示,损失函数是权重和偏差的函数。 因此,我们要做的就是详尽地搜索权重和偏差的空间,并查看哪种组合最大程度地减少了损失。 当我们具有一维或二维权向量时,此过程可能还可以,但是当权向量空间太大时,我们需要一个更有效的解决方案。 为此,我们将使用一种名为梯度下降的优化技术。
通过使用损失函数和演算,梯度下降法可以看到如何调整模型权重和偏差的值,以使损失值减小。 这是一个迭代过程,需要多次迭代才能针对我们的训练数据对权重和偏差的值进行适当调整。 这个想法是,通过相对于目标函数ᐁ[w]L(w)的梯度的相反方向更新参数,可以最小化由权重w参数化的损失函数L。 权重和偏差的更新功能如下所示:

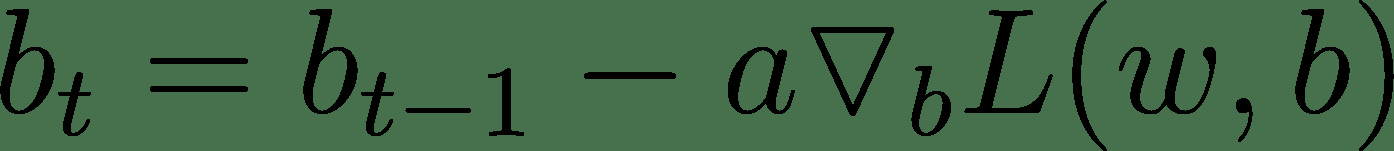
在这里,t是迭代次数,α是称为学习率的超参数。
由两个变量w1和w2参数化的损失函数将如下图所示:
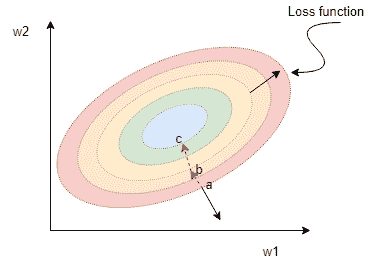
上图显示了椭圆抛物面的水平曲线。 这是一个碗形的表面,碗的底部位于中心。 从图中可以看出,在点a(黑色直箭头)处的梯度向量垂直于通过a的水平曲线。 实际上,梯度向量指向损失函数最大增加率的方向。
因此,如果我们从点开始并朝与相反的方向将权重更新为梯度向量,那么我们将下降至b点,然后在下一次迭代到c,依此类推,直到达到最小值。 选择使损失函数最小的参数来表示最终的训练线性模型。
TensorFlow 的好处在于,它使用其内置的优化器(称为自动微分)为我们计算了所有所需的梯度。 我们要做的就是选择一个梯度下降优化器,并告诉它最小化我们的损失函数。 TensorFlow 将自动计算所有梯度,然后使用这些梯度为我们更新权重。
我们可以在tf.train模块中找到优化程序类。 现在,我们将使用GradientDescentOptimizer类,它只是基本的梯度下降优化算法。 创建优化器时,我们必须提供学习率。 学习率的值是hyperparameter,用户必须通过反复试验和实验来对其进行调整。 0.5 的值应该可以很好地解决此问题。
优化器节点具有一种称为minimize的方法。 在您提供的损失函数上调用此方法会做两件事。 首先,针对您的整个图计算与该损失有关的梯度。 其次,这些梯度用于更新所有相关变量。
创建我们的优化器节点将如下所示:
optimizer = tf.train.GradientDescentOptimizer(learning_rate=0.5).minimize(loss)
与损失函数一样,有很多不同的梯度下降优化器需要学习。 这里介绍的是最基本的一种,但是再次,我们将在以后的章节中学习和使用不同的类型。
评估训练好的模型
我们汇总了训练模型所需的所有零件。 开始训练之前的最后一件事是,我们想在图中创建一些节点,这些节点将使我们能够在完成训练后测试模型的执行情况。
我们将创建一个节点来计算模型的准确率。
Tf.equal将返回一个布尔列表,指示两个提供的列表在哪里相等。 在找到最大值的索引之后,在这种情况下,我们的两个列表将是模型的标签和输出:
correct_prediction = tf.equal(tf.argmax(model_out,1), tf.argmax(y,1))
然后,我们可以再次使用reduce_mean来获得正确预测的平均数量。 不要忘记将我们的boolean correct_prediction列表投射回float32:
accuracy = tf.reduce_mean(tf.cast(correct_prediction, tf.float32))
会话
现在,我们已经构造了计算图的所有部分。 我们需要做的最后一件事是创建一个tf.Session并运行我们的图。 TensorFlow 会话是一种将用 Python 编写的 TensorFlow 程序与为 TensorFlow 供电的 C++ 运行时连接的一种方式。 该会话还使 TensorFlow 可以访问本地或远程计算机上存在的设备,例如 CPU 和 GPU。 另外,该会话将缓存有关构造图的信息,因此可以有效地多次运行计算。
创建会话的标准方法是使用 Python 上下文管理器:with语句块:
with tf.Session() as sess:.
原因是创建会话时,它可以控制计算机上的 CPU,内存和 GPU 资源。 使用完会话后,您希望再次释放所有这些资源,最简单的方法是使用with语句来确保这一点。
创建会话后,我们要做的第一件事是运行初始化器操作。 通过在要评估的图对象上调用tf.Session.run,可以使用会话来求值图中的节点和张量。 当您将图的一部分提供给session.run时,TensorFlow 将在整个图中进行工作,求值所提供的图部分所依赖的所有内容以产生结果。
因此,在我们的示例中,调用sess.run(initializer)将在图中进行搜索,查找执行初始化器所需的所有内容,然后按顺序执行这些节点。 在这种情况下,初始化器节点没有任何连接,因此它将简单地执行一个初始化所有变量的节点。
现在我们的变量已初始化,我们开始训练循环。 我们将训练 1000 个步骤或迭代,因此我们将在其中创建训练步骤的for循环。 训练的步骤数是hyperparameter。 这是我们在训练模型时需要决定的事情。 您可以选择与您选择的值进行权衡,这将在以后的章节中进行讨论。 对于此问题,1000 个步骤将足以获得所需的结果。
我们获取了一批训练数据和标签,并将它们输入到图中。 接下来,我们再次调用session.run。 这次,我们将其称为损失和优化器两件事。 通过将它们放在我们提供给session.run的列表中,我们可以提供想要求值的事物。 TensorFlow 将足够聪明,如果不需要,它不会多次求值图,并且它将重用已经计算出的结果。 我们提供的这个列表称为我们的提取; 它是我们要求值和获取的图中的节点。
在提取列表之后,我们提供了feed_dict或馈送字典。 这是一个字典,其中的每个键都是图中的张量,我们将向该张量输入值(在本例中为占位符),而对应的值就是将被输入到它的值。
session.run的返回值对应于我们的提取列表中的每个值。 我们的第一个获取是图中的损失张量,因此第一个return参数来自此。 第二个获取是优化器节点。 我们不在乎从该节点返回什么,因为我们只在乎优化器节点的计算结果,因此我们将其对应的返回值留空:
with tf.Session() as sess:
sess.run(initializer)
for i in range(1000):
batch_x, batch_y = train_data[:,:], train_labels[:,:]
loss_val, _ = sess.run([loss, optimizer], feed_dict={x : batch_x, y: batch_y})
print("Train Accuracy:", sess.run(accuracy, feed_dict={x: train_data, y: train_labels}))
print("Test Accuracy:", sess.run(accuracy, feed_dict={x: test_data, y: test_labels}))
运行 1000 次迭代后,我们使用另一个session.run调用来获取精度节点的输出。 我们执行两次,一次输入我们的训练数据以获取训练集的准确率,一次输入我们保留的测试数据以获取测试集的准确率。 您应该从0.977778中打印出测试精度,这意味着我们的模型可以正确分类 45 个测试集中的 44 个,一点也不差!
总结
在本章中,我们已经说明了使用 TensorFlow 进行编程的方式以及如何为使用 TensorFlow 设置工作环境。 我们还研究了如何使用 TensorFlow 对鸢尾花朵进行分类来构建,训练和评估自己的线性模型。 在此过程中,我们简要介绍了损失函数和梯度下降优化器。
在下一章中,我们将更多地了解一些关键的深度学习概念,包括卷积神经网络。 我们还将研究如何使用 TensorFlow 来构建和训练深度神经网络。
二、深度学习和卷积神经网络
在开始本章之前,我们需要讨论一下 AI 和机器学习(ML)以及这两个组件如何组合在一起。 术语“人工”是指不真实或自然的事物,而“智能”是指能够理解,学习或能够解决问题的事物(在极端情况下,具有自我意识)。
正式地,人工智能研究始于 1956 年的达特茅斯会议,其中定义了 AI 及其使命。 在接下来的几年中,每个人都很乐观,因为机器能够解决代数问题和学习英语,并且在 1972 年制造了第一台机器人。但是在 1970 年代,由于过分的承诺但交付不足,出现了所谓的 AI 冬季,人工智能研究有限且资金不足。 此后,尽管 AI 通过专家系统重生,但可以显示人类水平的分析技能。 之后,第二次 AI 冬季机器学习在 1990 年代被认可为一个单独的领域,当时概率理论和统计学开始得到利用。
计算能力的提高和解决特定问题的决心促使 IBM 的深蓝的发展在 1997 年击败了国际象棋冠军。 迅速发展,时下的 AI 领域涵盖了许多领域,包括机器学习,计算机视觉,自然语言处理,计划调度和优化,推理/专家系统和机器人技术。
在过去的 10 年中,我们目睹了机器学习和一般 AI 的强大功能。 主要感谢深度学习。
在本章中,我们将涵盖以下主题:
- AI 和 ML 概念的一般说明
- 人工神经网络和深度学习
- 卷积神经网络(CNN)及其主要构建模块
- 使用 TensorFlow 构建 CNN 模型以识别数字图像
- Tensorboard 简介
AI 和 ML
就本书而言,将人工智能(AI)视为计算机科学领域,负责制造可解决特定问题的智能体(软件/机器人)。 在这种情况下,“智能”表示智能体是灵活的,并且它通过传感器感知环境,并将采取使自身在某个特定目标成功的机会最大化的措施。
我们希望 AI 最大化名为期望效用的东西,或者通过执行动作获得某种满足的概率。 一个简单易懂的例子是上学,您将最大程度地获得工作的期望效用。
人工智能渴望取代在完成繁琐的日常任务中涉及的易于出错的人类智能。 AI 旨在模仿(以及智能智能体应该具有)的人类智能的一些主要组成部分是:
- 自然语言处理(NLP):能够理解口头或书面人类语言,并能自然回答问题。 NLP 的一些示例任务包括自动旁白,机器翻译或文本摘要。
- 知识和推理:开发并维护智能体周围世界的最新知识。 遵循人类推理和决策来解决特定问题并对环境的变化做出反应。
- 规划和解决问题的方法:对可能采取的措施进行预测,并选择能最大化预期效用的方案,换句话说,为该情况选择最佳措施。
- 感知:智能体程序所配备的传感器向其提供有关智能体程序所处世界的信息。这些传感器可以像红外传感器一样简单,也可以像语音识别麦克风那样复杂。 或相机以实现机器视觉。
- 学习:要使智能体开发世界知识,它必须使用感知来通过观察来学习。 学习是一种知识获取的方法,可用于推理和制定决策。 AI 的无需处理某些明确编程即可处理从数据中学习算法的子字段,称为机器学习。
ML 使用诸如统计分析,概率模型,决策树和神经网络之类的工具来有效地处理大量数据,而不是人类。
例如,让我们考虑以下手势识别问题。 在此示例中,我们希望我们的机器识别正在显示的手势。 系统的输入是手部图像,如下图所示,输出是它们所代表的数字。 解决该问题的系统需要使用视觉形式的感知。

仅将原始图像作为输入输入到我们的机器将不会产生合理的结果。 因此,应对图像进行预处理以提取某种可解释的抽象。 在我们的特定情况下,最简单的方法是根据颜色对手进行分割,然后进行垂直投影,将x轴上的非零值相加。 如果图像的宽度为 100 像素,则垂直投影将形成一个向量,该向量长 100 个元素(100 维),并且在展开的手指位置具有最高的值。 我们可以将提取的任何特征向量称为特征向量。
假设对于我们的手部数据,我们有 1000 张不同的图像,现在我们已经对其进行处理以提取每个图像的特征向量。 在机器学习阶段,所有特征向量都将被提供给创建模型的机器学习系统。 我们希望该模型能够推广并能够预测未经过系统训练的任何未来图像的数字。
ML 系统的组成部分是评估。 在评估模型时,我们会看到模型在特定任务中的表现。 在我们的示例中,我们将研究它可以多么准确地从图像中预测数字。 90% 的准确率意味着正确预测了 100 张给定图像中的 90 张。 在接下来的章节中,我们将更详细地讨论机器训练和评估过程。
ML 的类型
机器学习问题可以分为三大类,具体取决于我们可以使用哪种数据以及我们想要完成什么:
监督学习:我们可以使用输入和所需的输出或标签。 手势分类是一种有监督学习问题的示例,其中为我们提供了手势和相应标签的图像。 我们想要创建一个模型,该模型能够在输入手形图像的情况下输出正确的标签。
监督技术包括 SVM,LDA,神经网络,CNN,KNN,决策树等。
无监督学习:只有输入可用,没有标签,我们不一定知道我们想要模型做什么。 例如,如果我们得到一个包含手的图片但没有标签的大型数据集。 在这种情况下,我们可能知道数据中存在某些结构或关系,但是我们将其留给算法来尝试在我们的数据中找到它们。 我们可能希望我们的算法在数据中找到相似手势的簇,因此我们不必手动标记它们。
无监督学习的另一种用途是找到方法,以减少我们正在使用的数据的维度,这又是通过找到数据中的重要特征并丢弃不重要的特征来实现的。
无监督技术包括 PCA,t-SNE,K 均值,自编码器,深度自编码器等。
下图说明了分类和聚类之间的区别(当我们需要在非监督数据上查找结构时)。
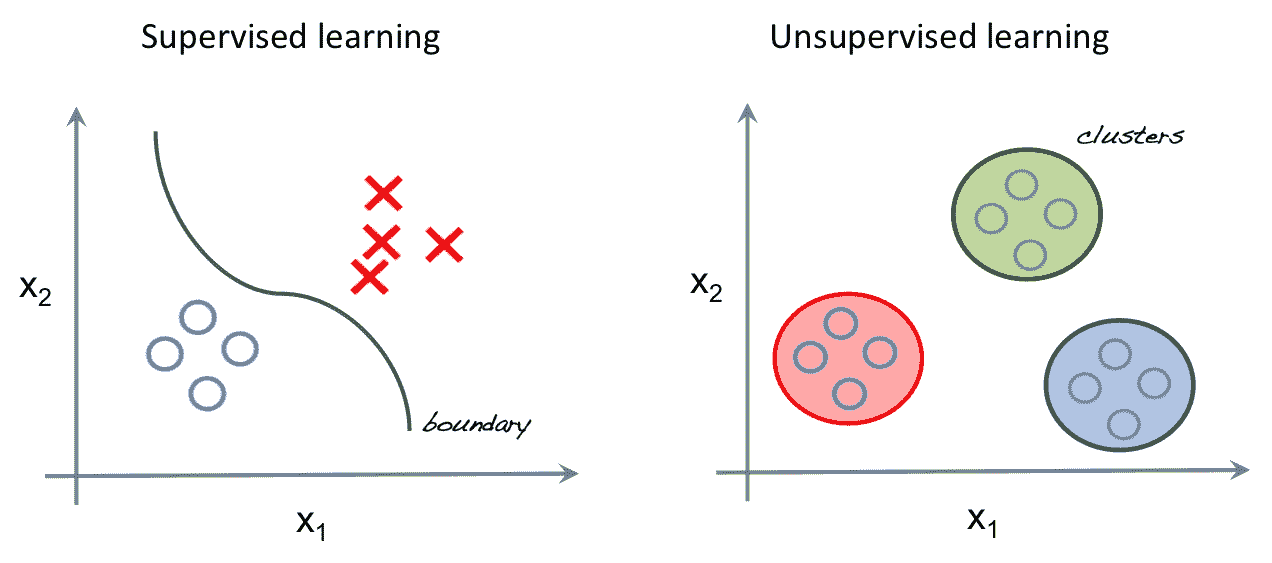
强化学习:第三种是关于训练智能体在环境中执行某些操作的全部。 我们知道理想的结果,但不知道如何实现。 我们没有给数据加标签,而是给智能体提供反馈,告诉它完成任务的好坏。 强化学习超出了本书的范围。
新旧机器学习
ML 工程师可能会遵循的典型流程来开发预测模型,如下所示:
- 收集数据
- 从数据中提取相关特征
- 选择 ML 架构(CNN,ANN,SVM,决策树等)
- 训练模型
- 评估模型并重复步骤 3 至 5,直到找到满意的解决方案
- 在现场测试模型
如前一节所述,机器学习的思想是拥有足够灵活的算法来学习数据背后的基础过程。 可以这么说,许多经典的 ML 方法不够强大,无法直接从数据中学习。 他们需要在使用这些算法之前以某种方式准备数据。
我们之前曾简要提到过,但是准备数据的过程通常称为特征提取,其中一些专家会过滤掉我们认为与其基础过程有关的所有数据细节。 此过程使所选分类器的分类问题更加容易,因为它不必处理数据中不相关的变量,否则这些变量可能会显得很重要。
ML 的新型深度学习方法具有的最酷的功能是,它们不需要(或需要更少)特征提取阶段。 相反,使用足够大的数据集,模型本身就能够直接从数据本身中学习代表数据的最佳特征! 这些新方法的示例如下:
- 深度 CNN
- 深度自编码器
- 生成对抗网络(GAN)
所有这些方法都是深度学习过程的一部分,在该过程中,大量数据暴露于多层神经网络。 但是,这些新方法的好处是有代价的。 所有这些新算法都需要更多的计算资源(CPU 和 GPU),并且比传统方法需要更长的训练时间。
人工神经网络
人工神经网络(ANN)受存在于我们大脑中的神经元生物网络的启发非常模糊,它由一组名为人工神经元的单元组成, 分为以下三种类型的层:
- 输入层
- 隐藏层
- 输出层
基本的人工神经元通过计算输入及其内部权重之间的点积来工作(参见下图),然后将结果传递给非线性激活函数f(在此示例中是 Sigmoid)。 然后将这些人工神经元连接在一起以形成网络。 在训练该网络期间,目标是找到合适的权重集,这些权重将有助于我们希望网络执行的任何任务:
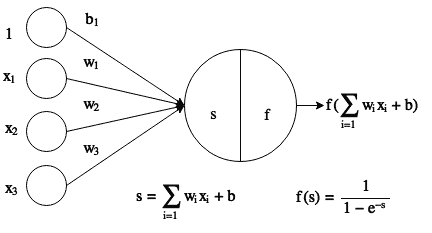
接下来,我们有一个 2 层前馈人工神经网络的示例。 想象一下,神经元之间的联系就是训练过程中将学习的权重。 在此示例中,层L1将是输入层,L2隐藏层,而L3将是输出层。 按照惯例,在计算层数时,我们仅包括权重可学习的层; 因此,我们不包括输入层。 这就是为什么它只是一个 2 层网络:
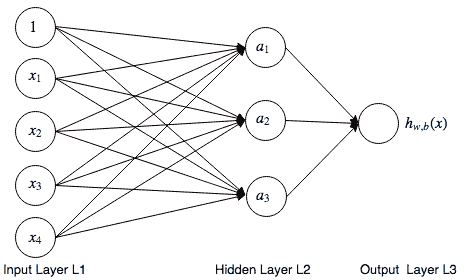
一层以上的神经网络是非线性假设的示例,在该模型中,模型可以学习比线性分类器更复杂的关系。 实际上,它们实际上是通用逼近器,能够逼近任何连续函数。
激活函数
为了使 ANN 模型能够解决更复杂的问题,我们需要在神经元点积之后添加一个非线性块。 然后,如果将这些非线性层级联起来,它将使网络将不同的概念组合在一起,从而使复杂的问题更易于解决。
在神经元中使用非线性激活非常重要。 如果我们不使用非线性激活函数,那么无论我们层叠了多少层,我们都只会拥有行为类似于线性模型的东西。 这是因为线性函数的任何线性组合都会分解为线性函数。
我们的神经元可以使用多种不同的激活函数,此处显示了一些; 唯一重要的是函数是非线性的。 每个激活函数都有其自身的优点和缺点。
历史上,神经网络选择的激活函数是 Sigmoid 和 TanH。 但是,这些功能对于可靠地训练神经网络不利,因为它们具有不希望的特性,即它们的值在任一端都饱和。 这将导致这些点处的梯度为零,我们将在后面找到,并且在训练神经网络时不是一件好事。

结果,更流行的激活函数之一是 ReLU 激活或整流线性单元。 ReLU 只是max(x, 0),输入和 0 之间的最大运算。 它具有理想的特性,即梯度(至少在一端)不会变为零,这极大地有助于神经网络训练的收敛速度。
该激活函数用于帮助训练深层的 CNN 之后,变得越来越流行。 它的简单性和有效性使其成为通常使用的激活函数。
XOR 问题
为了解释深度在 ANN 中的重要性,我们将研究一个 ANN 能够解决的非常简单的问题,因为它具有多个层。
在使用人工神经元的早期,人们并不像我们在人工神经网络中那样将各层级联在一起,因此我们最终得到了一个称为感知器的单层:
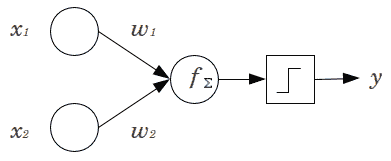
感知器实际上只是输入和一组学习的权重之间的点积,这意味着它实际上只是线性分类器。
大约在第一个 AI 冬季,人们意识到了感知器的弱点。 由于它只是线性分类器,因此无法解决简单的非线性分类问题,例如布尔异或(XOR)问题。 为了解决这个问题,我们需要更深入地研究。
在此图中,我们看到了一些不同的布尔逻辑问题。 线性分类器可以解决 AND 和 OR 问题,但不能解决 XOR:
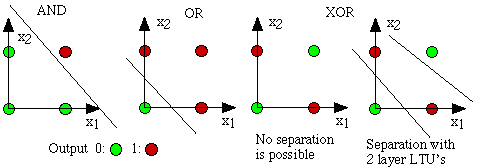
这使人们有了将使用非线性激活的神经元层级联在一起的想法。 一层可以根据上一层的输出来创建非线性概念。 这种“概念的组合”使网络变得更强大,并能代表更困难的功能,因此,它们能够解决非线性分类问题。
训练神经网络
那么,我们该如何在神经网络中设置权重和偏差的值,从而最好地解决我们的问题呢? 好吧,这是在训练阶段完成的。 在此阶段中,我们希望使神经网络从训练数据集中“学习”。 训练数据集由一组输入(通常表示为 X)以及相应的所需输出或标签(通常表示为 Y)组成。
当我们说网络学习时,所发生的就是网络参数被更新,网络应该能够为训练数据集中的每个 X 输出正确的 Y。 期望的是,在对网络进行训练之后,它将能够针对训练期间未看到的新输入进行概括并表现良好。 但是,为了做到这一点,您必须有一个足够具有代表性的数据集,以捕获要输出的内容。 例如,如果要分类汽车,则需要具有不同类型,颜色,照度等的数据集。
通常,当我们没有足够的数据或者我们的模型不够复杂以至于无法捕获数据的复杂性时,就会出现训练机器学习模型的一个常见错误。 这些错误可能导致过拟合和欠拟合的问题。 在以后的章节中,您将学习如何在实践中处理这些问题。
在训练期间,以两种不同的模式执行网络:
- 正向传播:我们通过网络向前工作,为数据集中的当前给定输入生成输出结果。 然后评估损失函数,该函数告诉我们网络在预测正确输出方面的表现如何。
- 反向传播:我们通过网络进行反向计算,计算每个权重对产生网络电流损失的影响。
此图显示了训练时网络运行的两种不同方式。

当前,使神经网络“学习”的主力军是与基于梯度的优化器(例如梯度下降)结合的反向传播算法。
反向传播用于计算梯度,该梯度告诉我们每个权重对产生电流损失有什么影响。 找到梯度后,可以使用诸如梯度下降之类的优化技术来更新权重,以使损失函数的值最小化。
谨在最后一句话:TensorFlow,PyTorch,Caffe 或 CNTK 之类的 ML 库将提供反向传播,优化器以及表示和训练神经网络所需的所有其他功能,而无需您自己重写所有这些代码。
反向传播和链式规则
反向传播算法实际上只是微积分中可信赖链规则的一个示例。 它说明了如何找到某个输入对由多个功能组成的系统的影响。 因此,例如在下图中,如果您想知道x对函数g的影响,我们只需将f对g的影响乘以x对f的影响:
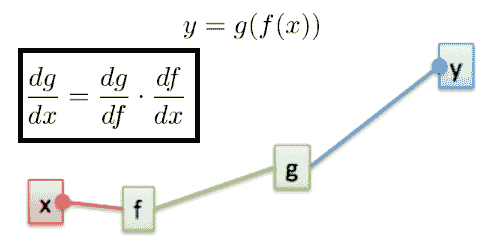
同样,这意味着如果我们想实现自己的深度学习库,则需要定义层的正常计算(正向传播)以及此计算块相对于其输入的影响(导数)。
下面我们给出一些常见的神经网络操作及其梯度。
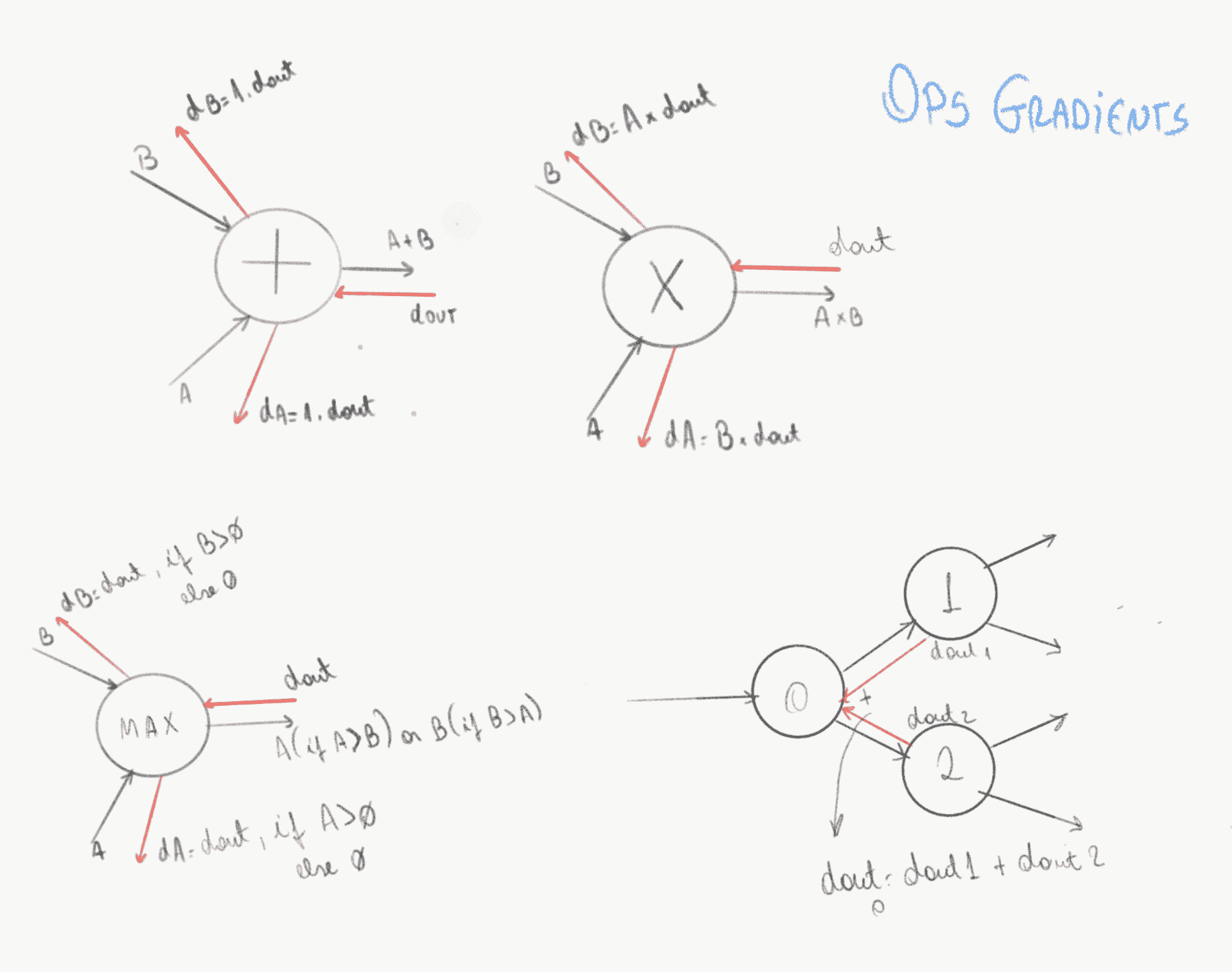
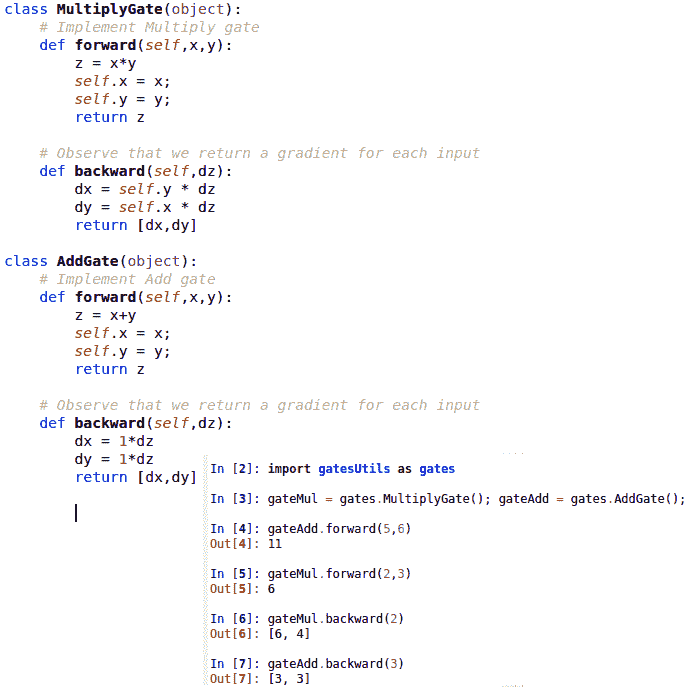
批量
对于大型数据集而言,将整个数据集存储在内存中以训练网络的想法,例如第 1 章,“TensorFlow 简介和设置”中的示例。 人们在实践中所做的是,在训练期间,他们将数据集分成小块,称为迷你批次(通常称为批次)。 然后,依次将每个微型批次装入并馈送到网络,在网络中将计算反向传播和梯度下降算法,然后更新权重。 然后,对每个小批量重复此操作,直到您完全浏览了数据集。
为小批量计算的梯度是对整个训练集的真实梯度的噪声估计,但是通过反复获取这些小的噪声更新,我们最终仍将收敛到足够接近损失函数的最小值。
较大的批次大小可以更好地估计真实梯度。 使用较大的批次大小将允许较大的学习率。 权衡是在训练时需要更多的内存来保存此批次。
当模型看到您的整个数据集时,我们说一个周期已经完成。 由于训练的随机性,您将需要针对多个周期训练模型,因为您的模型不可能只在一个周期内收敛。
损失函数
在训练阶段,我们需要使用当前的权重正确预测训练集; 此过程包括评估我们的训练集输入 X ,并与所需的输出 Y 进行比较。 需要某种机制来量化(返回标量数)我们当前的权重在正确预测我们所需的输出方面有多好。 该机制称为损失函数。
反向传播算法应返回每个参数相对于损失函数的导数。 这意味着我们将发现更改每个参数将如何影响损失函数的值。 然后,优化算法的工作就是最小化损失函数,换句话说,就是在训练时减小训练误差。
一个重要方面是为工作选择合适的损失函数。 一些最常见的损失函数及其用途是在此处给出的:
- 对数损失 - 仅具有两个可能结果的分类任务(从有限集中返回标签)
- 交叉熵损失 - 具有两个以上结果的分类任务(从有限集返回标签)
- L1 损失 - 回归任务(返回实数值)
- L2 损失 - 回归任务(返回实数值)
- Huber 损失 - 回归任务(返回实数值)
在本书中,我们将看到损失函数的不同示例。
损失函数的另一个重要方面是它们必须是可微分的。 否则,我们不能将它们与反向传播一起使用。 这是因为反向传播要求我们能够采用损失函数的导数。
在下图中,您可以看到损失函数连接在神经网络的末端(模型输出),并且基本上取决于模型的输出和数据集所需的目标。

TensorFlow 的以下代码行也显示了这一点,因为损失仅需要标签和输出(此处称为对率)。
loss = tf.losses.sparse_softmax_cross_entropy(labels=labels, logits=logits)
您可能会注意到第三个箭头也连接到损失函数。 这与名为正则化的东西有关,将在第 3 章“TensorFlow 中的图像分类”中进行探讨; 因此,现在您可以放心地忽略它。
优化器及其超参数
如前所述,优化器的工作是以一种使训练损失误差最小的方式来更新网络权重。 在所有 TensorFlow 之类的深度学习库中,实际上只使用了一个优化器系列,即梯度下降式优化器系列。
其中最基本的简称为梯度下降(有时称为香草梯度下降),但已经尝试开发出更复杂的梯度下降方法。 一些受欢迎的是:
- 带动量的梯度下降
- RMSProp
- Adam
TensorFlow 的所有不同优化器都可以在tf.train类中找到。 例如,可以通过调用tf.train.AdamOptimizer()使用 Adam 优化器。
您可能会怀疑,它们都有可配置的参数来控制它们的工作方式,但是通常最需要注意和更改的参数如下:
- 学习率:控制优化器尝试最小化损失函数的速度。 将其设置得太高,您将无法收敛到最小。 将其设置得太小,将永远收敛或陷于不良的局部最小值中。
下图显示了学习率选择错误可能带来的问题:

学习率的另一个重要方面是,随着训练的进行和误差的减少,您在训练开始时选择的学习率值可能会变得太大,因此您可能会开始超出最小值。
要解决此问题,您可以安排学习率衰减,以免在训练时降低学习率。 这个过程称为学习率调度,我们将在下一章中详细讨论几种流行的方法。
另一种解决方案是使用自适应优化器之一,例如 Adam 或 RMSProp。 这些优化器经过精心设计,可在您训练时自动调整和衰减所有模型参数的学习率。 这意味着从理论上讲,您不必担心安排自己的学习率下降。
最终,您希望选择优化器,以最快,最准确的方式训练您的网络。 下图显示了优化器的选择如何影响网络收敛的速度。 不同的优化器之间可能会有相当大的差距,并且可能因不同的问题而有所不同,因此理想情况下,如果可以的话,您应该尝试所有的优化器,并找到最适合您的问题的解决方案。
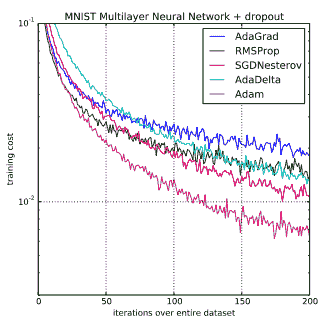
但是,如果您没有时间执行此操作,那么下一个最佳方法是首先尝试将 Adam 用作优化器,因为它通常在很少调整的情况下效果很好。 然后,如果有时间,请尝试使用 Momentum SGD; 这将需要更多的参数调整,例如学习率,但是如果调整得很好,通常会产生非常好的结果。
欠拟合与过拟合
在设计用于解决特定问题的神经网络时,我们可能有很多活动部件,并且必须同时处理许多事情,例如:
- 准备数据集
- 选择层数/神经元数
- 选择优化器超参数
如果我们专注于第二点,它使我们了解选择或设计神经网络架构/结构时可能发生的两个问题。
这些问题中的第一个是模型对于训练数据的数量或复杂性而言是否太大。 由于模型具有如此众多的参数,因此即使在数据中存在噪声的情况下,它也可以轻松轻松地准确地学习其在训练集中看到的内容。 这是一个问题,因为当向网络提供的数据与训练集不完全相同时,网络将无法正常运行,因为它过于精确地了解了数据的外观,而错过了其背后的全局。 这个问题称为过拟合或具有高方差。
另一方面,您可能选择的网络规模不足以捕获数据复杂性。 现在,我们遇到了相反的问题,由于您的模型没有足够的能力(参数)来充分学习,因此您的模型无法充分捕获数据集背后的基础结构。 网络将再次无法对新数据执行良好的操作。 这个问题称为欠拟合或具有高偏差。
您可能会怀疑,在模型复杂性方面,您总是会寻求适当的平衡,以避免这些问题。
在后面的章节中,我们将看到如何检测,避免和补救这些问题,但是仅出于介绍的目的,这些是解决这些问题的一些经典方法:
- 获取更多数据
- 当检测到测试数据的误差开始增长时停止(提前停止)
- 尽可能简单地开始模型设计,并且仅在检测到欠拟合时才增加复杂性
特征缩放
为了简化优化程序算法的工作,在训练和测试之前,有一些技术可以并且应该应用到您的数据中。
如果输入向量的不同维度上的值彼此不成比例,则损失空间将以某种方式扩大。 这将使梯度下降算法难以收敛,或者至少使其收敛较慢。
当数据集的特征超出比例时,通常会发生这种情况。 例如,关于房屋的数据集在输入向量中的一个特征可能具有“房间数”,其值可能在 1 到 4 之间,而另一个特征可能是“房屋面积”,并且可能在 1000 到 10000 之间。 ,它们彼此之间严重超出比例,这可能会使学习变得困难。
在下面的图片中,我们看到一个简单的示例,说明如果我们的输入特征未全部按比例缩放,则损失函数的外观以及正确缩放比例后的外观。 当数据缩放不正确时,梯度下降很难达到损失函数的最小值。
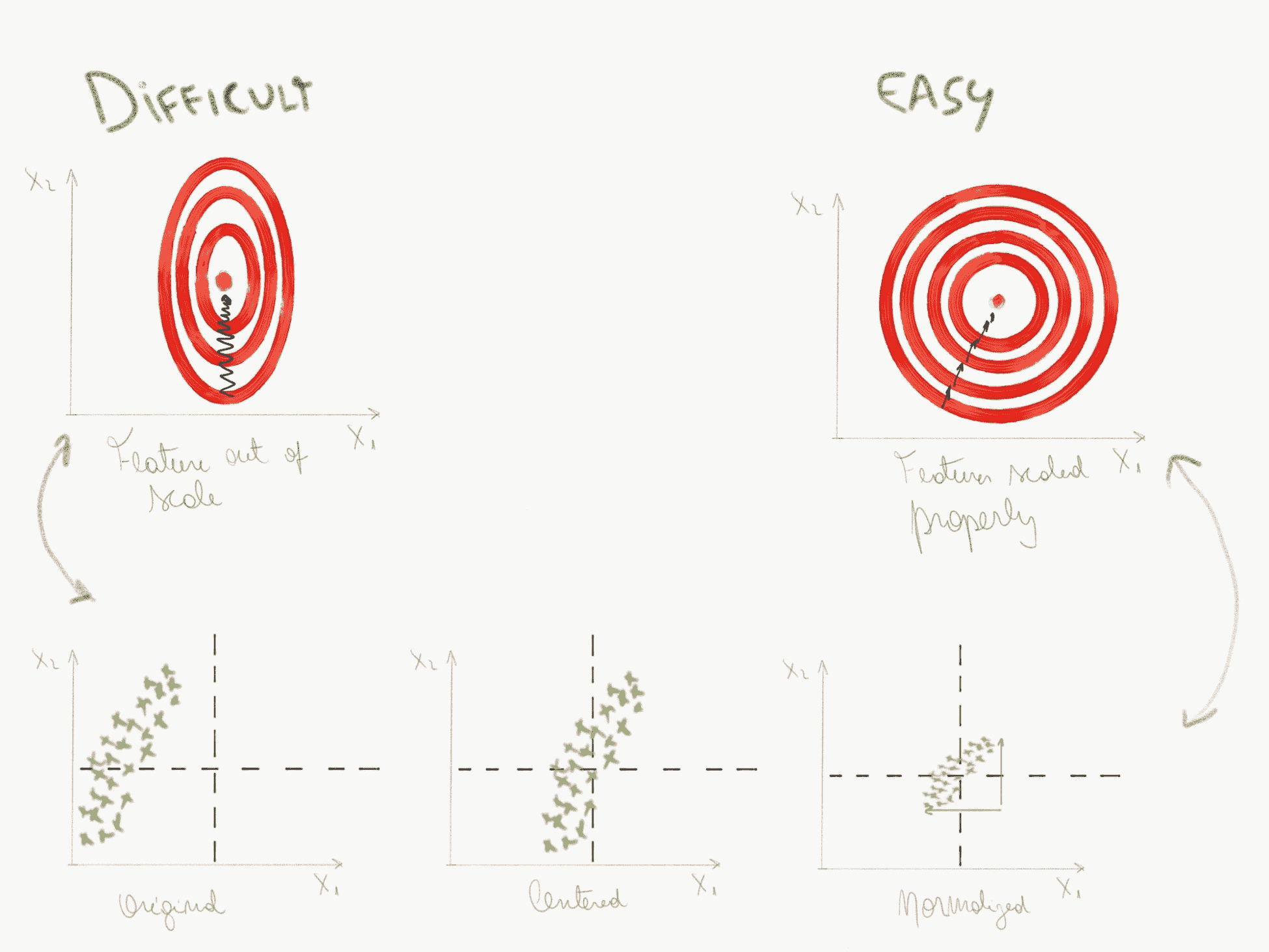
通常,您将对数据进行一些标准化,例如在使用数据之前减去平均值并除以数据集的标准差。 对于 RGB 图像,通常只需从每个像素值中减去 128 即可使数据居中于零附近。 但是,更好的方法是为数据集中的每个图像通道计算平均像素值。 现在,您具有三个值,每个图像通道一个,现在从输入图像中删除这些值。 我们一开始就不必担心缩放问题,因为所有功能一开始的缩放比例都相同(0-255)。
要记住非常重要的一点-如果您在训练时对数据进行了一些预处理,则必须在测试时进行完全相同的预处理,否则可能会得到不好的结果!
全连接层
组成我们之前看到的 ANN 的神经元层通常称为密集连接层,或全连接(FC)层,或简称为线性层。 诸如 Caffe 之类的一些深度学习库实际上会将它们视为点乘积运算,非线性层可能会或可能不会跟随它们。 它的主要参数将是输出大小,基本上是其输出中神经元的数量。
在第 1 章,“TensorFlow 简介和设置”中,我们创建了自己的致密层,但是您可以使用tf.layers来更轻松地创建它,如下所示:
dense_layer = tf.layers.dense(inputs=some_input_layer, units=1024, activation=tf.nn.relu)
在这里,我们定义了一个具有 1,024 个输出的完全连接层,随后将激活 ReLU。
重要的是要注意,该层的输入必须仅具有二维,因此,如果您的输入是空间张量,例如形状为[28 * 28 * 3]的图像,则必须在输入之前将其重整为向量:
reshaped_input_to_dense_layer = tf.reshape(spatial_tensor_in, [-1, 28 * 28 * 3])
针对 XOR 问题的 TensorFlow 示例
在这里,我们将到目前为止已经了解的一些知识放在一起,并将使用 TensorFlow 解决布尔 XOR 问题。 在此示例中,我们将创建一个具有 Sigmoid 激活函数的三层神经网络。 我们使用对数损失,因为网络 0 或 1 仅有两种可能的结果:
import tensorflow as tf
# XOR dataset
XOR_X = [[0, 0], [0, 1], [1, 0], [1, 1]]
XOR_Y = [[0], [1], [1], [0]]
num_input = 2
num_classes = 1
# Define model I/O (Placeholders are used to send/get information from graph)
x_ = tf.placeholder("float", shape=[None, num_input], name='X')
y_ = tf.placeholder("float", shape=[None, num_classes], name='Y')
# Model structure
H1 = tf.layers.dense(inputs=x_, units=4, activation=tf.nn.sigmoid)
H2 = tf.layers.dense(inputs=H1, units=8, activation=tf.nn.sigmoid)
H_OUT = tf.layers.dense(inputs=H2, units=num_classes, activation=tf.nn.sigmoid)
# Define cost function
with tf.name_scope("cost") as scope:
cost = tf.losses.log_loss( labels=y_, predictions=H_OUT)
# Add loss to tensorboard
tf.summary.scalar("log_loss", cost)
# Define training ops
with tf.name_scope("train") as scope:
train_step = tf.train.GradientDescentOptimizer(0.1).minimize(cost)
merged_summary_op = tf.summary.merge_all()
# Initialize variables(weights) and session
init = tf.global_variables_initializer()
sess = tf.Session()
# Configure summary to output at given directory
writer = tf.summary.FileWriter("./logs/xor_logs", sess.graph)
sess.run(init)
# Train loop
for step in range(10000):
# Run train_step and merge_summary_op
_, summary = sess.run([train_step, merged_summary_op], feed_dict={x_: XOR_X, y_: XOR_Y})
if step % 1000 == 0:
print("Step/Epoch: {}, Loss: {}".format(step, sess.run(cost, feed_dict={x_: XOR_X, y_: XOR_Y})))
# Write to tensorboard summary
writer.add_summary(summary, step)
如果运行此脚本,则应该期望获得以下损失图。 我们可以看到损失已经为零,这表明模型已经过训练并解决了问题。 您可以重复此实验,但现在只有一层致密层; 正如我们所说,您应该注意到该模型无法解决问题
 。
。
为了能够查看图,可以在脚本提示符下的命令提示符下运行以下命令。 这将为我们启动 tensorboard。 我们将在本章的后面找到关于 tensorboard 的更多信息。
$ tensorboard --logdir=./logs/xor_logs
卷积神经网络
现在,我们将讨论另一种类型的神经网络,该网络专门设计用于处理具有某些空间特性的数据,例如图像。 这种类型的神经网络称为卷积神经网络(CNN)。
CNN 主要由称为卷积层的层组成,这些层对其层输入进行过滤以在这些输入中找到有用的特征。 这种过滤操作称为卷积,从而产生了这种神经网络的名称。
下图显示了对图像的二维卷积运算及其结果。 重要的是要记住,过滤器内核的深度与输入的深度相匹配(在这种情况下为 3):

同样重要的是要清楚卷积层的输入不必是 1 或 3 通道图像。 卷积层的输入张量可以具有任意数量的通道。
很多时候,在谈论 CNN 中的卷积层时,人们都喜欢将卷积这个词简称为conv。 这是非常普遍的做法,我们在本书中也会做同样的事情。
卷积
卷积运算是由星号表示的线性运算,它将两个信号合并:

二维卷积在图像处理中用于实现图像过滤器,例如,查找图像上的特定补丁或查找图像中的某些特征。
在 CNN 中,卷积层使用称为内核的小窗口,以类似于瓦片的方式过滤输入张量。 内核精确定义了卷积运算将要过滤的内容,并且在找到所需内容时会产生强烈的响应。
下图显示了将图像与称为 Sobel 过滤器的特定内核进行卷积的结果,该内核非常适合在图像中查找边:
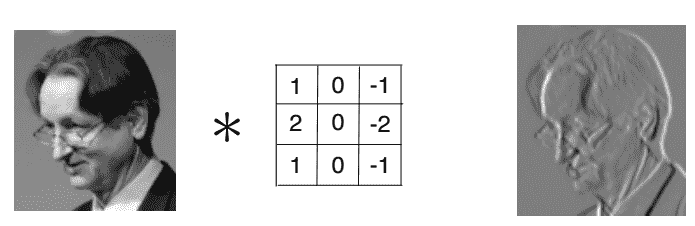
您可能已经猜到了,在卷积层中要学习的参数是该层内核的权重。 在 CNN 训练期间,这些过滤器的值会自动调整,以便为手头任务提取最有用的信息。
在传统的神经网络中,我们将必须将任何输入数据转换为单个一维向量,从而在将该向量发送到全连接层后丢失所有重要的空间信息。 此外,每个像素每个神经元都有一个参数,导致输入大小或输入深度较大的模型中参数数量激增。
但是,在卷积层的情况下,每个内核将在整个输入中“滑动”以搜索特定补丁。 CNN 中的内核很小,并且与它们所卷积的大小无关。 结果,就参数而言,使用卷积层的开销通常比我们之前了解的传统密集层要少得多。
下图显示了传统的完全连接层和卷积(局部连接)层之间的区别。 注意参数的巨大差异:

现在,也许我们希望卷积层在其输入中查找六种不同的事物,而不仅仅是寻找一种。 在这种情况下,我们将只给卷积层六个相同大小的过滤器(在这种情况下为5x5x3),而不是一个。 然后,每个转换过滤器都会在输入中查找特定的模式。
下图显示了此特定的六个过滤器卷积层的输入和输出:

控制卷积层行为的主要超参数如下:
- 内核大小(K):滑动窗口的像素大小。 小通常更好,通常使用奇数,例如 1、3、5,有时很少使用 7。
- 跨度(S):内核窗口在卷积的每个步骤中将滑动多少像素。 通常将其设置为 1,因此图像中不会丢失任何位置,但是如果我们想同时减小输入大小,则可以增加位置。
- 零填充(P):要放在图像边框上的零数量。 使用填充使内核可以完全过滤输入图像的每个位置,包括边。
- 过滤器数(F):我们的卷积层将具有多少个过滤器。 它控制卷积层将要查找的图案或特征的数量。
在 TensorFlow 中,我们将在tf.layers模块中找到 2D 卷积层,可以将其添加到模型中,如下所示:
conv1 = tf.layers.conv2d(
inputs=input_layer,
filters=32,
kernel_size=[5, 5],
padding="same",
activation=tf.nn.relu)
输入填充
如果我们什么都不做,那么卷积运算将输出一个在空间上小于输入结果的结果。 为了避免这种影响并确保卷积核查看每个图像位置,我们可以在输入图像的边界上放置零。 当我们这样做时,据说我们要填充图像:
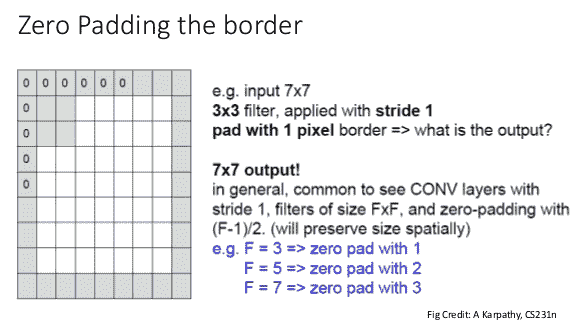
TensorFlow 卷积操作为您提供了两种用于填充需求的选项:相同和有效。
- 有效-TensorFlow 不填充图像。 卷积内核将仅进入输入中的“有效”位置。
- 相同-如果我们假设步幅为 1,则在这种情况下,TensorFlow 将足够填充输入,以便输出空间大小与输入空间大小相同。
如果您确实希望对填充有更多控制,则可以在层的输入上使用tf.pad(),以用所需的零个位数来填充输入。
通常,我们可以使用以下公式计算卷积运算的输出大小:
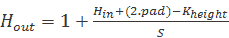
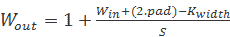
(这里,pad是添加到每个边框的零的数量。)
但是在 TensorFlow 中,由于有效和相同填充选项的性质,公式如下所示:
# Same padding
out_height = ceil(float(in_height) / float(strides[1]))
out_width = ceil(float(in_width) / float(strides[2]))
# Valid padding
out_height = ceil(float(in_height - filter_height + 1) / float(strides[1]))
out_width = ceil(float(in_width - filter_width + 1) / float(strides[2]))
计算参数数量(权重)
在这里,我们将展示如何计算卷积层使用的参数数量。 计算卷积层中参数数量(包括偏差)的公式如下:
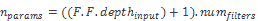
我们将用一个简单的例子来说明:
Input: [32x32x3] input tensor
Conv layer: Kernel:5x5
numFilters:10
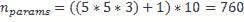
另一方面,全连接层中的参数数量(包括偏置)如下:

如前所述,如果直接在图像上使用传统的人工神经网络,则所有空间信息都将丢失,并且每个参数每个神经元每个像素只有一个参数,因此会有大量的参数。 使用前面提到的相同示例,并在密集的 10 个输出神经元层中,我们得到以下数字:
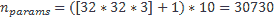
这证明了这两种层类型之间参数的数量级差异。
计算操作数量
现在,我们对计算特定卷积层的计算成本感兴趣。 如果您想了解如何实现有效的网络结构(例如在移动设备中速度是关键时),则此步骤很重要。 另一个原因是要查看在硬件中实现特定层需要多少个乘法器。 现代 CNN 架构中的卷积层最多可负责模型中所有计算的 90%!
这些是影响 MAC(乘加累加器)/操作数量的因素:
- 卷积核大小(
F) - 过滤器数量(
M) - 输入特征图的高度和宽度(
H,W) - 输入批量(
B) - 输入深度大小(通道)(
C) - 卷积层步幅(
S)
MAC 的数量可以计算为:
#MAC = [F * F * C * (H + 2 * P-FS + 1) * (W + 2 * P-FS + 1) * M] * B
例如,让我们考虑一个具有输入224 x 224 x 3,批量大小为 1,内核为3x3、64 个过滤器,跨度为 1 和填充 1 的转换层:
#MAC = 3 * 3 * (224 + 2-31 + 1) * (224 + 2-31 + 1) * 3 * 64 * 1 = 9,462,528
相反,全连接层具有以下操作数:
#MAC = [H * W * C * Outputneurons] * B
让我们重用相同的示例,但现在有 64 个神经元的密集层:
#MAC = [224 * 224 * 3 * 64] * 1 = 9,633,792
(我们已排除了所有运维计算的偏差,但不应增加太多成本。)
通常,在 CNN 中,早期的卷积层贡献了大部分计算成本,但参数最少。 在网络的末尾,相反的情况是后面的层具有更多的参数,但计算成本却较低。
将卷积层转换为全连接层
实际上,我们可以将全连接层视为卷积层的子集。 如果我们将内核大小设置为与输入大小匹配,则可以将 CNN 层转换为全连接层。 设置过滤器的数量与设置完全连接层中输出神经元的数量相同。 检查一下自己,在这种情况下,操作将是相同的。
例:
考虑具有 4,096 个输出神经元和输入大小为7x7x512的 FC 层,转换为:
转换层:内核:7x7,填充:0:步幅:1,过滤器:4,096。
使用公式来计算输出大小,我们得到大小为1 x 1 x 4096的输出。
这样做的主要原因之一是使您的网络完全卷积。 当网络完全卷积时,决定使用比输入的图像更大的输入大小图像并不重要,因为您没有任何需要固定输入大小的全连接层。
池化层
池化层用于减少 CNN 中我们的激活张量的空间尺寸,而不是体积深度。 它们是执行此操作的非参数方式,这意味着池化层中没有权重。 基本上,以下是从使用池中获得的收益:
- 在输入张量中汇总空间相关信息的简单方法
- 通过减少空间信息,您可以获得计算性能
- 您的网络中存在一些平移不变性
但是,池化的最大优点之一是它无需学习任何参数,这也是它的最大缺点,因为池化最终可能会丢掉重要的信息。 结果,现在开始在 CNN 中使用池的频率降低了。
在此图中,我们显示了最大池化池的最常见类型。 它像普通的卷积一样滑动一个窗口,然后在每个位置将窗口中的最大值设置为输出:
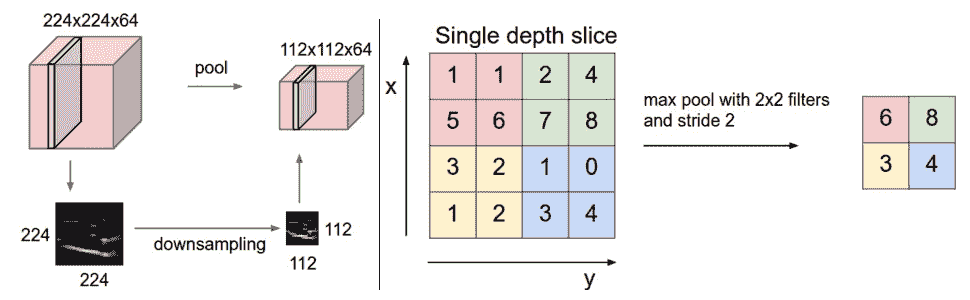
在 TensorFlow 中,我们可以这样定义池层:
tf.layers.max_pooling2d(inputs=some_input_layer, pool_size=[2, 2], strides=2)
1x1卷积
这种卷积起初看起来可能有些奇怪,但是1x1卷积实际上是通过合并深度来适应深度的,而不更改空间信息。 当需要在不损失空间信息的情况下将一个体积深度转换为另一个体积深度(称为压缩或扩展)时,可以使用这种类型的卷积:

计算感受域
感受域是特定卷积窗口“看到”其输入张量的程度。
有时,确切了解激活中每个特定像素在输入图像中“看到”了多少像素可能很有用; 这在对象检测系统中尤其重要,因为我们需要以某种方式查看某些层激活如何映射回原始图像大小。
在下图中,我们可以看到三个连续的3x3卷积层的感受域与一个7x7卷积层的感受域相同。 在设计新的更好的 CNN 模型时,此属性非常重要,我们将在后面的章节中看到。

感受域可以计算为:

在这里,组件如下:
R[k]:k层的感受域Kernel[k]:第k层的内核大小S[i]:第i层(1..k-1)的跨步∏s[i], i=1..(k-1):直到第k-1层的所有步长的乘积(所有先前的层,而不是当前的一层)
仅对于第一层,接收域就是内核大小。
这些计算与是否使用卷积或池化层无关,例如,步幅为 2 的卷积层将与步幅为 2 的池化层具有相同的感受域。
例如,给定以下层之后的14x14x3图像,这将适用:
- 卷积:S:1,P:0,K:3
- 卷积:S:1,P:0,K:3
- 最大池化:S:2,P:0,K2
- 卷积:S:1,P:0,K:3

在 TensorFlow 中构建 CNN 模型
在开始之前,有个好消息:使用 TensorFlow,您无需担心编写反向传播或梯度下降代码,而且所有常见类型的层都已实现,因此事情应该更轻松。
在此处的 TensorFlow 示例中,我们将根据您在第 1 章,“TensorFlow 简介和设置”中学到的内容进行一些更改,并轻松自如地使用tf.layers API 创建我们的整个网络:
import tensorflow as tf
from tensorflow.examples.tutorials.mnist import input_data
mnist = input_data.read_data_sets("MNIST_data/", one_hot=True)
# MNIST data input (img shape: 28*28)
num_input = 28*28*1
# MNIST total classes (0-9 digits)
num_classes = 10
# Define model I/O (Placeholders are used to send/get information from graph)
x_ = tf.placeholder("float", shape=[None, num_input], name='X')
y_ = tf.placeholder("float", shape=[None, num_classes], name='Y')
# Add dropout to the fully connected layer
is_training = tf.placeholder(tf.bool)
# Convert the feature vector to a (-1)x28x28x1 image
# The -1 has the same effect as the "None" value, and will
# be used to inform a variable batch size
x_image = tf.reshape(x_, [-1, 28, 28, 1])
# Convolutional Layer #1
# Computes 32 features using a 5x5 filter with ReLU activation.
# Padding is added to preserve width and height.
# Input Tensor Shape: [batch_size, 28, 28, 1]
# Output Tensor Shape: [batch_size, 28, 28, 32]
conv1 = tf.layers.conv2d(inputs=x_image, filters=32, kernel_size=[5, 5], padding="same", activation=tf.nn.relu)
# Pooling Layer #1
# First max pooling layer with a 2x2 filter and stride of 2
# Input Tensor Shape: [batch_size, 28, 28, 32]
# Output Tensor Shape: [batch_size, 14, 14, 32]
pool1 = tf.layers.max_pooling2d(inputs=conv1, pool_size=[2, 2], strides=2)
# Convolutional Layer #2
# Computes 64 features using a 5x5 filter.
# Input Tensor Shape: [batch_size, 14, 14, 32]
# Output Tensor Shape: [batch_size, 14, 14, 64]
conv2 = tf.layers.conv2d( inputs=pool1, filters=64, kernel_size=[5, 5], padding="same", activation=tf.nn.relu)
# Pooling Layer #2
# Second max pooling layer with a 2x2 filter and stride of 2
# Input Tensor Shape: [batch_size, 14, 14, 64]
# Output Tensor Shape: [batch_size, 7, 7, 64]
pool2 = tf.layers.max_pooling2d(inputs=conv2, pool_size=[2, 2], strides=2)
# Flatten tensor into a batch of vectors
# Input Tensor Shape: [batch_size, 7, 7, 64]
# Output Tensor Shape: [batch_size, 7 * 7 * 64]
pool2_flat = tf.reshape(pool2, [-1, 7 * 7 * 64])
# Dense Layer
# Densely connected layer with 1024 neurons
# Input Tensor Shape: [batch_size, 7 * 7 * 64]
# Output Tensor Shape: [batch_size, 1024]
dense = tf.layers.dense(inputs=pool2_flat, units=1024, activation=tf.nn.relu)
# Add dropout operation; 0.6 probability that element will be kept
dropout = tf.layers.dropout( inputs=dense, rate=0.4, training=is_training)
# Logits layer
# Input Tensor Shape: [batch_size, 1024]
# Output Tensor Shape: [batch_size, 10]
logits = tf.layers.dense(inputs=dropout, units=10)
# Define a loss function (Multinomial cross-entropy) and how to optimize it
cross_entropy = tf.reduce_mean(tf.nn.softmax_cross_entropy_with_logits(logits=logits, labels=y_))
train_step = tf.train.AdamOptimizer(1e-4).minimize(cross_entropy)
correct_prediction = tf.equal(tf.argmax(logits,1), tf.argmax(y_,1))
accuracy = tf.reduce_mean(tf.cast(correct_prediction, tf.float32))
# Build graph
init = tf.global_variables_initializer()
# Avoid allocating the whole memory
gpu_options = tf.GPUOptions(per_process_gpu_memory_fraction=0.333)
sess = tf.Session(config=tf.ConfigProto(gpu_options=gpu_options))
sess.run(init)
# Train graph
for i in range(2000):
# Get batch of 50 images
batch = mnist.train.next_batch(50)
# Print each 100 epochs
if i % 100 == 0:
# Calculate train accuracy
train_accuracy = accuracy.eval(session=sess, feed_dict={x_: batch[0], y_: batch[1], is_training: True})
print("step %d, training accuracy %g" % (i, train_accuracy))
# Train actually here
train_step.run(session=sess, feed_dict={x_: batch[0], y_: batch[1], is_training: False})
print("Test Accuracy:",sess.run(accuracy, feed_dict={x_: mnist.test.images, y_: mnist.test.labels, is_training: False}))
TensorBoard
TensorBoard 是 TensorFlow 随附的基于 Web 的工具,可让您可视化构造的 TensorFlow 图。 最重要的是,它使您能够跟踪大量的统计数据或变量,这些数据或变量可能对训练模型很重要。 您可能希望跟踪的此类变量的示例包括训练损失,测试集准确率或学习率。 前面我们看到,我们可以使用张量板可视化损失函数的值。
要运行 TensorBoard,请打开一个新终端并输入以下内容:
$ tensorboard --logdir=/somepath
在这里,somepath指向您的训练代码保存张量板日志记录数据的位置。
在代码内部,您需要通过为每个张量创建一个tf.summary来定义要可视化的张量。 因此,例如,如果我们要检查所有可训练变量和损失,则需要使用以下代码:
with tf.Session() as sess:
"""Create your model"""
# Add all trainable variables to tensorboard
for var in tf.trainable_variables():
tf.summary.histogram(var.name, var)
# Add loss to tensorboard
tf.summary.scalar("softmax_cross_entropy", loss)
# Merge all summaries
merged_summary = tf.summary.merge_all()
# Initialize a summary writer
train_writer = tf.summary.FileWriter( /tmp/summarys/ , sess.graph)
train_writer.add_summary(merged_summary, global_step)
"""Training loop"""
我们需要创建一个tf.summar.FileWriter,它负责创建一个目录,该目录将存储我们的摘要日志。 如果在创建FileWriter时传递图,则该图也将显示在 TensorBoard 中。 通过传入sess.graph,我们提供了会话正在使用的默认图。 在 TensorBoard 中显示图的结果可能看起来像这样:
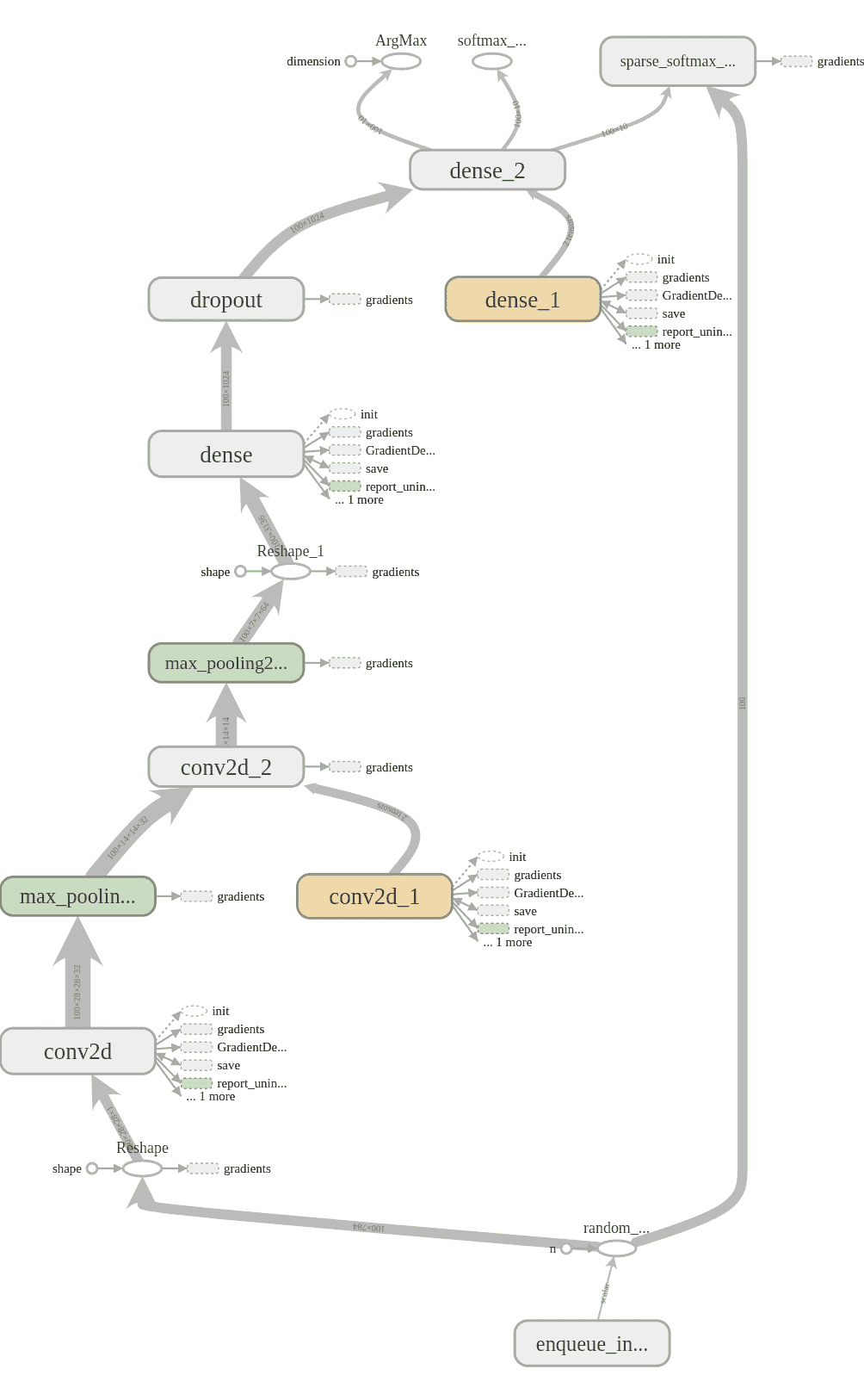
其他类型的卷积
本章的目的是让您了解 CNN 是什么,它们的用途以及如何在 TensorFlow 中构造它们。 但是,在这一点上值得一提的是,当今还有其他类型的卷积运算用于不同的目的,我们将在后面的章节中更详细地介绍其中的一些。
现在,我们将仅按名称和使用位置提及它们:
- 深度卷积:用于 MobileNets,旨在使卷积对移动平台友好
- 膨胀卷积(Atrous Convolution):它们具有称为膨胀率的额外参数,可让您以相同的计算成本获得更大的视野(例如
3x3卷积可以和5x5卷积具有相同的视野) - 转置卷积(Deconvolutions):通常用于 CNN 自编码器和语义分割问题
总结
在本章中,我们向您介绍了机器学习和人工智能。 我们研究了什么是人工神经网络以及如何对其进行训练。 在此之后,我们研究了 CNN 及其主要组成部分。 我们介绍了如何使用 TensorFlow 训练您自己的 CNN 以识别数字。 最后,我们对 Tensorboard 进行了介绍,并了解了如何在 TensorFlow 中训练模型时如何使用它来帮助可视化重要的统计数据。
在下一章中,我们将更仔细地研究图像分类的任务,以及如何使用 CNN 和 TensorFlow 来解决此任务。
三、TensorFlow 中的图像分类
图像分类是指根据图像内容将图像分类的问题。 让我们从分类的示例任务开始,其中图片可能是狗的图像,也可能不是。 某人可能要完成此任务的一种简单方法是,像在第 1 章中所做的那样,获取输入图像,将其重塑为向量,然后训练线性分类器(或其他某种分类器)。 但是,您很快就会发现此主意不好,原因有几个。 除了不能很好地缩放到输入图像的大小之外,线性分类器将很难将一个图像与另一个图像分开。
与可以在图像中看到有意义的图案和内容的人类相反,计算机只能看到从 0 到 255 的数字数组。对于同一类的不同图像,这些数字在相同位置的广泛波动导致无法直接将它们使用为分类器的输入。 从加拿大高级研究学院(CIFAR)数据集中获取的这 10 张示例狗图像完美地说明了此问题。 狗的外观不仅有所不同,而且它们在镜头前的姿势和位置也有所不同。 对于机器来说,每个图像一目了然,完全没有共同点,而我们人类却可以清楚地看到它们都是狗:









一个更好的解决方案是告诉计算机从输入图像中提取一些有意义的特征,例如常见的形状,纹理或颜色。 然后,我们可以使用这些功能而不是原始输入图像作为分类器的输入。 现在,我们正在寻找图像中这些功能的存在,以告诉我们图像是否包含我们要识别的对象。
这些提取的特征在我们看来将仅仅是一个高维向量(但通常比原始图像空间要小得多),可以用作分类器的输入。 多年来开发的一些著名的特征提取方法是尺度不变特征(SIFT),最大稳定的末端区域(MSER),本地二进制模式(LBP)和直方图定向梯度(HOG)。
当使用卷积神经网络进行图像分类时,2012 年是计算机视觉(以及随后的其他机器学习领域)最大的转折点之一,这标志着如何解决这一任务(以及许多其他问题)的方式发生了转变。 我们不是专注于手工制作更好的特征以从图像中提取,而是使用数据驱动的方法来找到代表问题数据集的最佳特征集。 CNN 将使用大量训练图像,并自己学习代表数据的最佳特征,以解决分类任务。
在本章中,我们将介绍以下主题:
- 看一下用于分类的损失函数
- Imagenet 和 CIFAR 数据集
- 训练 CNN 对 CIFAR 数据集进行分类
- 数据 API 简介
- 如何初始化权重
- 如何规范化模型来获得更好的结果
CNN 模型架构
图像分类模型的关键部分是其 CNN 层。 这些层将负责从图像数据中提取特征。 这些 CNN 层的输出将是一个特征向量,就像以前一样,我们可以将其用作所选分类器的输入。 对于许多 CNN 模型,分类器将只是连接到我们 CNN 输出的完全连接层。 如第 1 章,“TensorFlow 简介和设置”中所示,我们的线性分类器只是一个全连接层; 除了层的大小和输入会有所不同之外,这里就是这种情况。
重要的是要注意,分类或回归问题(例如定位)(或其他使用图像的其他问题)所使用的 CNN 架构在本质上是相同的。 唯一真正的不同是,在 CNN 层完成特征提取之后会发生什么。 例如,一个差异可能是用于不同任务的损失函数,如下图所示:
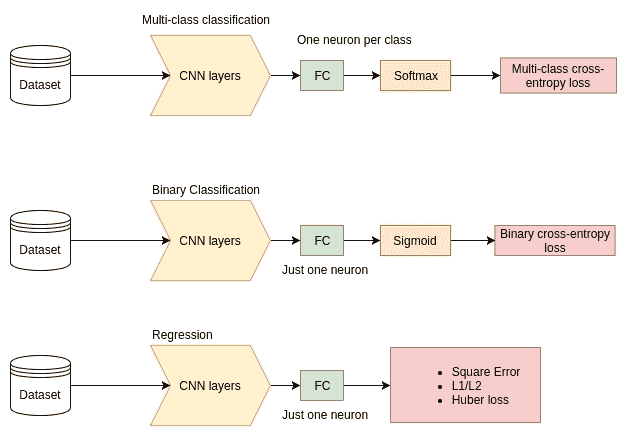
当我们着眼于 CNN 可以解决的各种问题时,您会在本书中看到重复出现的模式。 显然,可以使用 CNN 从输入数据中提取一些有意义的特征向量来解决许多涉及图像的任务,然后根据任务以某种方式对其进行处理并将其馈入不同的损失函数。 现在,让我们通过查看常用的损失函数来开始并专注于图像分类任务。
交叉熵损失(对数损失)
图像分类的最简单形式是二分类。 在这里,我们有一个分类器,该分类器只有一个要分类的对象,例如狗/不是狗。 在这种情况下,我们可能使用的损失函数是二元交叉熵损失。
真实标签p与模型预测q之间的交叉熵函数定义为:

i是我们标签和预测的每个可能元素的索引。
但是,当我们处理只有两个可能结果y = 1和y = 0的二元情况时,可以简化p ∈ {y, 1-y}和q ∈ {y_hat, 1-y_hat}我们得到:
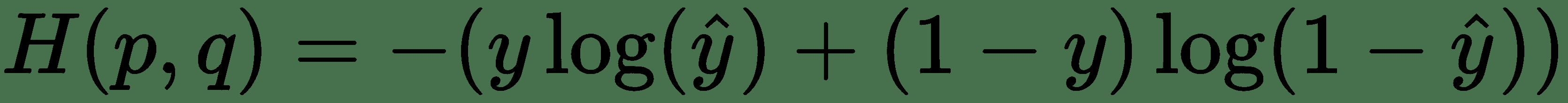
这是等效的
迭代m训练示例,将要最小化的成本函数L变为:

这在直觉上是正确的,因为当y=1时,我们要最小化L(y, y_hat) = - log(y_hat),需要最大化y_hat;当y=0时,我们要最小化L(y, y_hat) = - log(1 - y_hat),需要最小化y_hat。
在 TensorFlow 中,可以在tf.losses模块中找到二元交叉熵损失。 知道我们模型的原始输出y_hat的名称是logits很有用。 在将其传递给交叉熵损失之前,我们需要对其应用 Sigmoid 函数,以便我们的输出在 0 到 1 之间缩放。TensorFlow 实际上将所有这些步骤组合为一个操作,如下面的代码。 TensorFlow 还将为我们平均分批量损失。
loss = tf.losses.sigmoid_cross_entropy(multi_class_labels=labels_in, logits=model_prediction)
多类交叉熵损失
多类交叉熵损失用于多类分类中,例如第 2 章,“深度学习和卷积神经网络”中的 MNIST 数字分类问题。 像上面一样,我们使用交叉熵函数,经过几次计算,我们为每个训练示例获得了多类交叉熵损失L:

在此,y^(k)为 0 或 1,表示类别标签k是否是用于预测y_hat^(k)的正确分类。 要使用此损失,我们首先需要向模型中最终 FC 层的输出y_hat添加 softmax 激活。 交叉熵与 softmax 的组合如下所示:
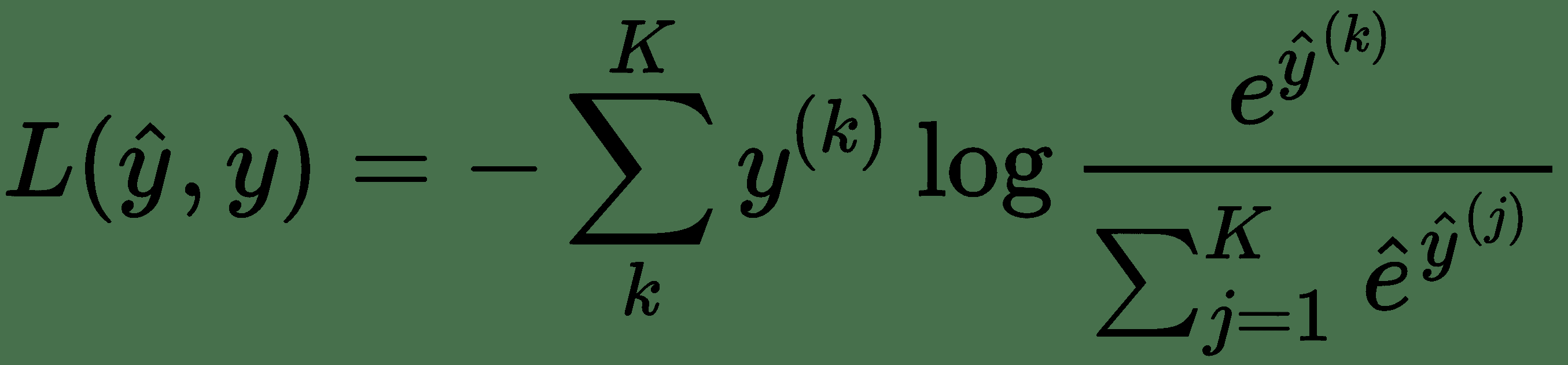
知道我们模型的原始输出y_hat的名称是logits很有用。 对率是传递给 softmax 函数的内容。 softmax 函数是 Sigmoid 函数的多类版本。 一旦通过 softmax 函数,我们就可以使用我们的多类交叉熵损失。 TensorFlow 实际上将所有这些步骤组合为一个操作,如下所示:
loss = tf.reduce_mean(tf.nn.softmax_cross_entropy_with_logits(logits=model_logits, labels=labels_in))
我们必须使用tf.reduce_mean,因为我们将获得批次中每个图像的损失值。 我们使用tf.reduce_mean来获取批次的平均损失。
我们可以像上面一样再次使用tf.losses模块,特别是tf.losses.softmax_cross_entropy模块,然后我们不需要tf.reduce_mean,但我们决定向您展示一种不同的方式,以便您可以看到,在 TensorFlow 中也有很多方法可以使用。 随着 TensorFlow 的发展,实现相同结果的不同方法也越来越多,而且通常没有比其他方法差很多的方法。
训练/测试数据集拆分
暂时请注意,我们需要将数据集分为两组:训练和测试。 正如第 1 章,“TensorFlow 简介和设置”中所述,这是因为我们需要以某种方式检查模型是否能够从其自身的训练样本中进行泛化(是否能够正确识别训练中从未见过的图像)。 如果我们的模型不能做到这一点,对我们来说就没有太大用处。
还有一些其他要记住的重要点:
- 训练和测试数据必须来自相同的分布(因此在拆分之前合并并混洗所有数据)
- 训练集通常大于测试集(例如,训练:占总数的 70%,测试:占总数的 30%)。
对于我们在前几章中要处理的示例,这些基础知识就足够了,但是在随后的章节中,我们将更详细地介绍如何为大型项目正确设置数据集。
数据集
在本节中,我们将讨论图像分类中使用的最重要和最著名的最新数据集。 这是必要的,因为对计算机视觉的任何细读都可能与它们重叠(包括本书!)。 在卷积神经网络到来之前,研究界在图像分类比赛中使用的两个主要数据集是 Caltech 和 PASCAL 数据集。
加州理工学院的数据集由加州理工学院建立,并发布了两个版本。 Caltech-101 于 2003 年发布,包含 101 个类别,每个类别约 40 至 800 张图像; Caltech-256 于 2007 年发布,具有 256 个对象类别,总共包含 30607 张图像。 这些图片是从 Google 图片和 PicSearch 收集的,其大小约为300x400像素。
Pascal 视觉对象类(VOC)挑战成立于 2005 年。每年组织到 2012 年,它为图像分类,对象检测,分割和操作分类提供了广泛的自然图像的著名基准数据集。 它是一个多样化的数据集,包含来自各种大小,姿势,方向,照明和遮挡的 flickr 的图像。 从 2005 年(仅四个类别:自行车,汽车,摩托车和人,训练/验证/测试:包含 5 个图像的 2578 个注释对象的 1578 张图像)到 2012 年(二十个类别,训练/验证数据具有 11,530 张图片,包含 27,450 个 ROI 注释对象和 6,929 个分割)。
重大变化来自 PASCAL(VOC)2007 挑战赛,当时类的数量从 4 个增加到 20 个,并且此后一直固定。 分类任务的评估指标已更改为平均精度。 仅在 VOC 2007 挑战赛之前提供测试数据的注释。
随着更复杂的分类方法的出现,前面的数据集是不够的,以下几节中介绍的 ImageNet 数据集和 CIFAR 数据集成为分类测试的新标准。
ImageNet
ImageNet 数据集由 Alex Berg(哥伦比亚大学),Jia Deng(普林斯顿大学)和 Lii-Fei Li(斯坦福大学)在 2010 年共同创建,旨在进行大规模视觉识别的测试比赛, PASCAL 可视对象类挑战,2010 年。数据集是代表 WordNet 内容的图像的集合。 WordNet 是英语的词汇数据库。 它以分层结构将英语单词分成称为同义词集的同义词集。 以下屏幕截图显示了名词的 WordNet 结构。 括号中的数字是子树中的同义词集的数量。

图像分类算法的发展几乎解决了现有数据集上的分类难题,因此需要一个新的数据集,以实现大规模图像分类。 这更接近现实情况,在这种情况下,我们希望机器描述模拟人的能力的任意图像的内容。 与上一代产品的分类数量在 100 年代相比,ImageNet 提供了超过 1000 万个高质量图像,覆盖了 10,000 多个类。 这些类别中的许多类别是相互关联的,这使分类任务更具挑战性,例如,区分许多品种的狗。 由于数据集非常庞大,因此很难使用其中存在的所有类别对每个图像进行注释,因此按照惯例,每个图像仅被标记为一个类别。
自 2010 年以来,一年一度的 ImageNet 大规模视觉识别挑战赛(ILSVRC)挑战集中于图像分类,单对象定位和检测。 对象分类挑战的数据包括 120 万张图像(来自 1000 个类别/同义词),训练数据,50,000 张验证数据图像和 100,000 张测试数据图像。
在分类挑战中,用于评估算法的主要指标是前 5 位错误率。 该算法允许给出五个预测类别,并且如果至少一个预测类别与真实情况标签匹配,则不会受到惩罚。
正式地,如果我们让i为图像,让C[i]为真实情况标签。 然后,我们有了预测的标签c[ij], j ∈ [1, 5],其中至少一个等于C[i]才能将其视为成功的预测。 考虑预测误差如下:

那么,算法的最终误差就是测试图像上出错的比例,如下所示:
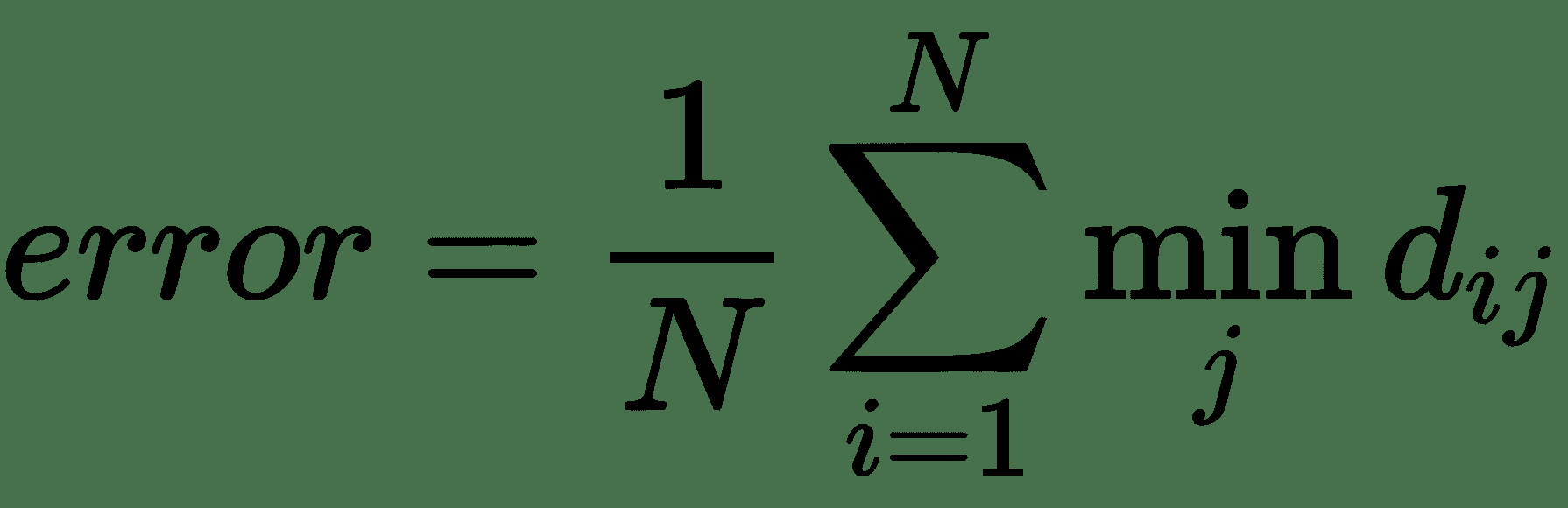
Imagenet 是近年来深度学习蓬勃发展的主要原因之一。 在深度学习开始流行之前,ILSVRC 的前五位错误率大约为 28%,并且丝毫没有下降太多。 但是,在 2012 年,挑战赛的冠军 SuperVision 将前 5 名的分类错误率降低到了 16.4%。 团队模型(现在称为 AlexNet)是一个深度卷积神经网络。 这项巨大的胜利唤醒了人们使用 CNN 的力量,它成为许多现代 CNN 架构的垫脚石。
在接下来的几年中,CNN 模型继续占主导地位,前 5 个错误率持续下降。 2014 年冠军 GoogLeNet 将错误率降低到 6.7%,而 ResNet 在 2015 年将错误率再次降低了一半,降至 3.57%。 此后,2017 年的赢家“WMW 挤压和激励网络”产生了 2.25% 的误差,出现了较小的改进。
CIFAR
CIFAR-10 和 CIFAR-100 数据集是 Alex Krizhevsky,Vinod Nair 和 Geoffrey Hinton 收集的小型(与现代标准相比)图像数据集。 这些数据集被研究界广泛用于图像分类任务。 它们被认为具有挑战性,因为图像质量非常低并且图像中的对象有时是部分可见的。 同时,由于图像较小,因此数据集很方便,因此研究人员可以快速在它们上产生结果。 CIFAR-100 增加了挑战,因为每个类别的图像数量很少,并且类别的数量也很大。 CIFAR10 和 CIFAR100 数据集每个包含 60,000 张图像。 两个数据集中的图像均为32x32x3 RGB 彩色图像。
在 CIFAR-10 中,有 10 个类别,每个类别有 6,000 张图像。 数据集分为 50,000 个训练图像和 10,000 个测试图像。 以下是 CIFAR-10 数据集的类列表和每个类的一些随机图像,因此您可以看到其外观:

CIFAR-100 具有 100 个类别,每个类别 600 张图像。 这 100 个类别分为 20 个超类。 每个图像都有一个精细标签(它属于的类)和一个粗糙标签(它属于的超类)。 CIFAR-100 中的类和超类的列表可在这个页面中找到。 将类别的数量从粗糙(20)增加到精细(100)有助于最大程度地提高类别间的可变性。 这意味着我们希望模型考虑图像中两个看起来相似的对象属于不同的类。 例如,一张床和一张沙发看起来相似但不完全相同,将它们放在单独的类中将确保它们与受训模型看起来不同。
CIFAR 的算法评估过程与 ImageNet 中的相同。 据 Saining Xie 等人报道,CIFAR-10 的报告最好的 top-1 误差为 3.58%,而 CIFAR-100 的误差为 17.31%。 深入神经网络的聚合残差转换中,他们介绍了新颖的 ResNeXt 架构。 可以在这里和这里找到在 CIFAR-10 和 CIFAR-100 上将深度学习结果用于图像分类的最新技术。
加载 CIFAR
可以从前面提到的 Python,Matlab 和二进制版本的官方网站下载数据集。 有多种加载和读取这些数据集的方法。 实际上,在我们的 TensorFlow 实现中,我们使用 Keras 库加载它,该库现在是tf.keras模块中 TensorFlow 的一部分。 在这里,我们提供了一些示例代码来加载 CIFAR-10 数据集,但是 CIFAR-100 数据集的加载方式几乎相同:
import tensorflow as tf
from tf.keras.datasets import cifar10
(x_train, y_train), (x_test, y_test) = cifar10.load_data()
print('x_train shape:',x_train.shape)
print('y_train shape:',y_train.shape)
print('x_test shape:',x_test.shape)
print('y_test shape:',y_test.shape)
print('x_train.shape[0]:',training samples)
print('x_test.shape[0]:',test samples)
# Convert class vectors to binary class matrices
y_train = tf.keras.utils.to_categorical(y_train,10)
y_test = tf.keras.utils.to_categorical(y_test,10)
此代码返回两个元组:
x_train, x_test: uint8 array of RGB image data with shape (num_samples, 3, 32, 32)
y_train, y_test: uint8 array of category labels (integers in range 0-9) with shape (num_samples,)
前面代码的打印语句的输出如下:
x_train shape:(50000,32,32,3
y_train shape:(50000,1)
x_test shape:(10000,32,32,3)
y_test shape:(10000,1)
同样,使用以下命令加载 CIFAR-100 数据集:
from tf.keras.datasets import cifar100
(x_train, y_train), (x_test, y_test) = cifar100.load_data(label_mode='fine')
将 TensorFlow 用于图像分类
在本节中,我们将向您展示如何实现相对简单的 CNN 架构。 我们还将研究如何训练它对 CIFAR-10 数据集进行分类。
首先导入所有必需的库:
import fire
import numpy as np
import os
import tensorflow as tf
from tf.keras.datasets import cifar10
我们将定义一个将实现训练过程的 Python 类。 类名是Train,它实现两种方法:build_graph和train。 当执行主程序时,将触发train功能:
class Train:
__x_ = []
__y_ = []
__logits = []
__loss = []
__train_step = []
__merged_summary_op = []
__saver = []
__session = []
__writer = []
__is_training = []
__loss_val = []
__train_summary = []
__val_summary = []
def __init__(self):
pass
def build_graph(self):
[...]
def train(self, save_dir='./save', batch_size=500):
[...]
if __name__ == '__main__':
cnn= Train()
cnn.train
建立 CNN 图
让我们通过build_graph函数进行详细介绍,该函数包含网络定义,损失函数和所使用的优化器。 首先,我们通过为输入定义占位符来启动函数。 我们将使用两个占位符在图中提供数据和标签:__x_和__y_。 占位符__x_将保存我们输入的 RGB 图像,而占位符__y_ 存储一个对应类别的热门标签。 在定义占位符形状的N部分时,我们使用None,因为这告诉 TensorFlow 该值可以是任何值,并且在执行图时将提供该值:
def build_graph(self):
self.__x_ = tf.placeholder("float", shape=[None, 32, 32, 3], name='X')
self.__y_ = tf.placeholder("int32", shape=[None, 10], name='Y')
self.__is_training = tf.placeholder(tf.bool)
然后,我们将在name_scope模型中定义我们的网络。 Name_scope返回定义 TensorFlow 操作时使用的上下文管理器。 该上下文管理器验证变量是否来自同一图,将该图设为默认图,并在该图中推送名称范围。
对于此模型,我们将构建一个具有三个卷积层,三个池化层和两个完全连接层的简单 CNN。 我们使用tf.layers API 来构建 CNN 层。 tf.reshape函数将张量从最后一个池化层重塑为一维张量,以匹配密集层期望接收的量。 最后一层的输出分配给self.__logits,它是将作为输入传递到我们的损失函数的张量:
with tf.name_scope("model") as scope:
conv1 = tf.layers.conv2d(inputs=self.__x_, filters=64, kernel_size=[5, 5],
padding="same", activation=tf.nn.relu)
pool1 = tf.layers.max_pooling2d(inputs=conv1, pool_size=[2, 2], strides=2)
conv2 = tf.layers.conv2d(inputs=pool1, filters=64, kernel_size=[5, 5],
padding="same", activation=tf.nn.relu)
pool2 = tf.layers.max_pooling2d(inputs=conv2, pool_size=[2, 2], strides=2)
conv3 = tf.layers.conv2d(inputs=pool2, filters=32, kernel_size=[5, 5],
padding="same", activation=tf.nn.relu)
pool3 = tf.layers.max_pooling2d(inputs=conv3, pool_size=[2, 2], strides=2)
pool3_flat = tf.reshape(pool3, [-1, 4 * 4 * 32])
# FC layers
FC1 = tf.layers.dense(inputs=pool3_flat, units=128, activation=tf.nn.relu)
FC2 = tf.layers.dense(inputs=FC1, units=64, activation=tf.nn.relu)
self.__logits = tf.layers.dense(inputs=FC2, units=10)
下一步是在名称范围loss_func中定义损失函数。 此处使用的损失函数是 softmax 交叉熵,如前所述,我们使用tf.reduce_mean对整个批次的损失进行平均。 我们创建变量来保存训练loss __loss和验证损失__loss_val,并将这些标量添加到 TensorFlow 摘要数据中,以便稍后在 TensorBoard 中显示:
with tf.name_scope("loss_func") as scope:
self.__loss = tf.reduce_mean(tf.nn.softmax_cross_entropy_with_logits(logits=self.__logits,
labels=self.__y_))
self.__loss_val = tf.reduce_mean(tf.nn.softmax_cross_entropy_with_logits(logits=self.__logits,
labels=self.__y_))
# Add loss to tensorboard
self.__train_summary = tf.summary.scalar("loss_train", self.__loss)
self.__val_summary = tf.summary.scalar("loss_val", self.__loss_val)
定义模型和损失函数后,我们需要指定将用于最小化损失的优化函数。 我们在这里选择的优化函数是 Adam 优化器,它在名称范围优化器中定义。
学习率调度
在上一章中,我们简要提到了在训练过程中保持恒定的学习率可能会出现的问题。 随着我们模型的开始学习,我们的初始学习率很可能会变得太大而无法继续学习。 梯度下降更新将开始超出或绕过我们的最小值; 结果,损失函数的值不会降低。 为了解决这个问题,我们可以不时降低学习率的值。 这个过程称为学习率调度,有几种流行的方法。
第一种方法是在训练过程中的固定时间步长(例如,当训练完成 33% 和 66% 时)降低学习率。 通常,当达到这些设置时间时,您会将学习率降低 10 倍。
第二种方法涉及根据时间步长的指数或二次函数降低学习率。 可以执行此操作的函数的示例如下:
decayed_learning_rate = learning_rate * decay_rate ^ (global_step / decay_steps)
通过使用这种方法,学习率会随着训练时间的推移而平稳降低。
最后一种方法是使用我们的验证集,并查看验证集上的当前准确率。 在验证准确率不断提高的同时,我们对学习率无能为力。 一旦验证准确率停止增加,我们就将学习率降低某种程度。 重复此过程,直到训练结束。
所有方法都可以产生良好的结果,当您进行训练以查看哪种方法更适合您时,可能值得尝试所有这些不同的方法。 对于此特定模型,我们将使用第二种方法,即学习率呈指数衰减。 我们使用 TensorFlow 操作tf.train.exponential_decay来执行此操作,该操作遵循前面显示的公式。 作为输入,它采用当前的学习率,全局步长,衰减之前的步数和衰减率。
在每次迭代中,当前的学习率都会提供给我们的 Adam 优化器,后者使用minimize函数,该函数使用梯度下降来使损失最小化并将global_step变量增加 1。 最后,在训练期间,将learning_rate和global_step添加到摘要数据以在 TensorBoard 上显示:
with tf.name_scope("optimizer") as scope:
global_step = tf.Variable(0, trainable=False)
starter_learning_rate = 1e-3
# decay every 10000 steps with a base of 0.96 function
learning_rate = tf.train.exponential_decay(starter_learning_rate, global_step,
1000, 0.9, staircase=True)
self.__train_step = tf.train.AdamOptimizer(learning_rate).minimize(self.__loss,
global_step=global_step)
tf.summary.scalar("learning_rate", learning_rate)
tf.summary.scalar("global_step", global_step)
尽管 Adam 优化器会自动为我们调整和降低学习率,但我们仍然发现,采用某种形式的学习率调度也可以改善结果。
一旦定义了图的所有组件,就将图中收集的所有摘要合并到__merged_summary_op中,并通过tf.global_variables_initializer()初始化图的所有变量。
自然,在训练模型时,我们希望将网络权重存储为二进制文件,以便我们可以将其加载回去以执行正向传播。 TensorFlow 中的那些二进制文件称为检查点,它们将变量名称映射到张量值。 要在检查点之间保存和还原变量,我们使用Saver类。 为避免填满磁盘,保护程序会自动管理检查点文件。 例如,他们每训练一次N小时,就只能保留N个最新文件或一个检查点。 在我们的例子中,我们将max_to_keep设置为None,这意味着将保留所有检查点文件:
# Merge op for tensorboard
self.__merged_summary_op = tf.summary.merge_all()
# Build graph
init = tf.global_variables_initializer()
# Saver for checkpoints
self.__saver = tf.train.Saver(max_to_keep=None)
另外,我们可以指定tf.GPUOptions要使用的 GPU 内存比例。 对象会话封装了执行操作和求值张量的环境。 创建FileWriter对象以将摘要和事件存储到文件后,__session.run(init)方法运行 TensorFlow 计算的一个步骤,方法运行必要的图片段来执行每个操作,并评估在init中初始化的每个张量作为图的一部分:
# Avoid allocating the whole memory
gpu_options = tf.GPUOptions(per_process_gpu_memory_fraction=0.6)
self.__session = tf.Session(config=tf.ConfigProto(gpu_options=gpu_options))
# Configure summary to output at given directory
self.__writer = tf.summary.FileWriter("./logs/cifar10", self.__session.graph)
self.__session.run(init)
tf.data API 简介
在继续之前,我们将看一下 TensorFlow 处理数据输入到我们可能训练的任何模型的方式。 TensorFlow tf.data API 为我们提供了轻松构建复杂的输入流水线可能需要的所有工具。 您可能通常会构建的一个流水线将涉及加载原始训练数据,对其进行一些预处理,改组,然后将其分批准备进行训练。 tf.data API 使我们能够使用简单且可重复使用的代码段轻松地完成所有这些步骤。
您需要了解tf.data API 的两个主要组件。 首先是tf.data.Dataset; 这就是您的原始数据。 更具体地说,它包含一系列元素,其中每个元素包含一个或多个张量对象。 对于图像分类任务,一个元素将是一个训练示例,并且它将由两个张量组成-一个张量用于图像,一个张量用于其相应的标签。
第二个成分是tf.data.Iterator。 这些允许您从数据集中提取元素,并充当数据集和模型代码之间的连接。 TensorFlow 中有几种不同类型的迭代器,它们都有不同的用途,涉及不同的使用难度。
创建数据集可以通过两种方式完成。 第一种方法是通过创建数据源。 一个简单的例子是使用tf.data.Dataset.from_tensor_slices(),它将根据一个或多个张量对象的切片创建一个数据集。 产生数据集的另一种方法是在现有数据集上使用数据集转换。 这样做将返回合并了所应用转换的新数据集。 重要的是要了解所有输入流水线必须以数据源开头。 一旦有了Dataset对象,通常对它应用所有链接在一起的多个转换。
目前,一些简单的转换示例包括Dataset.batch()和Dataset.repeat(),它们从Dataset对象返回一批具有指定大小的批次,当Dataset内容到达末尾时,它将继续重复该内容。 一种可以多次遍历数据集的简单方法(count参数)。
现在我们已经建立了数据集,我们可以使用tf.data.Iterators进行迭代并从中提取元素。 同样,有几种不同的迭代器可供使用,但是我们将使用的最简单的迭代器是一发迭代器。 该迭代器仅支持一次浏览数据集,但是设置非常简单。 我们通过在数据集上调用make_one_shot_iterator()方法并将结果分配给变量来创建它。 然后,我们可以在创建的迭代器上调用get_next(),并将其分配给另一个变量。
现在,无论何时在会话中运行此操作,我们都将遍历数据集一次,并将提取一个新批次以使用:
def train(self, save_dir='./save', batch_size=500):
# Use keras to load the complete cifar dataset on memory (Not scalable)
(x_train, y_train), (x_test, y_test) = cifar10.load_data()
# Convert class vectors to binary class matrices.
y_train = tf.keras.utils.to_categorical(y_train, 10)
y_test = tf.keras.utils.to_categorical(y_test, 10)
# Using Tensorflow data Api to handle batches
dataset_train = tf.data.Dataset.from_tensor_slices((x_train, y_train))
dataset_train = dataset_train.shuffle(buffer_size=10000)
dataset_train = dataset_train.repeat()
dataset_train = dataset_train.batch(batch_size)
dataset_test = tf.data.Dataset.from_tensor_slices((x_test, y_test))
dataset_test = dataset_test.repeat()
dataset_test = dataset_test.batch(batch_size)
# Create an iterator
iter_train = dataset_train.make_one_shot_iterator()
iter_train_op = iter_train.get_next()
iter_test = dataset_test.make_one_shot_iterator()
iter_test_op = iter_test.get_next()
# Build model graph
self.build_graph()
主要训练循环
一旦检索到数据并构建了图,就可以开始我们的主要训练循环,该循环将继续进行 20,000 多次迭代。 在每次迭代中,都使用 CPU 设备获取一批训练数据,并调用AdamOptimizer对象的__train_step.run方法向前运行一次,向后运行一次。 每进行 100 次迭代,我们就会对当前的训练和测试批次进行一次前向传递,以收集训练和验证损失以及其他汇总数据。 然后,FileWriter对象的add_summary方法将提供的 TensorFlow 摘要:summary_1和summary_2包装在事件协议缓冲区中,并将其添加到事件文件中:
# Train Loop
for i in range(20000):
batch_train = self.__session.run([iter_train_op])
batch_x_train, batch_y_train = batch_train[0]
# Print loss from time to time
if i % 100 == 0:
batch_test = self.__session.run([iter_test_op])
batch_x_test, batch_y_test = batch_test[0]
loss_train, summary_1 = self.__session.run([self.__loss, self.__merged_summary_op],
feed_dict={self.__x_: batch_x_train,
self.__y_: batch_y_train, self.__is_training: True})
loss_val, summary_2 = self.__session.run([self.__loss_val, self.__val_summary],
feed_dict={self.__x_: batch_x_test,
self.__y_: batch_y_test, self.__is_training: False})
print("Loss Train: {0} Loss Val: {1}".format(loss_train, loss_val))
# Write to tensorboard summary
self.__writer.add_summary(summary_1, i)
self.__writer.add_summary(summary_2, i)
# Execute train op
self.__train_step.run(session=self.__session, feed_dict={
self.__x_: batch_x_train, self.__y_: batch_y_train, self.__is_training: True})
训练循环结束后,我们将最终模型存储在带有op __saver.save的检查点文件中:
# Save model
if not os.path.exists(save_dir):
os.makedirs(save_dir)
checkpoint_path = os.path.join(save_dir, "model")
filename = self.__saver.save(self.__session, checkpoint_path)
print("Model saved in file: %s" % filename)
模型初始化
随着我们向模型中添加越来越多的层,使用反向传播训练它们的难度越来越大。 通过模型传递回去以更新权重的误差值随着我们的深入而变得越来越小。 这被称为消失梯度问题。
因此,在开始训练模型之前,需要注意的重要一件事是将权重初始化为什么值。 错误的初始化会使模型收敛非常慢,或者甚至根本不会收敛。
尽管我们不确切知道训练后我们的权重最终会变成什么样的值,但我们可以合理地预期,其中的一半将为正值,而另一半将为负值。
不要用零初始化所有权重
现在,我们可能倾向于认为将所有权重设置为零将实现最大的对称性。 但是,这实际上是一个非常糟糕的主意,并且我们的模型永远不会学到任何东西。 这是因为当您进行前向通过时,每个神经元都会产生相同的结果。 因此,在反向传播步骤中,所有权重将以相同的方式更新。 这意味着模型永远无法学习丰富的功能,因此请不要像这样初始化。
用均值为零的分布初始化
一个更好的主意是使用所有以零为中心的较小随机值初始化权重。 为此,我们可以使用均值为零和单位方差为零的正态分布的随机值,然后将其按某个较小的值进行缩放,例如 0.01。
这样做会破坏权重的对称性,因为它们都是随机且唯一的,这是一件好事。 计算向前和向后通过时,我们的模型神经元现在将以不同的方式进行更新。 这将使他们有机会学习许多不同的功能,这些功能将作为大型神经网络的一部分协同工作。
然后唯一需要担心的是我们设定的权重值有多小。 如果设置得太小,反向传播更新也将非常小,这可能会在更深层的网络中消失梯度问题。
下图显示了权重的要求之一(零均值):
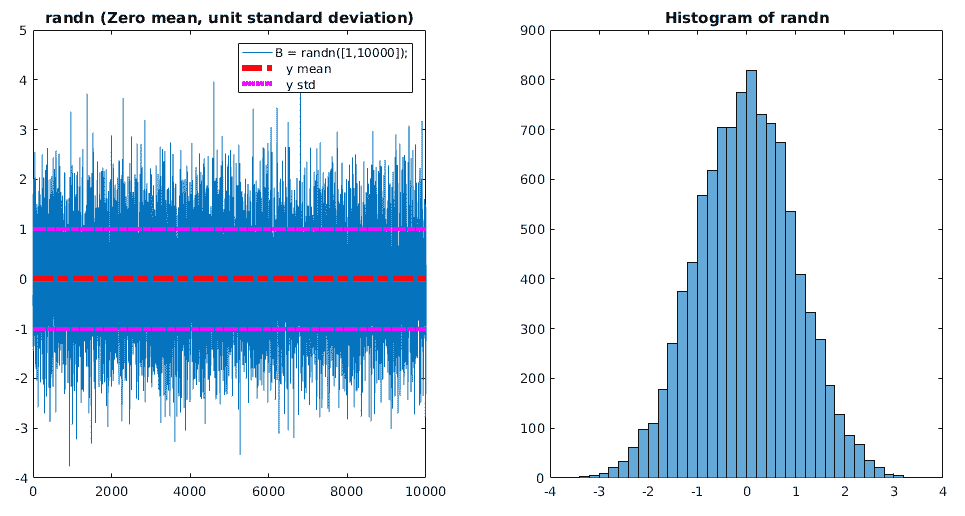
Xavier-Bengio 和初始化器
在了解训练深度前馈神经网络的难度时,Xavier Glorot 和 Yoshua Bengio 表明,如果从均匀分布U ~ [-1/√n, 1/√n]初始化每一层的权重,其中n是上一层中的大小,对于 Sigmoid 激活函数,顶层(更靠近输出)的神经元迅速饱和为 0。我们知道,由于 Sigmoid 函数的形式,激活值 0 表示权重非常大,并且反向传播的梯度接近零。 较小的梯度值会减慢学习过程,因为早期层中的权重停止更新或停止学习。
因此,我们想要的是使权重在最初确定的时间间隔内均匀分布,也就是说,权重的方差应该在我们从底层移动到顶层时保持不变。 这将使误差平稳地流到顶层,从而使网络在训练期间收敛更快。
为了实现这一点,Glorot 和 Bengio 证明了对于单位导数为 0 的对称激活函数f,每一层的权重方差必须如下:

在此,n[in]是到所讨论的层的单元数,n[out]是在下一层的单元数。 这意味着权重必须从以下均匀分布中采样:

我们还可以从零均值和前面的方差的正态分布中采样权重。 对于 ReLu 激活函数,He 等人证明了这一点。 方差应该改为:
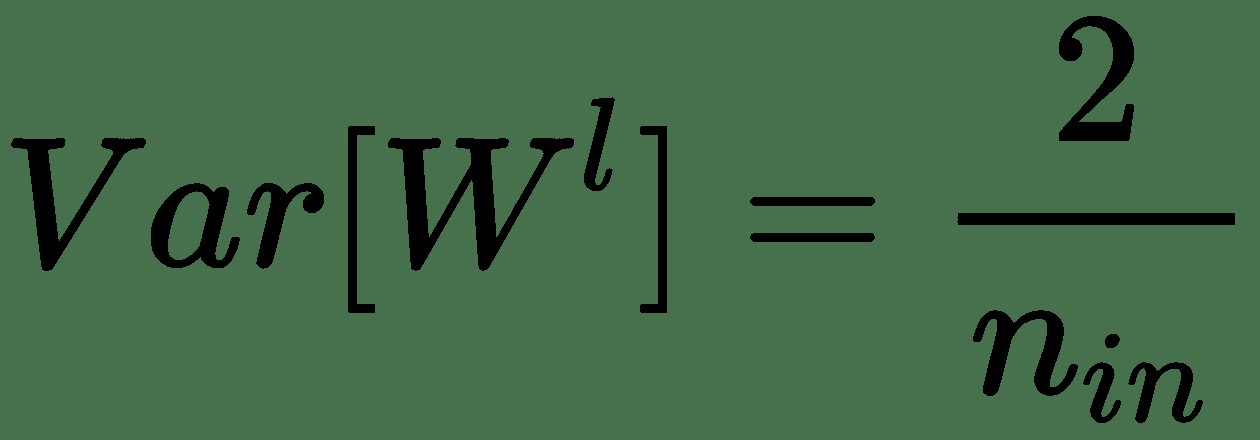 。
。
因此,作者使用零均值高斯分布初始化其权重,其标准差(STD)为√(2/n[in])。 然后将该初始化称为 He 初始化。
默认情况下,TensorFlow 的大部分tf.layers都使用 Glorot(xavier)初始化器,但是我们可以覆盖它并指定我们自己的初始化。 在这里,我们展示了一个如何覆盖conv2d层的默认初始化器的示例:
conv1 = tf.layers.conv2d(inputs=self.__x_, filters=64, kernel_size=[5, 5],
padding="same", activation=None,
kernel_initializer=tf.truncated_normal_initializer(stddev=0.01),
bias_initializer=tf.zeros_initializer())
通过规范化来提高泛化能力
到目前为止,在本章中,我们已经看到了如何使用 TensorFlow 训练卷积神经网络来完成图像分类任务。 训练完模型后,我们将其遍历测试集,并从一开始就将其存储起来,以查看其在从未见过的数据上的表现如何。 在测试集上评估模型的过程向我们表明了在部署模型时模型将泛化的程度。 能够很好地泛化的模型显然是理想的属性,因为它可以在许多情况下使用。
我们使用的 CNN 架构是可以提高模型泛化能力的方法之一。 要记住的一种简单技术是从设计模型开始就尽可能简单地使用很少的层或过滤器。 由于非常小的模型很可能无法适应您的数据,因此您可以慢慢增加复杂性,直到不再发生适应不足的情况为止。 如果您以这种方式设计模型,则将限制过拟合的可能性,因为您不允许自己拥有的模型对于数据集而言过大。
但是,在本节中,我们将探索我们可以做的其他一些事情,以建立更好的机器学习模型,以及如何将它们纳入我们的训练过程中。 以下方法旨在防止过拟合,并通过这样做,有助于创建更强大的模型,并能更好地进行泛化。 防止模型过拟合的过程称为正则化。
另一个可能也会发生并且看起来与过拟合非常相似的问题是,如果您的训练数据集没有捕获您想要分类的所有事物。 例如,如果您正在训练狗分类器,但是您的训练图像仅包含贵宾犬的图像。 如果要在 Labradors 上测试此训练有素的分类器,则可能无法分类。 这种数据不平衡是一个单独的问题,将在后面的章节中解决。
L2 和 L1 正则化
创建更强大模型的第一种方法是使用 L1 或 L2 正则化。 到目前为止,这些是最常见的正则化方法。 基本思想是在训练模型时,我们积极尝试使用这些权重的 L1 或 L2 范数对模型权重的值施加一些约束。
为此,我们在使用的任何损失函数中增加了一个额外的项。 对于 L1 正则化,我们添加的项是λ |w|,对于 L2 正则化,我们添加的项是0.5 λ w^2。 在前面的项中,w是我们网络中的所有权重,λ是称为正则化强度的超参数。 通过添加该项,我们可以防止权重值变得太大。
因此,为了 L1 正则化,第 1 章,“TensorFlow 简介和设置”的 SVM 损失函数,即:

变为:
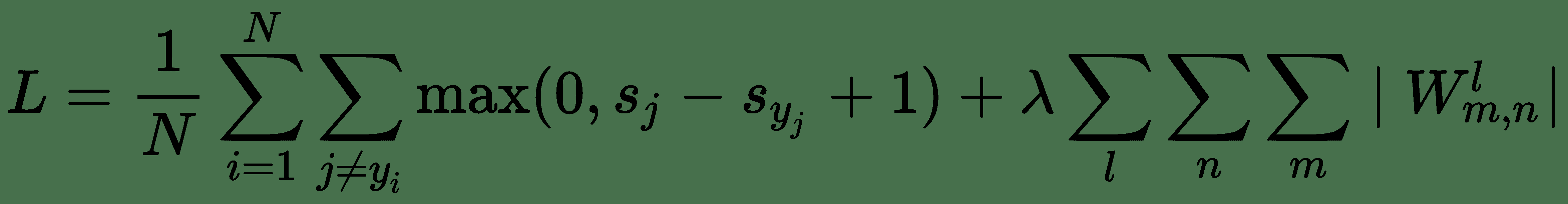
在这里,我们添加了对网络所有权重求和的正则化项。 此处,l是层索引,m, n是每一层的权重矩阵的索引。 L2 正则化的表达式看起来类似。
对于 L1 正则化,此额外项鼓励权重向量变得稀疏,这意味着许多权重值变为零。 结果,该模型变得不受噪声输入的影响,因为权重向量将仅使用重要输入的子集,这有助于避免过拟合。
对于 L2 正则化,除了保持权重之和较低之外,这个额外的项还强制权重值均匀分布在权重向量上,以便模型稍微使用所有权重,而不是大量使用权重。 由于输入和权重之间的乘法交互作用,从直觉上讲,这是一个理想的属性,可帮助模型避免过拟合。 L2 正则化有时也称为权重衰减; 这是因为在训练期间,您的所有权重都会因该项(L2 正则化项的导数)而线性减少或“衰减”。
请注意,在正则化期间我们不包括偏差项,而仅包括权重。 这是因为偏差项并不会真正影响模型的过拟合,因为它们以累加的方式影响输出,只是向上或向下移动而不是改变函数的形状。 包含它们没有害处,但是也没有好处,因此包含它们没有意义。
在下图中,您可能会注意到增加正则强度λ会减少过拟合。 高正则化项意味着网络变得接近线性,并且无法塑造复杂的决策边界。
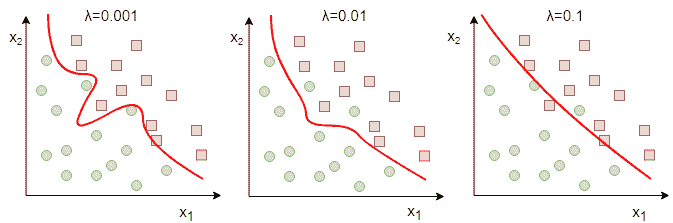
我们可以通过获取所有权重并对每个权重应用 l2 范数,然后将它们全部加在一起来手动实现 L2/L1 正则化,但是这对于大型模型来说很快就变得很乏味。 幸运的是,如果我们使用tf.layers,那么 TensorFlow 中有一种更简单的方法。 首先,我们设置了正则化器,如下所示:
l2_reg = tf.contrib.layers.l2_regularizer(scale=0.001)
scale参数是我们通常需要通过交叉验证找到并设置自己的λ。 如果将其设置为 0,则不会进行任何正则化。 现在,当我们创建任何层时,我们会将正则化函数作为参数传递。 TensorFlow 将进行计算以获取我们需要添加到损失函数中的所有正则化项:
# Example of adding passing regularizer to a conv layer.
reg_conv_layer = tf.layers.conv2d( inputs, filters, kernel_size, kernel_regularizer=l2_reg)
要添加我们的正则化项,我们首先需要将它们全部收集起来。 幸运的是,TensorFlow 会自动为我们将所有正则化项放到一个集合中,以便我们可以轻松访问它们。 TensorFlow 在tf.GraphKeys内存储一些与您创建的图相关的重要集合,例如可训练变量,汇总和正则化损失。 我们可以使用tf.get_collection()访问这些集合,并提供要获取的集合的名称。 例如,为了得到正则化损失,我们将编写以下内容:
reg_losses = tf.get_collection(tf.GraphKeys.REGULARIZATION_LOSSES)
这将返回一个列表,其中包含此集合中存储的所有张量。
您也可以使用tf.get_collection(key='my_collection')创建自己的集合,然后使用tf.add_to_collection(name='my_collection', value=some_variable_to_add)向其中添加变量。 如果使用提供的键已存在一个集合,则tf.get_collection将返回该集合而不是创建它。
现在我们有了正则化损失项,我们可以像这样将它们添加到我们通常的训练损失中,然后优化组合损失:
train_loss=[...] # Training loss
combined_loss = tf.n_add(train_loss, reg_losses)
退出
我们将要讨论的另一种用于正则化的技术是一种称为丢弃的东西。 丢弃法是由 G.E. Hinton 于 2012 年提出的,它是一种简单的正则化方法,可带来很好的效果。 丢弃法背后的想法是,在每次训练迭代中,一层中的所有神经元都可以以随机概率(通常为 50%)打开和关闭。
这种打开和关闭迫使网络学习与往常相同的概念,但是要通过多个不同的路径。 训练后,所有神经元都保持打开状态,这些路径的行为就像是多个网络的集合,用于平均最终结果,从而提高了泛化能力。 它迫使权重分布在整个网络中,并且像正则化一样将权重保持在较低水平。
理解这个概念的另一种方法是建立一个由多个人共享相似知识的团队。 他们每个人都会对如何解决特定问题有自己的想法,这些经验的结合提供了解决问题的更好方法:

在下图中,我们显示了模型测试误差。 显然,通过丢弃法,测试集上的误差会减少。 请记住,与所有正则化一样,与不使用正则化相比,使用丢弃法会使您的训练损失增加,但是到最后,我们只对模型测试错误率降低(泛化)感兴趣:
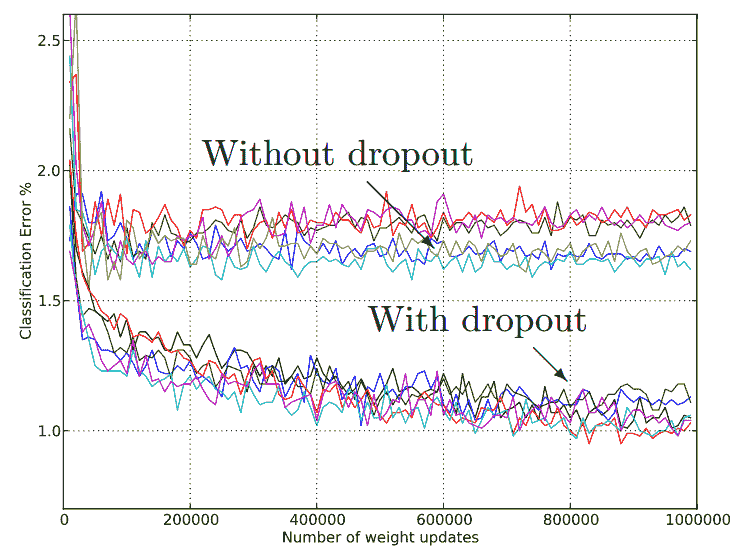
通常,丢弃法仅适用于全连接层,但也可以适用于卷积/池化层。 如果这样做,则将使用较低的p(掉线的可能性),接近 0.2。 同样,您将丢弃层放置在激活层之后。
要在 TensorFlow 模型中使用丢弃法,我们在希望将丢弃法应用到的输入层上调用tf.layers.dropout()。 我们还必须指定我们要使用的丢弃率,更重要的是,使用布尔值让 TensorFlow 知道我们的模型是否在训练中。 请记住,当我们在测试时使用模型时,我们会关闭丢弃,而这个布尔值将为我们做到这一点。 因此,带有丢弃的代码将如下所示:
# Fully connected layer (in tf contrib folder for now)
fc1 = tf.layers.dense(fc1, 1024)
# Apply Dropout (if is_training is False, dropout is not applied)
fc1 = tf.layers.dropout(fc1, rate=dropout, training=is_training)
批量规范层
之前,我们已经完成了权重的初始化工作,以使梯度下降优化器的工作更加轻松。 但是,好处仅在训练的早期阶段才能看到,并不能保证在后期阶段有所改善。 那就是我们转向另一个称为批量规范层的伟大发明的地方。 在 CNN 模型中使用批量规范层产生的效果与第 2 章,“深度学习和卷积神经网络”中看到的输入标准化大致相同。 现在唯一的区别是,这将在模型中所有卷积层和完全连接层的输出处发生。
批量规范层通常将附加到每个完全连接或卷积层的末端,但是在激活函数之前,它将对层输出进行规范化,如下图所示。 它通过获取层输出(一批激活)并减去批次平均值并除以批次标准差来执行此操作,因此层输出具有零均值和单位标准差。 请注意,在激活函数之前或之后放置批量规范化是一个引起激烈争论的话题,但是两者都应该起作用。

进行此标准化之后,批量规范层还具有两个可学习的参数,这些参数将按比例缩放标准化的激活并将其转移到模型认为最有助于其学习的内容。 整个过程通过消除消失的梯度问题来帮助训练。 反过来,这又允许模型在训练时使用更高的学习率,因此可以减少迭代次数。
在训练过程中,记录平均值和标准差值的移动平均值。 然后在测试时使用这些值,而不是计算批次统计信息。
批量规范层的一些优点如下:
- 改善梯度流动,允许训练更深层的网络(解决消失的梯度问题)
- 允许更高的学习率,使训练更快
- 减少对良好权重初始化的依赖(更简单的随机初始化)
- 给您的模型某种正则化效果
- 使得可以使用饱和非线性,例如 Sigmoid
对于更多的数学读者,可以在批量规范论文《批量规范化:通过减少内部协变量偏移来加速深层网络训练》中找到更为正式的定义,这是一篇写得很好的论文,易于理解和解释。 更详细的概念。 如果假设我们有一个仅具有全连接层的简单神经网络,则正如我们在第 1 章,“TensorFlow 简介和设置”中所看到的,每一层的激活将是s = f(x; W, b) = W · x + b表格。
假设g(·)是非线性的,例如 Sigmoid 或 ReLU,然后将批量归一化BN(·)直接应用于每个单元,例如:

在这里,可以忽略偏差,因为它将通过均值减法消除。 如果我们的批次大小为m,则标准化激活s[i]^(BN)的计算如下:
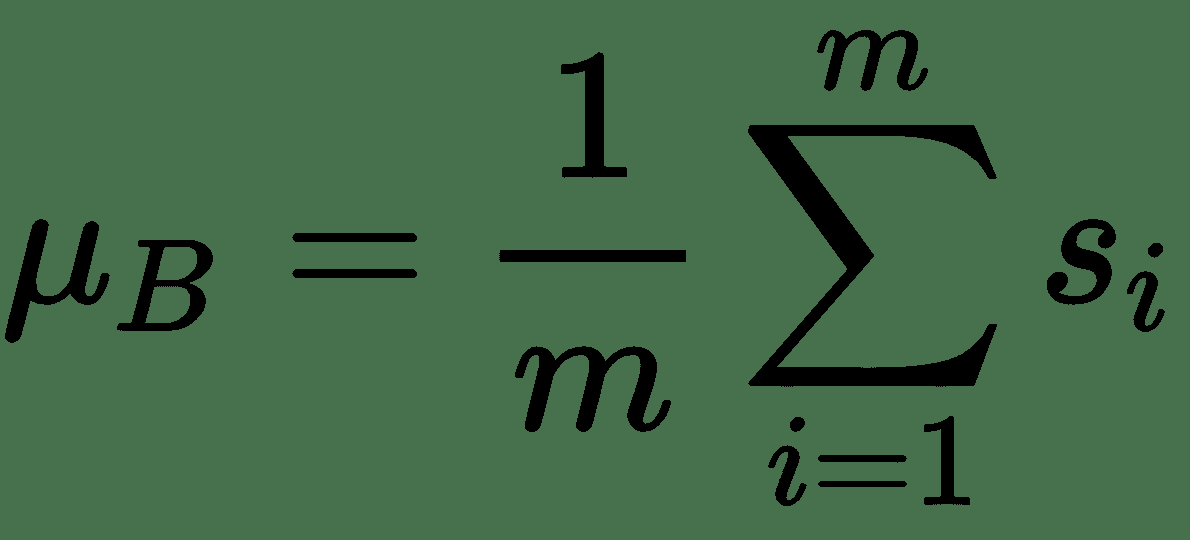
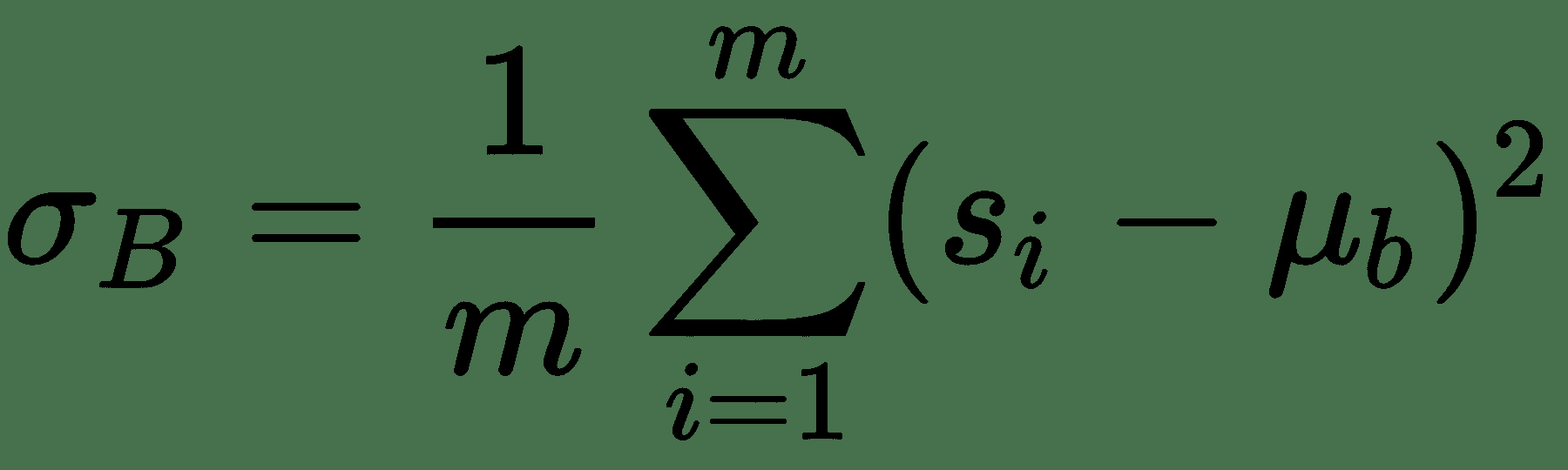
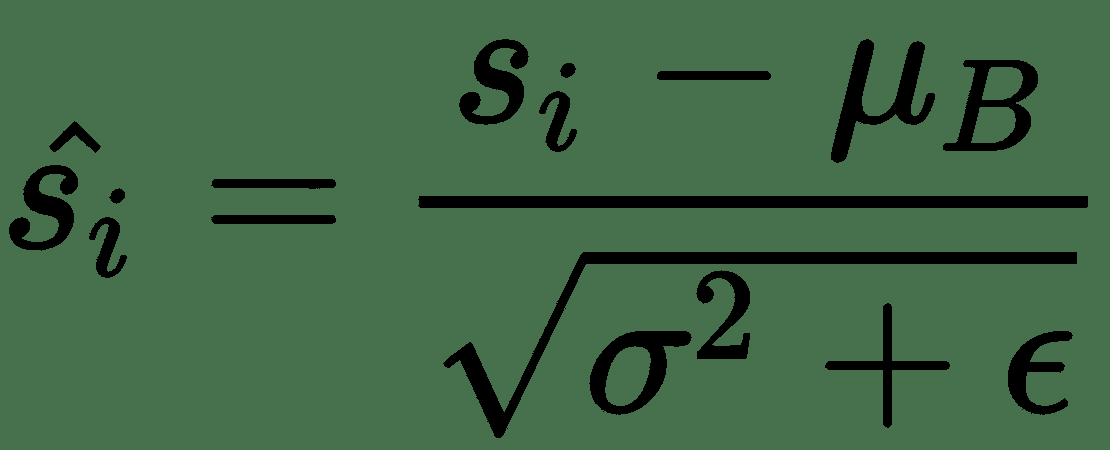
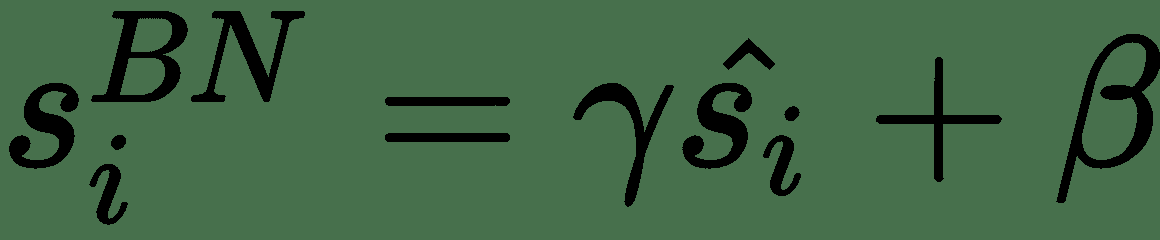
其中γ和β是可学习的参数,它们将缩放并移动您的标准化激活。 网络可以使用这些参数来决定是否需要标准化以及需要多少标准化。 这是正确的,因为如果我们设置β = μ和γ = √(δ^s + ε),则设置s[i]^(BN) = s[i]。
最后,这是一个如何在本章开始的分类示例代码中使用批量规范层的示例。 在这种情况下,我们将批量规范化层放在卷积层之后和激活函数之前:
conv3 = tf.layers.conv2d(inputs=pool2, filters=32, kernel_size=[5, 5],padding="same", activation=None)
conv3_bn = tf.layers.batch_normalization(inputs=conv3, axis=-1, momentum=0.9, epsilon=0.001, center=True,scale=True, training=self.__is_training, name='conv3_bn')
conv3_bn_relu = tf.nn.relu(conv3_bn)
pool3 = tf.layers.max_pooling2d(inputs=conv3_bn_relu, pool_size=[2, 2], strides=2)
总结
在本章中,我们了解了 CNN 模型的构建方式,包括使用哪些损失函数。 我们研究了 CIFAR 和互联网数据集,并了解了如何训练 CNN 来对 CIFAR10 数据集进行分类。 为此,我们被引入了 TensorFlow 数据 API,这使加载和转换数据的任务变得更加容易。 最后,我们讨论了通过谈论初始化和正则化的不同方法来提高训练模型的质量的方法。
在下一章中,我们将解决更困难的对象检测,语义和实例分割任务。
四、目标检测与分割
从上一章我们知道,当我们在输入图像中只有一个类的实例时,图像分类才真正处理这种情况。 即使那样,它也只能为我们提供粗略的输出,让我们知道图像中存在什么对象,但不知道它在哪里。 一个更有趣的情况是,当我们想查找一个类的所有实例,甚至多个不同的类在输入图像中的位置时。
为了解决这个更具挑战性的问题,需要进行对象检测和分割。 这些是计算机视觉领域,直到最近仍然非常具有挑战性。 然而,将卷积神经网络应用于这些问题近年来引起了很多关注,因此,在大多数情况下,现在可以考虑解决这些问题。 在本章中,我们将看到 CNN 如何很好地解决这些困难的任务。
下图显示了不同解决方案分段,定位,检测和实例分段之间的区别:

在开始讨论对象检测之前,我们需要了解另一个重要概念-定位。 它是改善分类和启用检测的关键构建块。 我们将看到这三个概念彼此密切相关,这是因为我们从图像分类到具有定位的分类,最后是对象检测。
在本章中,我们将学习以下有趣的主题:
- 图像分类与定位
- 对象检测
- 语义分割
- 实例分割
- 如何构建卷积神经网络来执行所有这些任务
图像分类与定位
在上一章学习了图像分类之后,我们现在知道对图像进行分类时,我们只是试图在该图像内输出对象的类标签。 通常,为了简化任务,图像中将只有一个对象。
展望未来,在许多情况下,我们也有兴趣在图像中找到对象的位置。 定位对象这一任务的名称称为定位。 在这种情况下,我们要产生的输出是围绕对象的盒子的坐标。 此框的名称是边界框或边界矩形。 关于定位的重要细节是,每个图像只能定位一个对象。
当我们建立一个负责预测类别标签以及感兴趣对象周围的边界框的模型时,称为带有局部化的图像分类。
作为回归的定位
可以使用与我们在第 3 章, “TensorFlow 中的图像分类”中了解的网络架构相似的网络架构来实现定位。
除了预测类标签外,我们还将输出一个标志,指示对象的存在以及对象边界框的坐标。 边界框坐标通常是四个数字,分别代表左上角的x和y坐标,以及框的高度和宽度。
例如,在这种情况下,我们有两个类别(C1(汽车)和 C2(人))进行预测。 我们网络的输出如下所示:

该模型的工作原理如下:
- 我们将输入图像输入到 CNN。
- CNN 产生一个特征向量,该特征向量被馈送到三个不同的 FC 层。 这些不同的 FC 层(或负责人)中的每一个都将负责预测不同的事物:对象存在,对象位置或对象类。
- 训练中使用了三种不同的损失:每个头部一个。
- 计算当前训练批次的比率,以权衡给定对象的存在对分类和位置损失的影响。 例如,如果批次中只有 10% 的对象图像,那么这些损失将乘以 0.1。
提醒一下:输出数字(即 4 个边界框坐标)称为回归。
请注意,分类和回归之间的重要区别是分类时,我们获得离散/分类输出,而回归提供连续值作为输出。 我们在图中显示模型如下:

从图中可以清楚地看到三个全连接层,每个层都输出不同的损失(状态,类和框)。 使用的损失是逻辑回归/对数损失,交叉熵/ softmax 损失和 Huber 损失。 胡贝尔损失是我们从未见过的损失。 这是用于回归的损失,是 L1 和 L2 损失的一种组合。
局部化的回归损失给出了图像中对象的真实情况边界框坐标与模型预测的边界框坐标之间的某种相似度度量。 我们在这里使用 Huber 损失,但是可以使用各种不同的损失函数,例如 L2,L1 或平滑 L1 损失。
分类损失和局部损失被合并并通过标量比加权。 此处的想法是,如果首先存在一个对象,则我们只对反向传播分类和边界框损失感兴趣。
此模型的完整损失公式如下:

TensorFlow 实现
现在,我们将介绍如何在 TensorFlow 中实现这种模型。 它与分类模型极为相似,不同之处在于,我们在末尾有多个输出层而不是只有一个,并且每个层都有自己的损失函数:
def build_graph(self):
self.__x_ = tf.placeholder("float", shape=[None, 240, 320, 3], name='X')
self.__y_box = tf.placeholder("float", shape=[None, 4], name='Y_box')
self.__y_obj = tf.placeholder("float", shape=[None, 1], name='Y_obj')
# Training flag for dropout in the fully connected layers
self.__is_training = tf.placeholder(tf.bool)
with tf.name_scope("model") as scope:
conv1 = tf.layers.conv2d(inputs=self.__x_, filters=32, kernel_size=[5, 5], padding="same", activation=tf.nn.relu)
pool1 = tf.layers.max_pooling2d(inputs=conv1, pool_size=[2, 2], strides=2)
conv2 = tf.layers.conv2d(inputs=pool1, filters=64, kernel_size=[5, 5], padding="same", activation=tf.nn.relu)
pool2 = tf.layers.max_pooling2d(inputs=conv2, pool_size=[2, 2], strides=2)
conv3 = tf.layers.conv2d(inputs=pool2, filters=32, kernel_size=[5, 5], padding="same", activation=tf.nn.relu)
pool3 = tf.layers.max_pooling2d(inputs=conv3, pool_size=[2, 2], strides=2)
pool3_flat = tf.reshape(pool3, [-1, 40 * 30 * 32])
# 2 Head version (has object head, and bounding box)
self.__model_box = tf.layers.dense(inputs=pool3_flat, units=4)
self.__model_has_obj = tf.layers.dense(inputs=pool3_flat, units=1, activation=tf.nn.sigmoid)
with tf.name_scope("loss_func") as scope:
loss_obj = tf.losses.log_loss(labels=self.__y_obj, predictions=self.__model_has_obj)
loss_bbox = tf.losses.huber_loss(labels=self.__y_box, predictions=self.__model_box)
# Get ratio of samples with objects
batch_size = tf.cast(tf.shape(self.__y_obj)[0], tf.float32)
num_objects_label = tf.cast(tf.count_nonzero(tf.cast(self.__y_obj > 0.0, tf.float32)), tf.float32)
ratio_has_objects = (num_objects_label * tf.constant(100.0)) / batch_size
# Loss function that has an "ignore" factor on the bbox loss when objects is not detected
self.__loss = loss_obj + (loss_bbox*ratio_has_objects)
# Add loss to tensorboard
tf.summary.scalar("loss", self.__loss)
tf.summary.scalar("loss_bbox", loss_bbox)
tf.summary.scalar("loss_obj", loss_obj)
with tf.name_scope("optimizer") as scope:
self.__train_step = tf.train.AdamOptimizer(1e-4).minimize(self.__loss)
# Merge op for tensorboard
self.__merged_summary_op = tf.summary.merge_all()
# Build graph
init = tf.global_variables_initializer()
# Saver for checkpoints
self.__saver = tf.train.Saver(max_to_keep=None)
# Avoid allocating the whole memory
gpu_options = tf.GPUOptions(per_process_gpu_memory_fraction=0.6)
self.__session = tf.Session(config=tf.ConfigProto(gpu_options=gpu_options))
# Configure summary to output at given directory
self.__writer = tf.summary.FileWriter("./logs/loc_logs", self.__session.graph)
self.__session.run(init)
定位的其他应用
使用 CNN 在图像中输出兴趣点坐标的想法可以扩展到许多其他应用。 其中一些包括人体姿势估计(《DeepPose:通过深度神经网络进行人体姿势估计》),如下所示:

为训练图像中的对象定义了关键点/地标。 对于所有训练图像中的特定对象,这些关键点位置必须一致。
例如,在面部关键点检测中,比如说我们有兴趣定位眼睛,鼻子和嘴巴,我们必须在所有训练面部图像的眼睛,鼻子和嘴巴周围定义多个关键点。 然后,就像前面的图像一样,我们训练 CNN 以输出预测的关键点位置,然后对这些输出关键点坐标应用回归损失以训练 CNN。 在测试时,将输入图像馈入 CNN 以预测所有关键点位置。 下图显示了面部关键点检测:

作为分类的对象检测 – 滑动窗口
对象检测与定位是一个不同的问题,因为我们可以在图像中包含数量可变的对象。 因此,如果我们将检测视为像定位一样简单的回归问题,处理可变数量的输出将变得非常棘手。 因此,我们将检测视为分类问题。
长期使用的一种非常常见的方法是使用滑动窗口进行对象检测。 想法是在输入图像上滑动固定大小的窗口。 然后,将窗口中每个位置的内容发送到分类器,该分类器将告诉我们该窗口是否包含感兴趣的对象。
为此,人们可以首先训练一个 CNN 分类器,其中包含我们想要检测的对象的小幅裁剪图像-调整大小与窗口大小相同。 汽车。 在测试时,固定大小的窗口会在要检测对象的整个图像中以滑动的方式移动。然后,我们的 CNN 会为每个窗口预测是否是一个对象(在这种情况下是汽车)。
仅使用一种尺寸的滑动窗口,我们只能检测一种尺寸的对象。 因此,要查找更大或更小的对象,我们还可以在测试时使用更大或更小的窗口,并在将其发送到分类器之前调整内容的大小。 或者,您可以调整整个输入图像的大小,并仅使用一个尺寸的滑动窗口,该窗口也将在这些调整大小的图像上运行。 两种方法都可以使用,但其想法是产生所谓的“比例尺金字塔”,以便我们可以检测图像中不同尺寸的对象。
这种方法的最大缺点是,各种比例的大量窗口可能会通过 CNN 进行预测。 这使得将 CNN 用作分类器在计算上非常昂贵。 同样对于大多数这些窗口,它们将始终不包含任何对象。
为了克服这个问题,已经进行了许多改进。 在以下各节中,我们将介绍为解决该问题而创建的各种技术和算法,以及较之以前的技术和算法如何进行了改进。
使用启发式技术指导我们(R-CNN)
为了避免在输入图像上每个可能的位置(大多数都不会包含对象)运行分类器,我们可以使用一些外部方法向我们建议可能的区域。 一种可以做到这一点的方法称为选择搜索。
区域提议方法将在图像中提供类似斑点的矩形区域,这些区域可能包含感兴趣的对象。 这些区域是存在感兴趣对象的候选区域。 然后,仅将 CNN 分类器应用于这些建议的区域。 与滑动窗口方法相比,这大大减少了发送到 CNN 进行分类的农作物的数量。
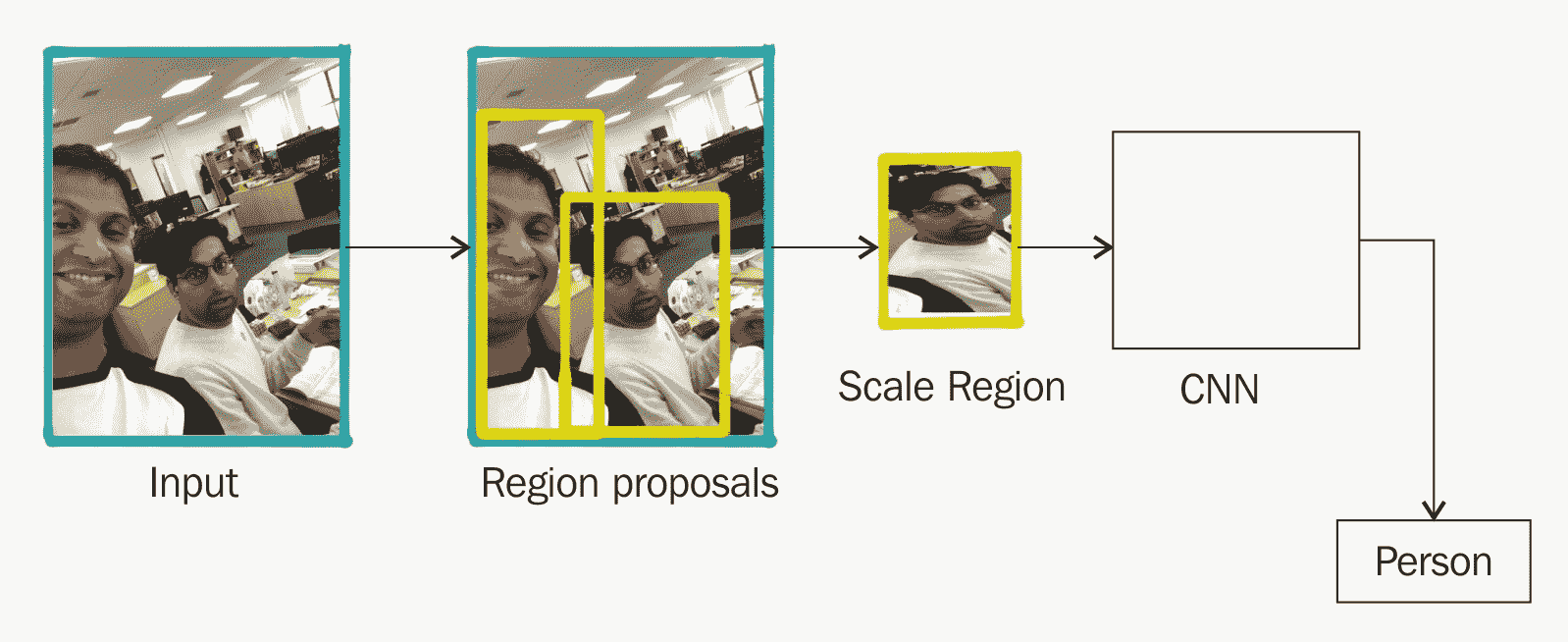
该特定方法在 2013 年提出,并被称为 R-CNN:区域 CNN。 下图描述了 R-CNN 的过程:
问题
R-CNN 在计算上仍然很昂贵,因为您必须对大约 2,000 个单独的区域候选运行 CNN。 结果,训练和测试都非常慢。 CNN 分类器依赖于通过选择性搜索进行检测而生成的固定数量的矩形候选窗口。 这种方法并不是最快的方法,而且由于无法从训练数据中了解候选区域,因此它们可能不是针对任务的最佳选择。
Fast R-CNN
2015 年,提出了快速 R-CNN 来解决 R-CNN 的速度问题。 在此方法中,主要的变化是我们在流水线中获取投标区域的位置。 首先,我们通过 CNN 运行整个输入图像,而不是从输入图像中直接获取它们,并提取靠近网络末端的生成的特征图。 接下来,再次使用区域提议方法,以与 R-CNN 类似的方式从该特征图中提取候选区域。
以这种方式获取建议有助于重用和共享昂贵的卷积计算。 网络中位于网络下方的全连接层将分类并另外定位,仅接受固定大小的输入。 因此,使用称为 RoI 池的新层将特征图中建议的区域扭曲为固定大小(在下一节中进一步讨论)。 RoI 池会将区域大小调整为最后一个 FC 层所需的大小。 下图显示了整个过程:
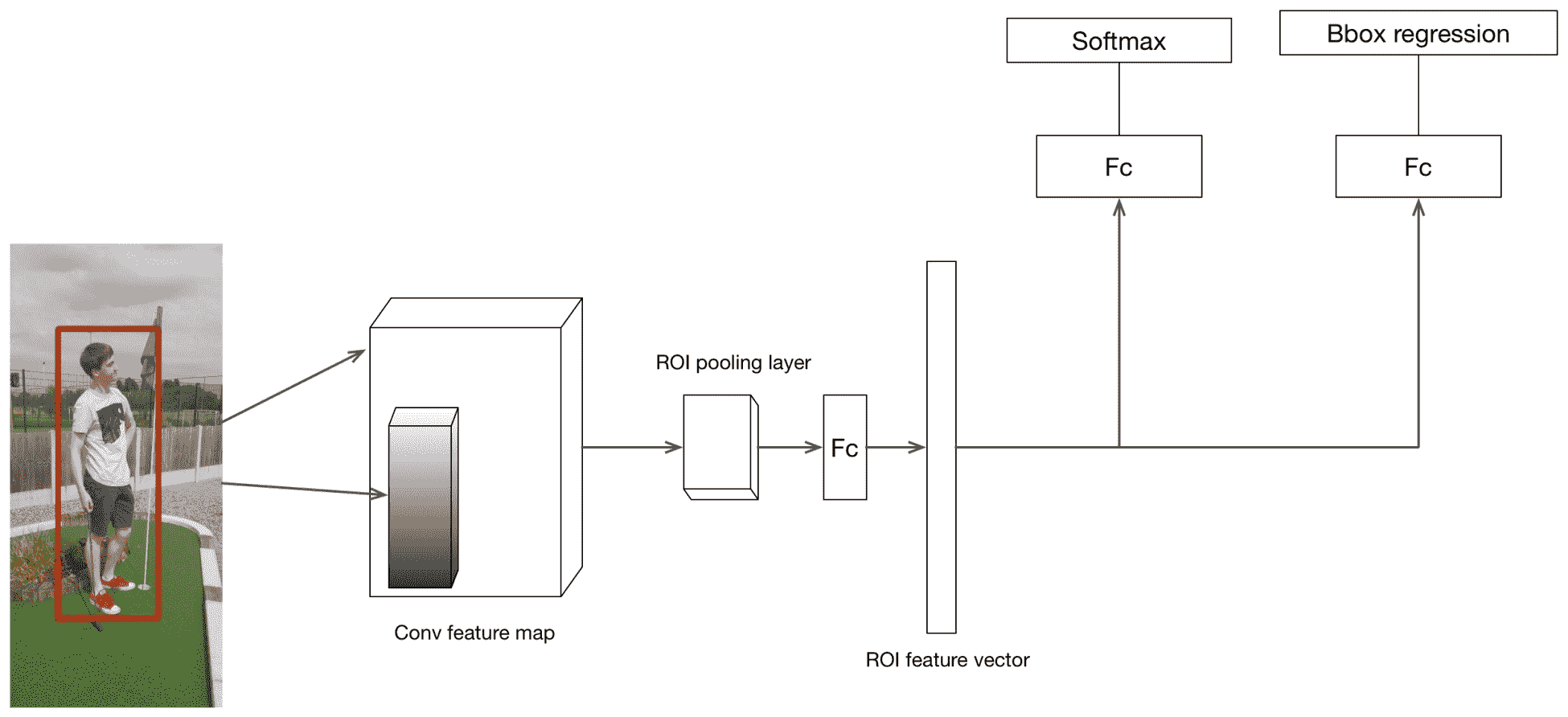
R-CNN 与 FastRCNN 的比较表明,后者在训练时快约 10 倍,而在测试时快约 150 倍(使用 VGG 架构作为主要 CNN 时)。
Faster R-CNN
这项技术在 2015 年 Fast R-CNN 之后不久提出,解决了使用外部区域建议方法的需求,并消除了与之相关的计算成本。
该算法的主要区别在于,不是使用外部算法(例如选择性搜索)来创建候选,而是使用称为区域候选网络(RPN)的子网为我们学习并提出建议。 在此屏幕快照中显示:

区域候选网
RPN 的工作是预测我们称为锚点的对象(本质上只是一个边界框)是否包含对象或仅是背景,然后完善此边界框的位置。
基本上,RPN 通过在最后一个 CNN 特征图上滑动一个小窗口(3 x 3)来做到这一点(同一特征图 Fast R-CNN 从中获得建议)。 对于每个滑动窗口中心,我们创建k固定锚框,并将这些框分类为是否包含对象:
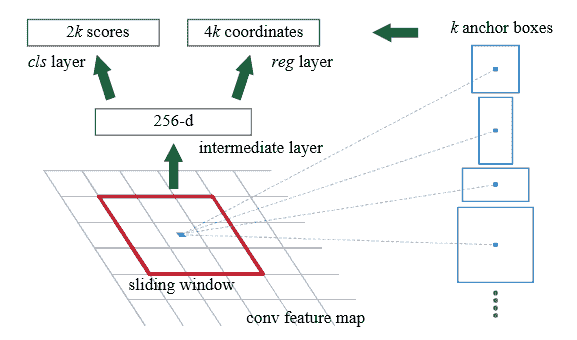
在内部,在训练过程中,我们选择 IoU 最大的锚定边界框和真实情况边界框进行反向传播。
RoI 池化层
RoI 池层只是最大池的一种,池的大小取决于输入的大小。 这样做可以确保输出始终具有相同的大小。 使用该层是因为全连接层始终期望输入大小相同,但是 FC 层的输入区域可能具有不同的大小。
RoI 层的输入将是建议和最后的卷积层激活。 例如,考虑以下输入图像及其建议:
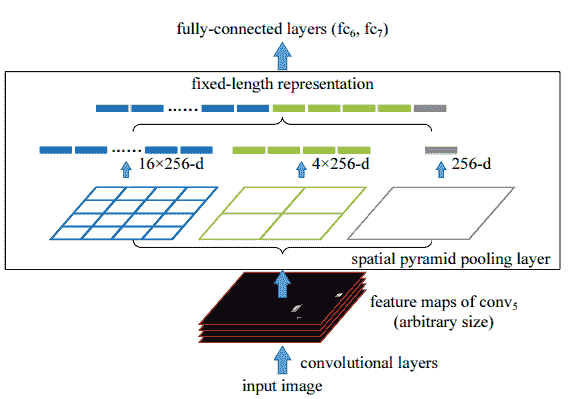
这里,我们有一个表格,总结了方法之间的差异:
| R-CNN | Fast R-CNN | Faster R-CNN | |
|---|---|---|---|
| 每个图像的测试时间 | 50 秒 | 2 秒 | 0.2 秒 |
| 加速 | 1 倍 | 25 倍 | 250 倍 |
| 准确率 | 66% | 66.9% | 66.9% |
将传统的 CNN 转换为全卷积网络
对于有效的对象检测器而言,非常重要的一点是提高卷积,从而提高计算的重用性。 为此,我们将所有 FC 层转换为卷积层,如下图所示。
以这种方式实现我们的网络的目的是,他们可以使用比其最初设计的图像更大的图像作为输入,同时共享计算以使其效率更高。 将所有 FC 层都转换为卷积层的这种类型的网络的名称称为完全卷积网络(FCN)。
将 FC 层转换为卷积层的基本技术是使用与输入空间尺寸一样大的内核大小,并使用过滤器数来匹配 FC 层上的输出数。 在此示例中,我们期望输入图像为14x14x3。
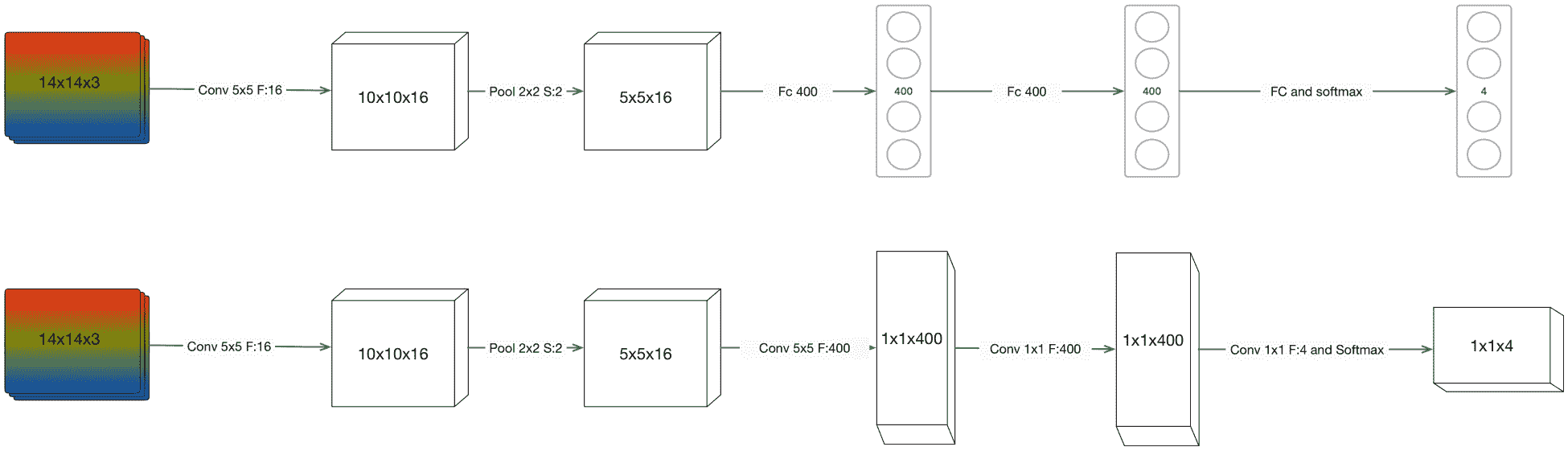
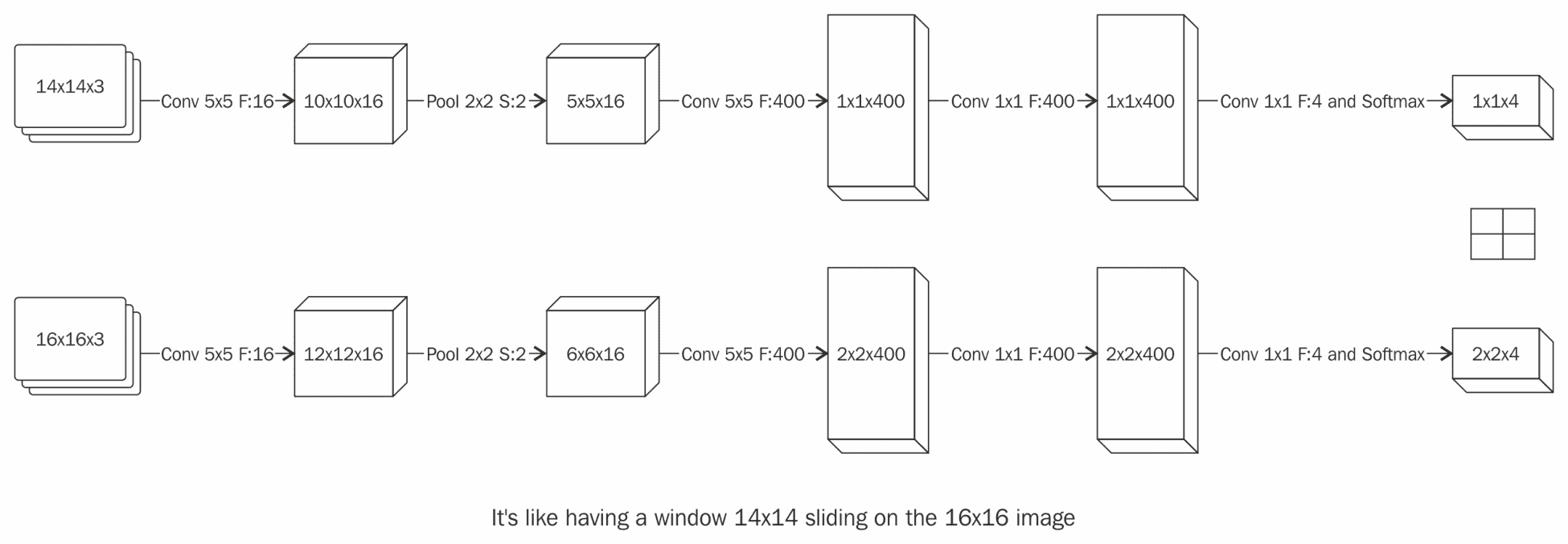
以我们为例,用100 x 100的输入补丁训练一个全卷积网络,并用2,000 x 2,000的输入图像进行测试,结果将是在2000 x 2000图像上运行100 x 100的滑动窗口 。 当使用较大的输入体积(如本例中所示)时,FCN 的输出将是一个体积,其中每个单元格对应于原始输入图像上100x100窗口补丁的一张幻灯片。
现在,每次我们使用比原始训练输入大的输入图像时,效果都将像我们实际上在整个图像上滑动分类器,但计算量却减少了。 通过这种方式,我们通过 CNN 的前向传递一步一步地使滑动窗口卷积:
单发检测器 – 您只看一次
在本节中,我们将继续介绍一种稍有不同的对象检测器,称为单发检测器。 单发检测器尝试将对象检测伪装为回归问题。 此类别下的主要架构之一是 YOLO 架构(您只看一次),我们现在将对其进行详细介绍。
YOLO 网络的主要思想是在不使用任何滑动窗口的情况下优化输入图像中各个位置的预测计算。为实现此目的,网络以大小为N x N单元格的网格形式输出特征图。
每个单元格都有B * 5 + C条目。 其中B是每个单元格的边界框的数量,C是类概率的数量,而 5 是每个边界框的元素(x, y:边界框相对于其所在单元格的中心点坐标, w是相对于原始图像的边界框的宽度, h是相对于原始图像的边界框的高度,置信度:边界框中对象存在的可能性)。
我们将置信度得分定义为:

如果单元格中没有对象,则将为零。 否则将等于真实情况框与预测框之间的 IOU。
请注意,网格的每个单元格都负责预测固定数量的边界框。
下图描述了作为 YOLO 网络输出的单元格条目的样子,它预测了形状的张量(N, N, B * 5 + C)。 网络的最后一个卷积层将输出与栅格尺寸相同大小的特征图。
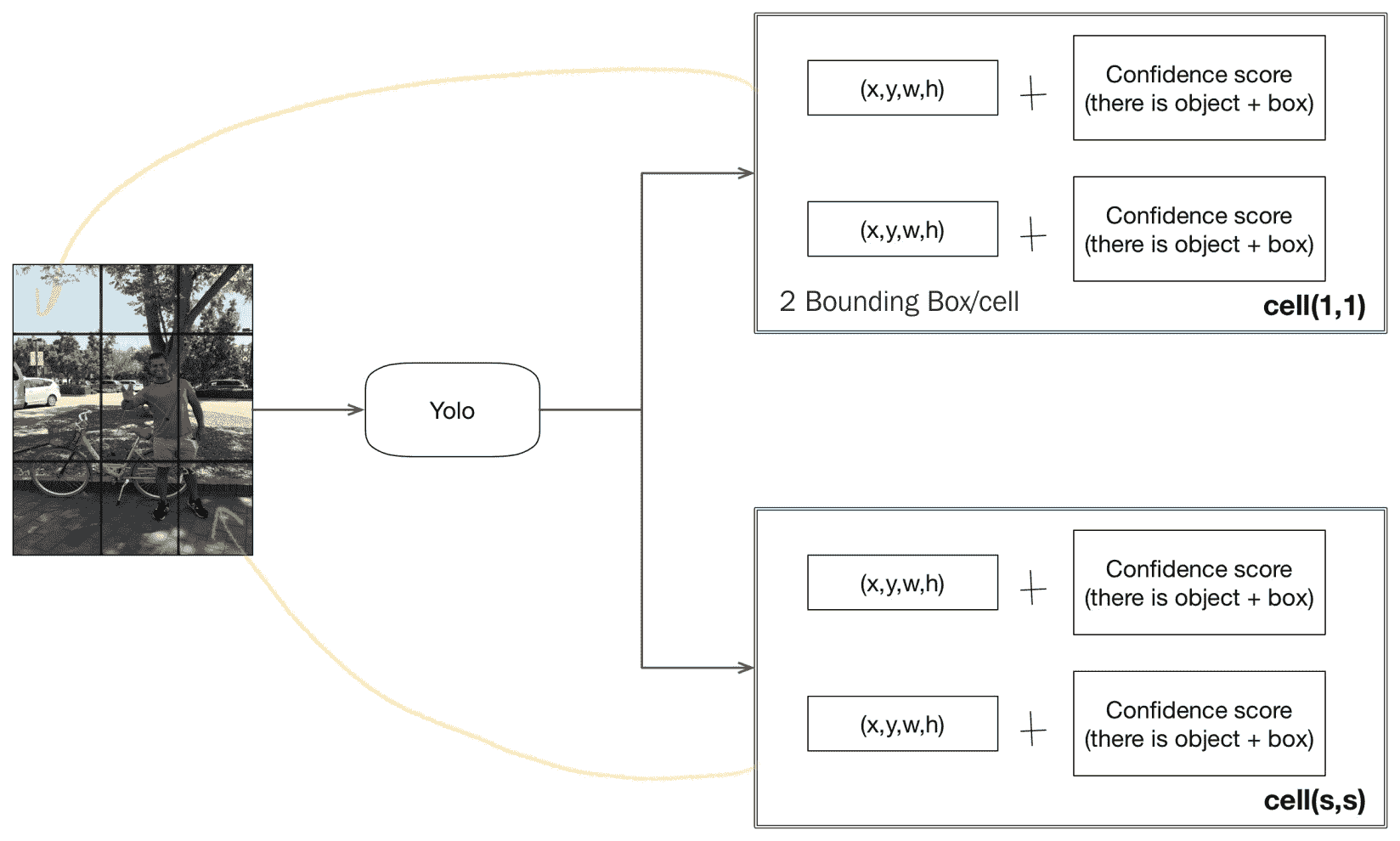
中心坐标以及边界框的高度和宽度在[0, 1]之间进行归一化。 下图显示了如何计算这些坐标的示例:
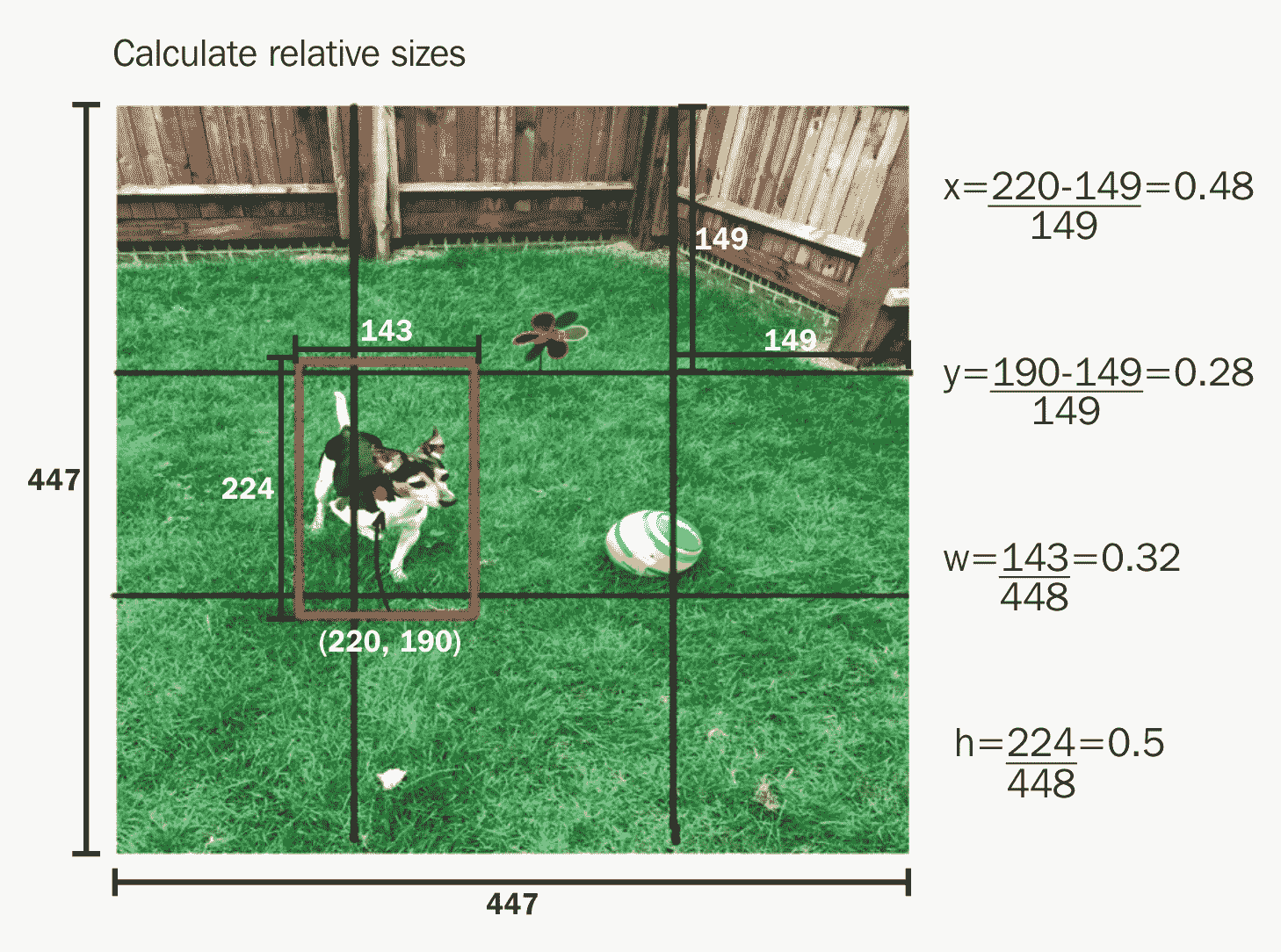
网络为每个单元格预测类别概率,边界框和这些框的置信度。
实际的 YOLO 网络具有 24 个卷积层,其后是 2 个全连接层。 但是,Fast YOLO 网络是 9 层,如下所示:

另一个重要的一点是,即使每个对象似乎位于多个像元上,也将单独将其分配给一个栅格像元(基于此中心和像元距离)。
目前,我们可以想象在图像上可以检测到的对象数量将是网格大小。 稍后,我们将看到如何处理每个网格单元的多个对象。 (锚盒)
创建用于 Yolo 对象检测的训练集
为了创建 YOLO 的训练集,将与 YOLO 网络的输出特征图预测相同大小的网格放置在每个训练输入图像上。 对于网格中的每个像元,我们创建一个目标向量Y,其长度为B * 5 + C(即与上一节中的输出特征图网格像元大小相同)。
让我们以训练图像为例,看看如何为图像上的网格中的单元创建目标向量:
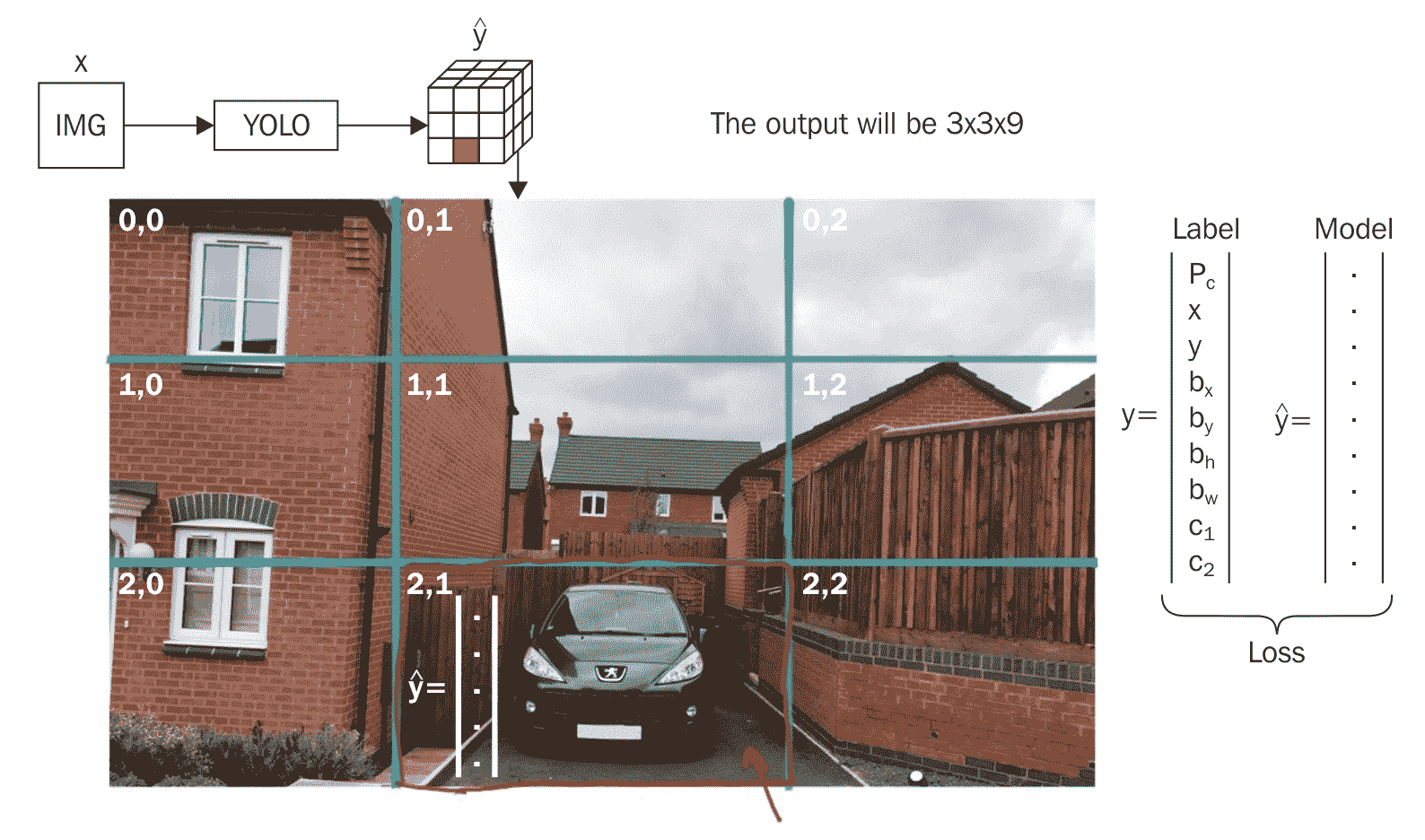
在上图中,考虑我们根据对象中心的最短距离来选择单元(在图像中,后车的中心最靠近绿色单元)。 如果我们看一下上面的训练图像,我们会注意到感兴趣的对象仅存在于一个单元格编号为 8 的单元格中。其余的单元格 1-7 和 9 没有任何感兴趣的对象。 每个单元的目标向量将具有 16 个条目,如下所示:
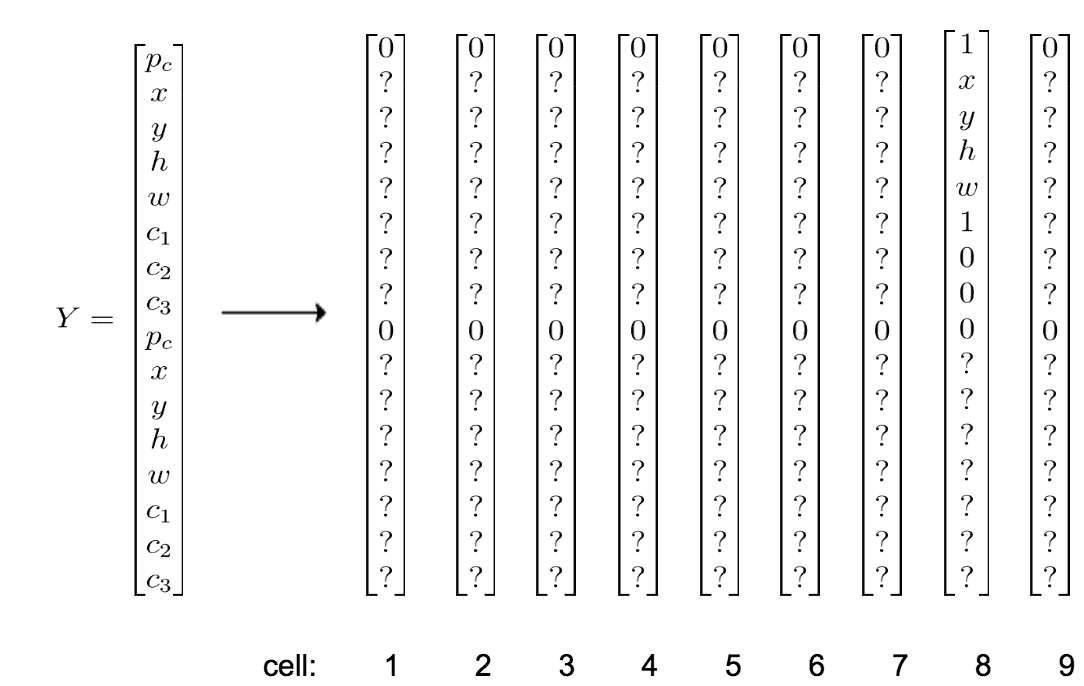
第一个条目是类别P[c]存在的置信度得分,对于没有对象的单元格中的两个锚定框,该得分均为 0。 其余值将无关。 单元格编号 8 有一个对象,并且对象的边界框具有较高的 IOU。
对于大小为NxM的输入训练图像,训练后从卷积网络输出的目标向量的最终体积将为3x3x16(在此玩具示例中)
数据集中每个图像的标签信息将仅包括对象的中心坐标及其边界框。 实现代码以使其与网络的输出向量相匹配是您的责任; 这些任务包括以下所列的任务:
- 将每个中心点的图像空间转换为网格空间
- 将图像空间上的边界框尺寸转换为网格空间尺寸
- 查找图像空间上最接近对象的单元格
如果我们将每个单元格类别的概率乘以每个边界框的置信度,我们将获得一些可以用另一种算法(非最大值抑制)过滤的检测结果。
让我们将置信度定义为反映单元格上任何类对象是否存在的事物。 (请注意,如果单元格上没有对象,则置信度应为零,如果有对象,则置信度应为 IoU):
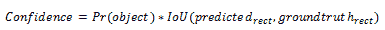
我们还需要定义一个条件类别概率; 给定对象P(class | Pr)的存在,我们想要这样做是因为我们不希望损失函数在单元格上没有对象的情况下惩罚错误的类预测。 该网络仅预测每个单元格的一组类别概率,而不考虑框数B。
评估检测(交并比)
在继续进行之前,我们需要知道如何衡量我们的模型是否正确检测到对象。 为此,我们计算会返回一个数字的交并比(IoU),根据某个参考(真实情况)告诉我们检测的效果如何。 IoU 的计算方法是:将检测和地面真理框彼此重叠的区域除以检测和地面真理框所覆盖的总面积:
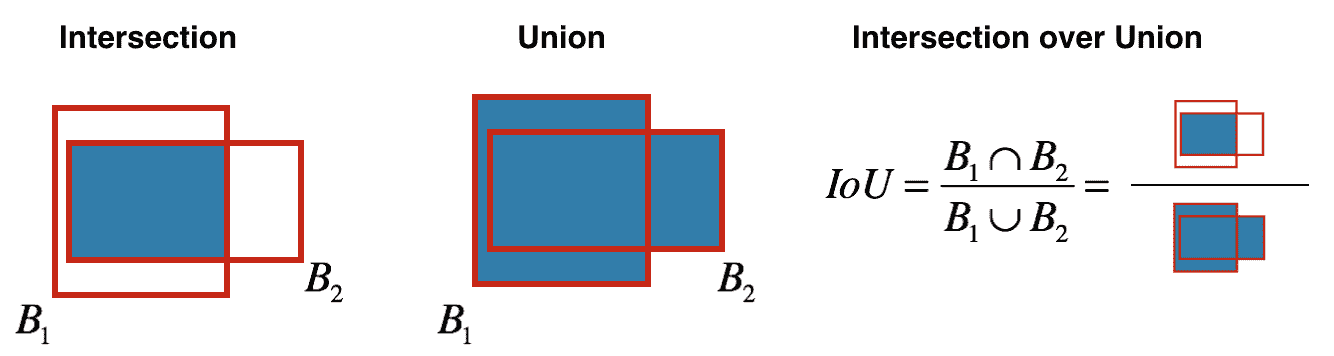
这是一个糟糕,良好和出色的 IoU 的示例:
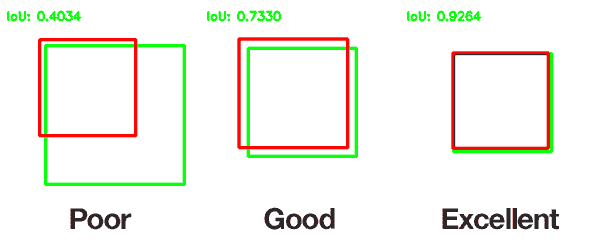
按照惯例,如果 IoU 大于 0.5,我们认为这两个方框都匹配,并且在这种情况下,检测为真阳性。
IoU 为零表示框不相交,IoU 为 1 表示完美匹配。
在我们的检测器上,如果一个单元有多个锚定框,则 IoU 会帮助选择哪个对目标负责。我们选择具有最高实测值的 IoU 最高的锚定。
这是 IoU 的 Python 代码:
def iou_non_vectorized(box1, box2):
# If one of the rects are empty return 0 (No intersect)
if box1 == [] or box2 == []:
return 0
# size of intersect divided by size of union of 2 rects
# Get rectangle areas format (left,top,right,bottom)
box_1_area = (box1[2] - box1[0] + 1) * (box1[3] - box1[1] + 1)
box_2_area = (box2[2] - box2[0] + 1) * (box2[3] - box2[1] + 1)
# Get the intersection coordinates (x1,y1,x2,y2)
intersect_x1 = max(box1[0], box2[0])
intersect_y1 = max(box1[1], box2[1])
intersect_x2 = min(box1[2], box2[2])
intersect_y2 = min(box1[3], box2[3])
# Calculate intersection area
intersect_area = (intersect_x2 - intersect_x1 + 1) * (intersect_y2 - intersect_y1
+ 1)
return intersect_area / float(box_1_area + box_2_area - intersect_area)
We can also change this to a vectorized form on Tensorflow
def tf_iou_vectorized(self, box_vec_1, box_vec_2):
def run(tb1, tb2):
# Break the boxes rects vector in sub-vectors
b1_x1, b1_y1, b1_x2, b1_y2 = tf.split(box_vec_1, 4, axis=1)
b2_x1, b2_y1, b2_x2, b2_y2 = tf.split(box_vec_2, 4, axis=1)
# Get rectangle areas format (left,top,right,bottom)
box_vec_1_area = (b1_x2 - b1_x1 + 1) * (b1_y2 - b1_y1 + 1)
box_vec_2_area = (b2_x2 - b2_x1 + 1) * (b2_y2 - b2_y1 + 1)
xA = tf.maximum(b1_x1, tf.transpose(b2_x1))
yA = tf.maximum(b1_y1, tf.transpose(b2_y1))
xB = tf.minimum(b1_x2, tf.transpose(b2_x2))
yB = tf.minimum(b1_y2, tf.transpose(b2_y2))
interArea = tf.maximum((xB - xA + 1), 0) * tf.maximum((yB - yA + 1), 0)
iou = interArea / (box_vec_1_area + tf.transpose(box_vec_2_area) - interArea)
return iou
op = run(self.tf_bboxes1, self. tf_bboxes2)
self.sess.run(op, feed_dict={self.tf_bboxes1: box_vec_1, self.tf_bboxes2: box_vec_2})
tic = time()
self.sess.run(op, feed_dict={self.tf_bboxes1: box_vec_1, self.tf_bboxes2: box_vec_2})
toc = time()
return toc - tic
我们也可以在 TensorFlow 上将其更改为向量化形式,如下所示:
def tf_iou_vectorized(self, box_vec_1, box_vec_2):
def run(tb1, tb2):
# Break the boxes rects vector in sub-vectors
b1_x1, b1_y1, b1_x2, b1_y2 = tf.split(box_vec_1, 4, axis=1)
b2_x1, b2_y1, b2_x2, b2_y2 = tf.split(box_vec_2, 4, axis=1)
# Get rectangle areas format (left,top,right,bottom)
box_vec_1_area = (b1_x2 - b1_x1 + 1) * (b1_y2 - b1_y1 + 1)
box_vec_2_area = (b2_x2 - b2_x1 + 1) * (b2_y2 - b2_y1 + 1)
xA = tf.maximum(b1_x1, tf.transpose(b2_x1))
yA = tf.maximum(b1_y1, tf.transpose(b2_y1))
xB = tf.minimum(b1_x2, tf.transpose(b2_x2))
yB = tf.minimum(b1_y2, tf.transpose(b2_y2))
interArea = tf.maximum((xB - xA + 1), 0) * tf.maximum((yB - yA + 1), 0)
iou = interArea / (box_vec_1_area + tf.transpose(box_vec_2_area) - interArea)
return iou
op = run(self.tf_bboxes1, self. tf_bboxes2)
self.sess.run(op, feed_dict={self.tf_bboxes1: box_vec_1, self.tf_bboxes2: box_vec_2})
tic = time()
self.sess.run(op, feed_dict={self.tf_bboxes1: box_vec_1, self.tf_bboxes2: box_vec_2})
toc = time()
return toc - tic
过滤输出
实际上,您的模型通常会返回同一对象的多个检测窗口。 为了解决这个问题,我们使用一种称为非最大抑制的算法。 该算法使用“IoU 和对象的存在”作为启发式过滤这些多个框。 运作方式如下:
- 丢弃所有包含对象的可能性低的框(
pc < 0.6) - 选择最有可能出现对象的盒子(标签上的
pc) - 丢弃与所选框高度重叠的所有框(
IoU > 0.5) - 重复步骤 2 和 3,直到所有检测都被放弃或选择为止
我们将在检测器的预测时间上使用非最大抑制:
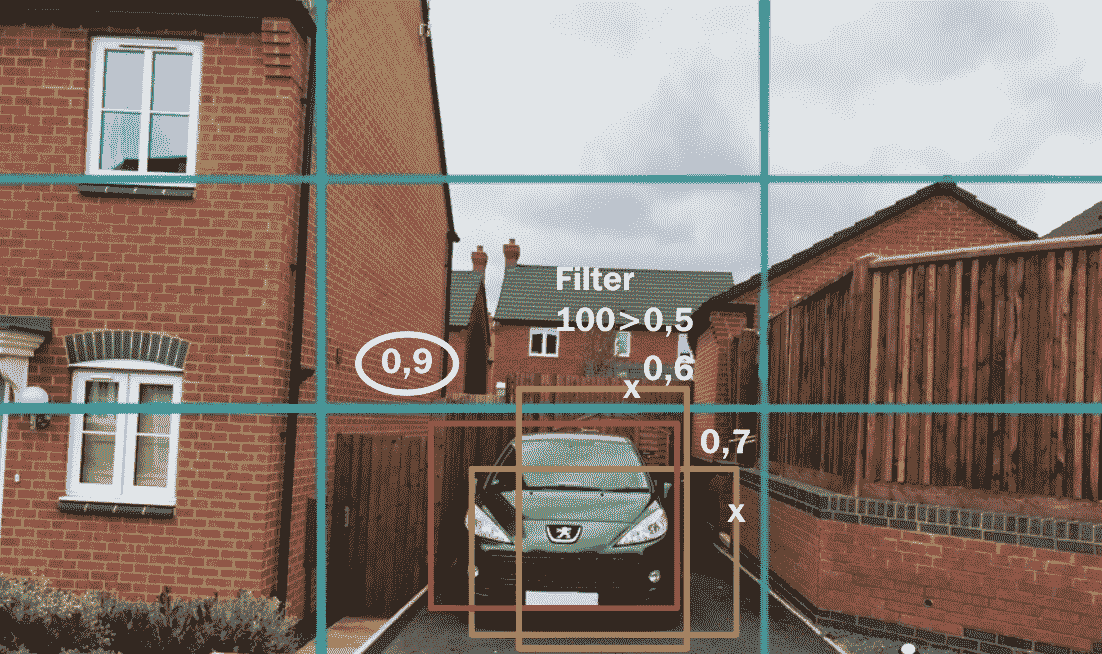
Tensorflow 已经具有实现非最大值抑制算法的功能,称为tf.image.non_max_suppression。
锚框
锚框预定义的模板框,具有一定的高宽比。 这些在 YOLO 中用于帮助检测单个网格单元中的多个对象。 我们根据可以检测到的对象类型的大致几何形状定义盒子的形状。
目前,正如所解释的,我们的模型将只能在每个网格单元中检测到一个对象,但是在大多数情况下,每个网格中可能有多个对象。 请记住,我们认为最靠近对象的像元是中心:
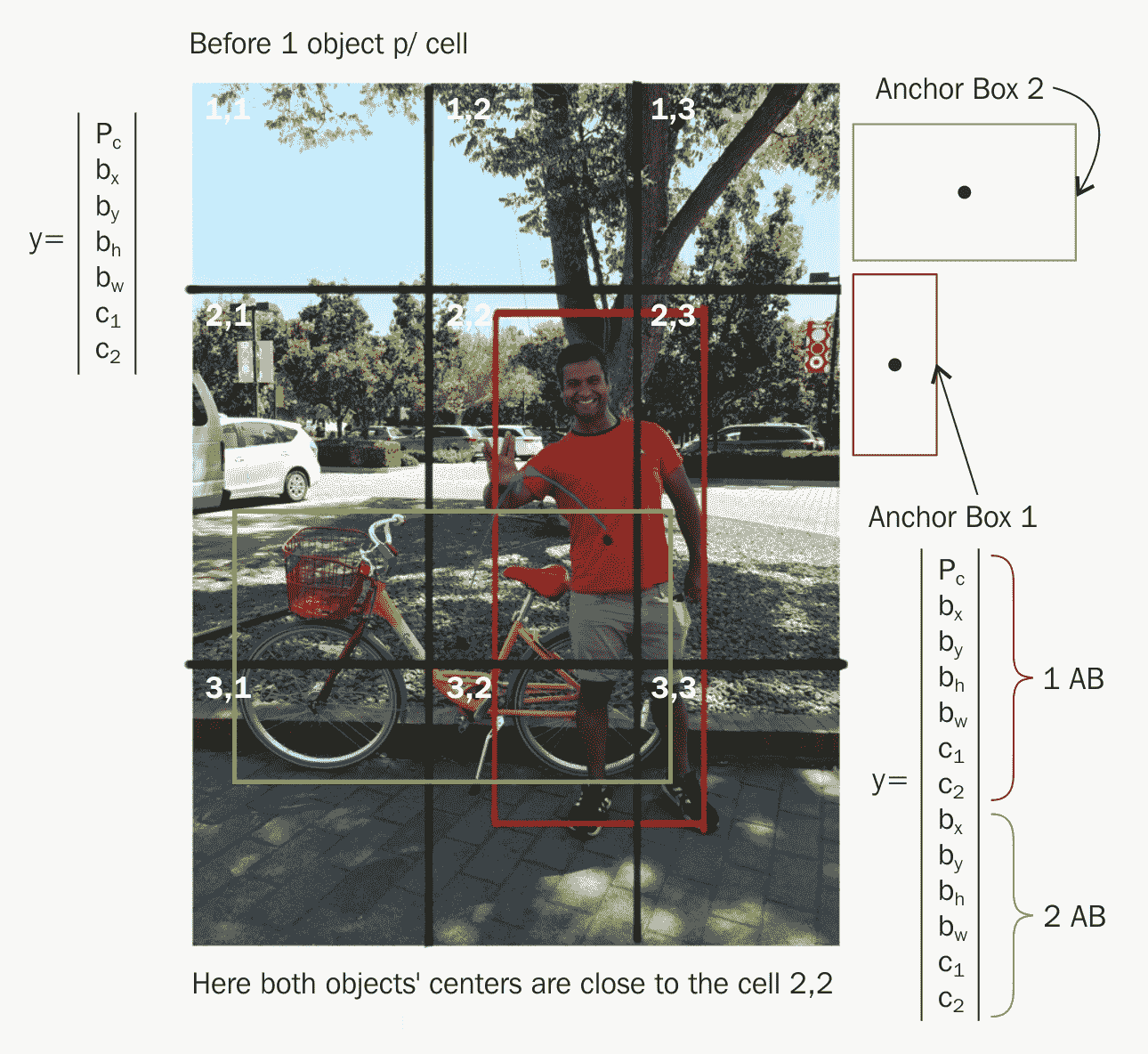
为了解决这个问题,我们需要锚点。 基本上,我们将在输出深度体积中添加预定义的边界框; 然后,在训练过程中,我们选择中心最接近特定单元格的对象,并选择与锚框具有最大 IoU 的边界框。 实际上,由于多个子网将负责在同一单元中查找其他对象,因此,锚定框的想法使网络更好地概括了检测范围。
在 Yolo 中进行测试/预测
现在将先前汽车图像中的图像视为我们的测试图像。 每个像元的预测向量的输出为:

请注意,...条目表示即使对于没有对象的单元格,预测向量中也会有一些随机值。 但是,在单元格 8 中,x, y, h, w的预测值有望接近准确。
在最后阶段,我们可以使用非最大值抑制算法过滤每个像元中的多个预测边界框。
检测器损失函数(YOLO 损失)
作为定位器,YOLO 损失函数分为三个部分:负责查找边界框坐标,边界框分数预测和类分数预测的部分。 它们都是均方误差损失,并由预测和真实情况情况之间的一些标量元参数或 IoU 得分进行调制:

成员1[ij]^obj成员用于基于特定单元i, j上对象的存在来调制损失:
- 如果在网格单元格
i和第j个边界框中具有最高 IoU 的对象存在:1 - 否则:0
同样,1[ij]^noobj正好相反。
损失第 1 部分

第一部分计算与预测的边界框位置坐标(x, y)相关的损失。 (x_hat, y_hat)是训练集中真实情况数据的边界框坐标。
λ[coord] = 5.0表示一个常数,当有错误时,该常数将给予更多的补偿。 B是边界框的数量。 S^2是网格中的单元数。
使用类似的公式来处理边界框的宽度/高度

损失函数方程中宽度和高度的平方根用来反映小盒子中的小偏差比大盒子中的重要。 一般而言,这部分损失会对边界框的高度和宽度不正确进行惩罚。
损失第 2 部分
损失函数的这一部分计算与每个边界框预测变量的置信度得分相关的损失。

C是置信度分数(受对象的存在调制的项)。C_hat是带有真实情况的预测边界框的 IOU。 参数λ[noobj] = 0.5用于使无对象时的损失关注度降低。
损失第 3 部分
分类损失是损失函数的最后一部分。

该损失是分类误差损失平方的总和。 同样,当单元上有一个对象时,项1[i]^(obj)为 1,否则为 0。 我们的想法是,当存在对象时,我们不考虑分类错误。
1[i]^(obj), 1[ij]^(obj), 1[ij]^(noobj)这些项可以掩盖我们在真实情况上有一个对象而在特定单元的模型输出中有一个对象的情况下的损失。 当真实情况与模型输出不匹配时,也是如此。
因此,例如,当特定单元格不匹配时,我们的损失将是:

当我们有比赛时:
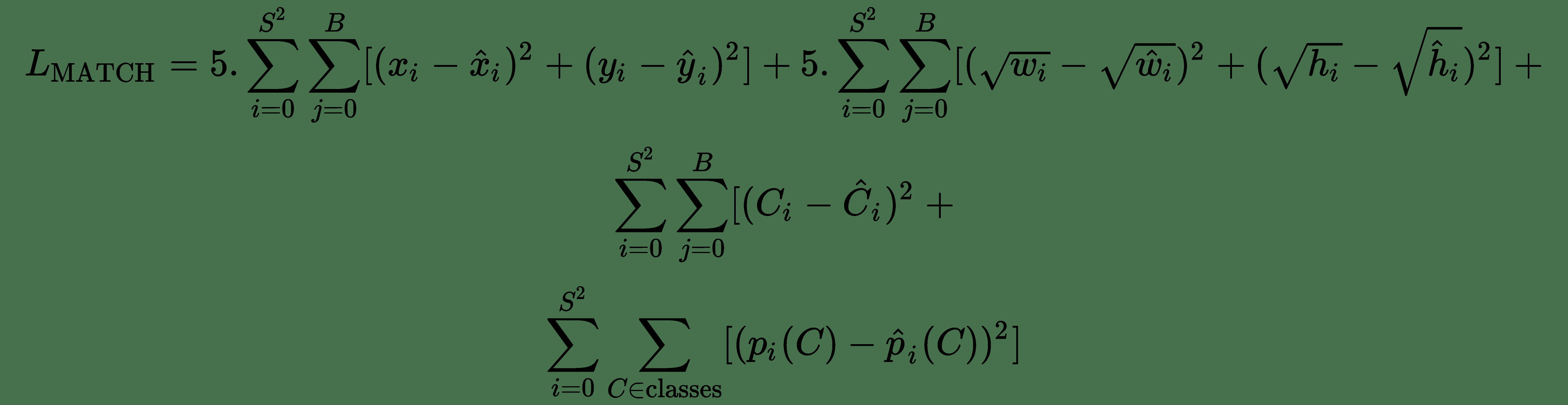
在实践中的实践中,您将尝试向量化这种损失并避免for循环并提高性能,这对于 Tensorflow 之类的库尤其如此。
这是 YOLO 损失的 TensorFlow 实现:
def loss_layer(self, predicts, labels, scope='loss_layer'):
with tf.variable_scope(scope):
predict_classes = tf.reshape(predicts[:, :self.boundary1], [self.batch_size, self.cell_size, self.cell_size, self.num_class])
predict_scales = tf.reshape(predicts[:, self.boundary1:self.boundary2], [self.batch_size, self.cell_size, self.cell_size, self.boxes_per_cell])
predict_boxes = tf.reshape(predicts[:, self.boundary2:], [self.batch_size, self.cell_size, self.cell_size, self.boxes_per_cell, 4])
response = tf.reshape(labels[:, :, :, 0], [self.batch_size, self.cell_size, self.cell_size, 1])
boxes = tf.reshape(labels[:, :, :, 1:5], [self.batch_size, self.cell_size, self.cell_size, 1, 4])
boxes = tf.tile(boxes, [1, 1, 1, self.boxes_per_cell, 1]) / self.image_size
classes = labels[:, :, :, 5:]
offset = tf.constant(self.offset, dtype=tf.float32)
offset = tf.reshape(offset, [1, self.cell_size, self.cell_size, self.boxes_per_cell])
offset = tf.tile(offset, [self.batch_size, 1, 1, 1])
predict_boxes_tran = tf.stack([(predict_boxes[:, :, :, :, 0] + offset) / self.cell_size,
(predict_boxes[:, :, :, :, 1] + tf.transpose(offset,
(0, 2, 1, 3))) / self.cell_size,
tf.square(predict_boxes[:, :, :, :, 2]),
tf.square(predict_boxes[:, :, :, :, 3])])
predict_boxes_tran = tf.transpose(predict_boxes_tran, [1, 2, 3, 4, 0])
iou_predict_truth = self.tf_iou_vectorized(predict_boxes_tran, boxes)
# calculate I tensor [BATCH_SIZE, CELL_SIZE, CELL_SIZE, BOXES_PER_CELL]
object_mask = tf.reduce_max(iou_predict_truth, 3, keep_dims=True)
object_mask = tf.cast((iou_predict_truth >= object_mask), tf.float32) * response
# calculate no_I tensor [CELL_SIZE, CELL_SIZE, BOXES_PER_CELL]
noobject_mask = tf.ones_like(object_mask, dtype=tf.float32) - object_mask
boxes_tran = tf.stack([boxes[:, :, :, :, 0] * self.cell_size - offset,
boxes[:, :, :, :, 1] * self.cell_size - tf.transpose(offset, (0, 2, 1, 3)),
tf.sqrt(boxes[:, :, :, :, 2]),
tf.sqrt(boxes[:, :, :, :, 3])])
boxes_tran = tf.transpose(boxes_tran, [1, 2, 3, 4, 0])
# class_loss
class_delta = response * (predict_classes - classes)
class_loss = tf.reduce_mean(tf.reduce_sum(tf.square(class_delta), axis=[1, 2, 3]), name='class_loss') * self.class_scale
# object_loss
object_delta = object_mask * (predict_scales - iou_predict_truth)
object_loss = tf.reduce_mean(tf.reduce_sum(tf.square(object_delta), axis=[1, 2, 3]), name='object_loss') * self.object_scale
# noobject_loss
noobject_delta = noobject_mask * predict_scales
noobject_loss = tf.reduce_mean(tf.reduce_sum(tf.square(noobject_delta), axis=[1, 2, 3]), name='noobject_loss') * self.noobject_scale
# coord_loss
coord_mask = tf.expand_dims(object_mask, 4)
boxes_delta = coord_mask * (predict_boxes - boxes_tran)
coord_loss = tf.reduce_mean(tf.reduce_sum(tf.square(boxes_delta), axis=[1, 2, 3, 4]), name='coord_loss') * self.coord_scale
语义分割
在语义分割中,目标是根据像素所属的对象类别标记图像的每个像素。 最终结果是一个位图,其中每个像素将属于某个类:

有几种流行的 CNN 架构已被证明在分割任务中表现出色。 它们中的大多数是称为自编码器的一类模型的变体,我们将在第 6 章,“自编码器,变分自编码器和生成模型”中详细介绍。 现在,他们的基本思想是首先在空间上将输入量减小为某种压缩形式,然后恢复原始的空间大小:
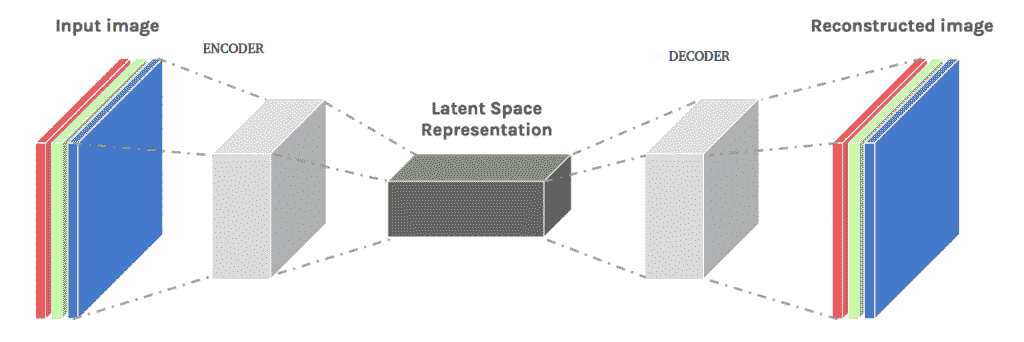
为了增加空间大小,使用了一些常用的操作,其中包括:
- 最大分割
- 反卷积/转置卷积
- 扩张/带孔卷积
我们还将学习语义分割任务中使用的 softmax 的新变体,称为空间 softmax 。
在本节中,我们将学习两个流行的模型,它们在语义分割上表现良好,并且具有非常简单的架构可供理解。 它们如下所示:
- FCN(全卷积网络)
- Segnet
需要解决的其他一些实现细节是:
- 最终的上采样层(Deconv)需要具有与分类一样多的过滤器,并且您的标签“颜色”需要与最后一层中的索引匹配,否则在训练过程中可能会遇到 NaN 问题
- 我们需要一个 Argmax 层来选择输出张量上概率最大的像素(仅在预测时间内)
- 我们的损失需要考虑输出张量上的所有像素
最大分割
取消池操作用于恢复最大池操作的效果。 这个想法只是充当上采样器。 此操作已在一些较早的论文上使用,并且不再使用,因为您还需要卷积层来修补(低通过滤器)上采样的结果:
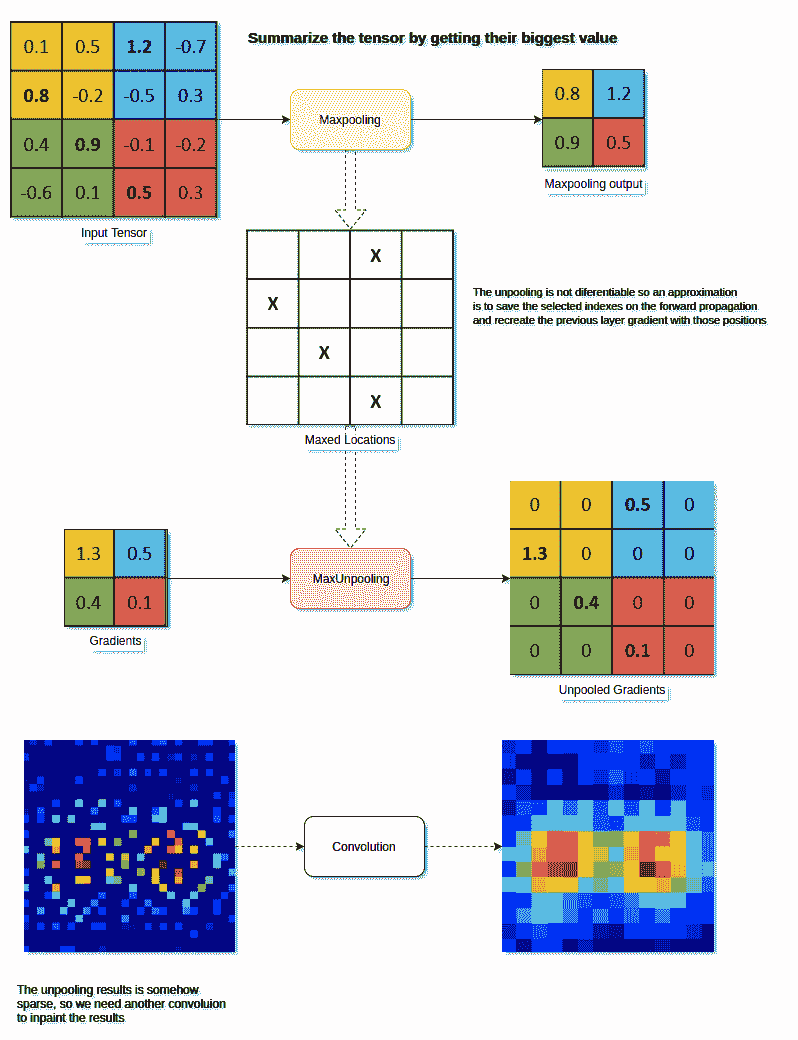
反卷积层(转置卷积)
这个运算相当不好地称为反卷积,这意味着它是卷积的逆运算,但实际上并非如此。 更恰当的名称是转置卷积或分数步卷积。
此层类型为您提供了一种对输入体积进行升采样的学习方法,并且可以在每次需要将输入特征图智能地投影到更高的空间时使用。 一些用例包括以下内容:
- 上采样(条纹转置卷积)
== UNPOOL + CONV - 可视化显着图
- 作为自编码器的一部分

在 Tensorflow 中,我们可以访问tf.layers中的转置卷积。 下面的示例将采用一个空间大小为14 x 14的输入,并使其通过conv2d_transpose层,其中输出空间大小为28 x 28:
# input_im has spatial dimensions 14x14 in this example
output = tf.layers.conv2d_transpose(inputs=input_im, filters=1, kernel_size=4, strides=2, padding='same')
选择kernel_size,步幅和填充方案时必须小心,因为它们都会影响输出空间大小。
损失函数
如前所述,分割模型的损失函数基本上是分类损失的扩展,但在整个输出向量中在空间上起作用:
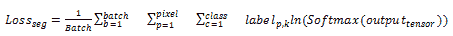
# Segmentation problems often uses this "spatial" softmax (Basically we want to classify each pixel)
with tf.name_scope("SPATIAL_SOFTMAX"):
loss = tf.reduce_mean((tf.nn.sparse_softmax_cross_entropy_with_logits(
logits=model_out,labels=tf.squeeze(labels_in, squeeze_dims=[3]),name="spatial_softmax")))
下图描述了用于语义分割的完全卷积网络的实现:
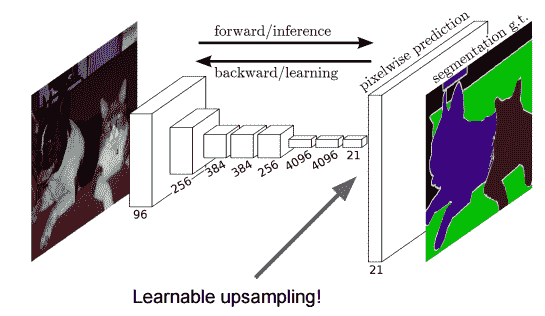
下图显示了 SegNet 架构:
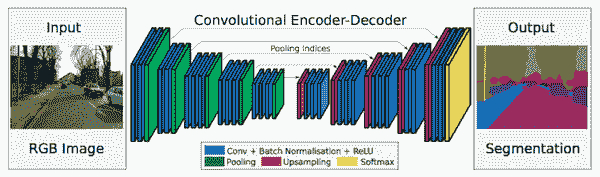
标签
如前所述,分割问题中的标签是一维图像,每个像素处的值与输出体积深度的索引匹配:

改善结果
通常,一种用于改善分割输出结果的技术是在后期处理阶段使用条件随机场(CRF),其中要考虑图像的纯 RGB 特征和我们的网络所产生的概率:
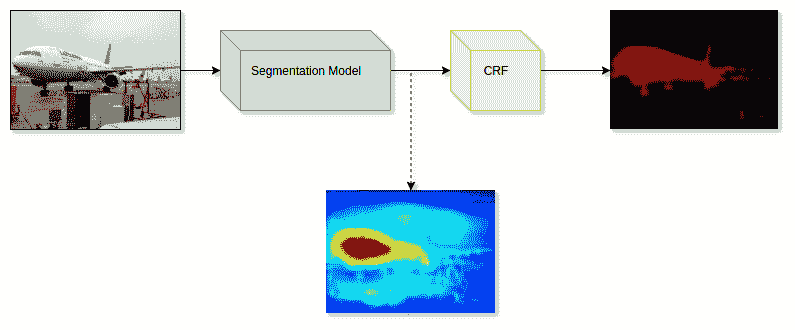
实例分割
实例分割是我们在本章中要讨论的最后一件事。 在许多方面,可以将其视为对象检测和语义分段的融合。 但是,与这两个问题相比,这绝对是难度增加。
通过实例分割,其思想是找到图像中一个或多个所需对象的每次出现,即所谓的实例。 找到这些实例后,即使它们属于同一类对象,我们也希望将它们彼此分开。 换句话说,标签既是类别感知的(例如汽车,标志或人),又是实例感知的(例如汽车 1,汽车 2 或汽车 3)。
实例分割的结果将如下所示:

这与语义分割之间的相似性很明显; 我们仍然根据像素所属的对象来标记像素。 但是,尽管语义分割不知道某个对象在图像实例中出现了多少次,但是分割却知道。
这种知道图像中有多少个对象实例的能力也使该问题类似于对象检测。 但是,对象检测产生的对象边界要粗糙得多,这意味着被遮挡的对象更容易被遗漏,实例分割不会发生这种情况。
Mask R-CNN
Mask R-CNN 是一种最近的网络架构,通过提供简单,灵活的模型架构可以使此问题更易于解决。 该架构于 2017 年发布,旨在扩展更快的 R-CNN 的功能:
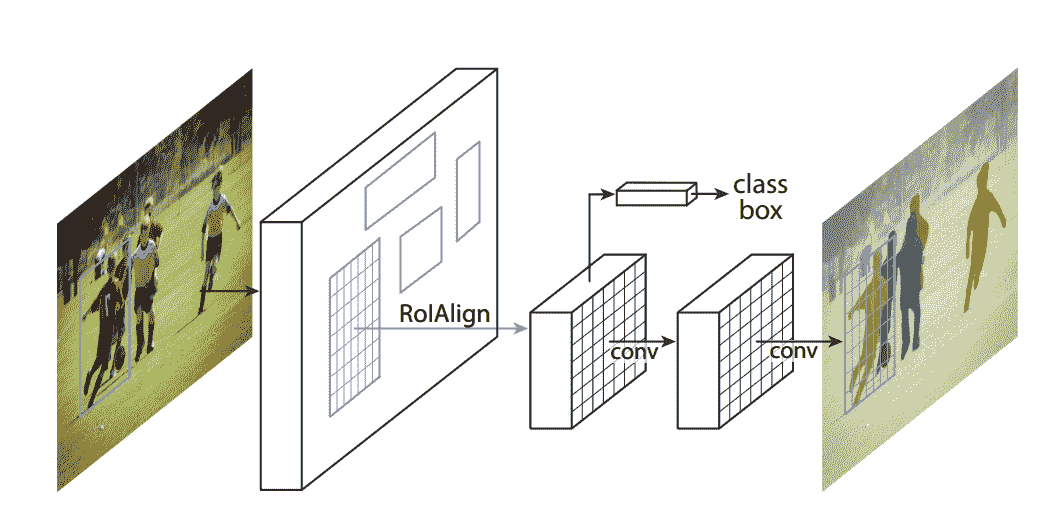
它采用现有的更快的 R-CNN 模型,并尝试通过向模型中添加一个分支来解决实例分割问题,该分支负责预测与分类和边界框回归头平行的对象蒙版。 在发布时,该架构被证明是有效的,并且在所有 COCO 挑战中均获得了最高荣誉。
总结
在本章中,我们学习了对象定位,检测和分段的基础知识。 我们还讨论了与这些主题相关的最著名的算法。
在下一章中,我们将讨论一些常见的网络架构。
五、VGG,Inception,ResNet 和 MobileNets
到目前为止,我们已经讨论了所有必要的构建块,以便能够实现常见问题(例如图像分类和检测)的解决方案。 在本章中,我们将讨论一些通用模型架构的实现,这些架构在许多常见任务中都表现出了很高的表现。 自从最初创建以来,这些架构一直很流行,并且在今天继续被广泛使用。
在本章的最后,您将对现有的不同类型的 CNN 模型及其在各种不同的计算机视觉问题中的用例进行了解。 在实现这些模型时,您将学习如何设计这些模型以及它们各自的优点。 最后,我们将讨论如何修改这些架构,以使训练和表现/效率更好。
总之,本章将涵盖以下主题:
- 如何提高参数效率
- 如何在 TensorFlow 中实现 VGG 网络
- 如何在 TensorFlow 中实现 Inception 网络
- 如何在 TensorFlow 中实现残差网络
- 如何实现对移动设备更友好的架构
替代大卷积
在开始之前,我们将首先学习可以减少模型使用的参数数量的技术。 首先,这很重要,因为它可以提高网络的泛化能力,因为使用该模型中存在的参数数量将需要较少的训练数据。 其次,较少的参数意味着更高的硬件效率,因为将需要更少的内存。
在这里,我们将从解释减少模型参数的重要技术入手,将几个小卷积级联在一起。 在下图中,我们有两个3x3卷积层。 如果回头看图右侧的第二层,可以看到第二层中的一个神经元具有3x3的感受域:

当我们说“感受域”时,是指它可以从上一层看到的区域。 在此示例中,需要一个3x3区域来创建一个输出,因此需要一个3x3的感受域。
回溯到另一层,该3x3区域的每个元素在输入端也具有3x3感受域。 因此,如果我们将所有这 9 个元素的接受场组合在一起,那么我们可以看到在输入上创建的总接受场大小为5x5。
因此,用简单的话来说,将较小的卷积级联在一起可以获得与使用较大卷积相同的感受域。 这意味着我们可以用级联的小卷积代替大卷积。
请注意,由于第一卷积层和输入文件深度之间的深度不匹配(输出的深度需要保持一致),因此无法在作用于输入图像的第一个卷积层上进行此替换:还应在图像上观察我们如何计算每层参数的数量。

在上图中,我们用三个3x3卷积替换了一个7x7卷积。 让我们自己计算一下,以减少使用的参数。
想象一下,在形状为WxHxC的输入体积上使用C过滤器进行7x7大小的卷积。 我们可以计算过滤器中的权数,如下所示:
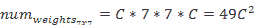
现在,相反,如果我们层叠三个3x3卷积(代之以7x7卷积),我们可以如下计算其权重数:
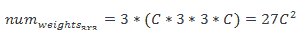
在这里,我们可以看到参数比以前更少!
还要注意,在这三个卷积层的每一个之间,我们放置了 ReLu 激活。 与仅使用单个大卷积层相比,这样做会给模型带来更多的非线性。 增加的深度(和非线性)是一件好事,因为这意味着网络可以将更多的概念组合在一起,并提高其学习能力!
大多数新的成功模型的趋势是用许多级联在一起的较小卷积(通常为3x3大小)替换所有大型过滤器。 如前所述,这样做有两个巨大的好处。 它不仅减少了参数的数量,而且还增加了网络中非线性的深度和数量,这对于增加其学习能力是一件好事。
替代3x3卷积
也可以通过称为瓶颈的机制来简化3x3卷积。 与早期相似,这将具有正常3x3卷积的相同表示,但参数更少,非线性更多。
瓶颈通过使用以下C过滤器替换3x3卷积层而起作用:
- 带有
C / 2过滤器的1x1卷积 - 带有
C / 2过滤器的3x3卷积 - 带有
C过滤器的1x1卷积
这里给出一个实际的例子:
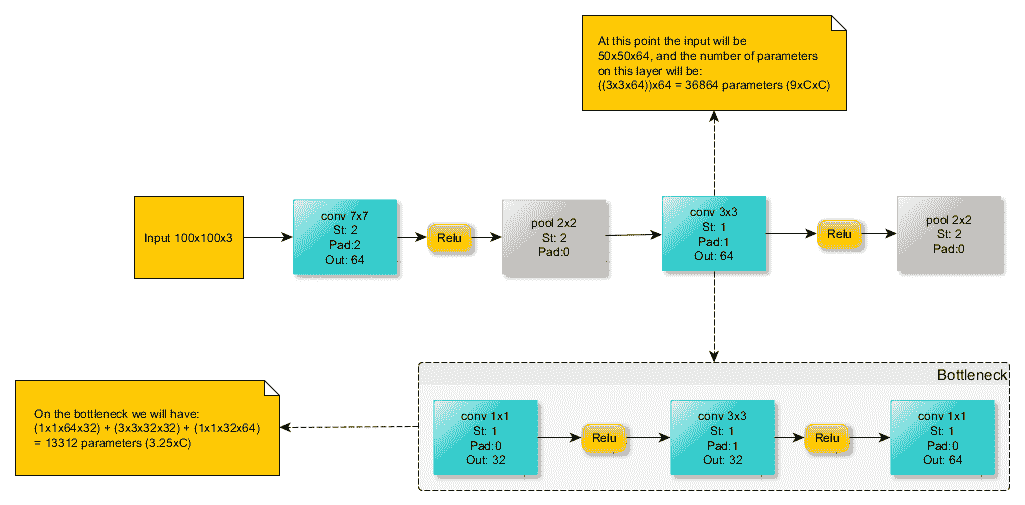
从此示例中,我们将计算参数数量以显示该瓶颈的减少量。 我们得到以下内容:

这比仅使用3x3卷积层时得到的参数要少:
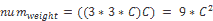
一些网络架构,例如残差网络(我们将在后面看到),使用瓶颈技术再次减少了参数数量并增加了非线性。
VGGNet
VGGNet 由牛津大学的视觉几何组(VGG)创建,是真正引入堆叠更多层的想法的首批架构之一。 虽然 AlexNet 最初以其七层出现时被认为很深,但与 VGG 和其他现代架构相比,这现在已经很小了。
与只有11x11的 AlexNet 相比,VGGNet 仅使用空间大小为3x3的非常小的过滤器。 这些3x3卷积过滤器经常散布在2x2最大池化层中。
使用如此小的过滤器意味着可见像素的邻域也非常小。 最初,这可能给人的印象是,本地信息是模型所考虑的全部内容。 但是,有趣的是,通过依次堆叠小型过滤器,它提供了与单个大型过滤器相同的“感受域”。 例如,堆叠三批3x3过滤器将具有与一个7x7过滤器相同的感受域。
堆叠过滤器的这种洞察力带来了能够拥有更深的结构(我们通常会看到更好的结构)的优点,该结构保留了相同的感受域大小,同时还减少了参数数量。 本章后面将进一步探讨这个想法。
架构
接下来,我们将看到 VGGNet 的架构,特别是包含 16 层的 VGG-16 风格。 所有卷积层都有空间大小为3x3的过滤器,并且随着我们深入网络,卷积层中过滤器的数量从 64 个增加到 512 个。
堆叠两个或三个卷积层然后合并的简单模块化设计使网络的大小易于增加或减小。 结果,VGG 成功创建并测试了具有 11、13 和 19 层的版本:

参数和内存计算
VGG 最酷的功能之一是,由于其在 conv 层中的内核较小,因此使用的参数数量很少。 如果我们从第 2 章,“深度学习和卷积神经网络”记住,卷积层中的参数数量(减去偏差)可以计算如下:

因此,例如,第一层将具有以下参数:
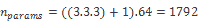
但是要注意,当涉及到模型末端的完全连接(密集)层时,这种数量很少的参数并不是这种情况,通常这是我们可以找到许多模型参数的地方。 如果像在 VGGNet 中一样,一个接一个地堆叠多个密集层,则尤其如此。
例如,第一个密集层将具有以下数量的参数:

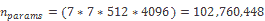
到那时为止,这是所有参数的六倍以上!
如前所述,您需要在训练数据集中使用大量样本来消耗模型参数,因此最好避免过度使用全连接层来避免参数爆炸。 幸运的是,人们发现,如果最后只有一层而不是三层,那么 VGGNet 的工作原理几乎相同。 因此,删除这些全连接层会从模型中删除大量参数,而不会大大降低表现。 因此,如果您决定实现 VGGNet,我们建议您也这样做。
代码
接下来,我们介绍负责在 Tensorflow 中构建 VGG-16 模型图的函数。 像本章中的所有模型一样,VGGNet 旨在对 Imagenet 挑战的 1,000 个类别进行分类,这就是为什么该模型输出大小为 1000 的向量的原因。 显然,可以为您自己的数据集轻松更改此设置,如下所示:
def build_graph(self):
self.__x_ = tf.placeholder("float", shape=[None, 224, 224, 3], name='X')
self.__y_ = tf.placeholder("float", shape=[None, 1000], name='Y')
with tf.name_scope("model") as scope:
conv1_1 = tf.layers.conv2d(inputs=self.__x_, filters=64, kernel_size=[3, 3],
padding="same", activation=tf.nn.relu)
conv2_1 = tf.layers.conv2d(inputs=conv1_1, filters=64, kernel_size=[3, 3],
padding="same", activation=tf.nn.relu)
pool1 = tf.layers.max_pooling2d(inputs=conv2_1, pool_size=[2, 2], strides=2)
conv2_1 = tf.layers.conv2d(inputs=pool1, filters=128, kernel_size=[3, 3],
padding="same", activation=tf.nn.relu)
conv2_2 = tf.layers.conv2d(inputs=conv2_1, filters=128, kernel_size=[3, 3],
padding="same", activation=tf.nn.relu)
pool2 = tf.layers.max_pooling2d(inputs=conv2_2, pool_size=[2, 2], strides=2)
conv3_1 = tf.layers.conv2d(inputs=pool2, filters=256, kernel_size=[3, 3],
padding="same", activation=tf.nn.relu)
conv3_2 = tf.layers.conv2d(inputs=conv3_1, filters=256, kernel_size=[3, 3],
padding="same", activation=tf.nn.relu)
conv3_3 = tf.layers.conv2d(inputs=conv3_2, filters=256, kernel_size=[3, 3],
padding="same", activation=tf.nn.relu)
pool3 = tf.layers.max_pooling2d(inputs=conv3_3, pool_size=[2, 2], strides=2)
conv4_1 = tf.layers.conv2d(inputs=pool3, filters=512, kernel_size=[3, 3],
padding="same", activation=tf.nn.relu)
conv4_2 = tf.layers.conv2d(inputs=conv4_1, filters=512, kernel_size=[3, 3],
padding="same", activation=tf.nn.relu)
conv4_3 = tf.layers.conv2d(inputs=conv4_2, filters=512, kernel_size=[3, 3],
padding="same", activation=tf.nn.relu)
pool4 = tf.layers.max_pooling2d(inputs=conv4_3, pool_size=[2, 2], strides=2)
conv5_1 = tf.layers.conv2d(inputs=pool4, filters=512, kernel_size=[3, 3],
padding="same", activation=tf.nn.relu)
conv5_2 = tf.layers.conv2d(inputs=conv5_1, filters=512, kernel_size=[3, 3],
padding="same", activation=tf.nn.relu)
conv5_3 = tf.layers.conv2d(inputs=conv5_2, filters=512, kernel_size=[3, 3],
padding="same", activation=tf.nn.relu)
pool5 = tf.layers.max_pooling2d(inputs=conv5_3, pool_size=[2, 2], strides=2)
pool5_flat = tf.reshape(pool5, [-1, 7 * 7 * 512])
# FC Layers (can be removed)
fc6 = tf.layers.dense(inputs=pool5_flat, units=4096, activation=tf.nn.relu)
fc7 = tf.layers.dense(inputs=fc6, units=4096, activation=tf.nn.relu)
# Imagenet has 1000 classes
fc8 = tf.layers.dense(inputs=fc7, units=1000)
self.predictions = tf.nn.softmax(self.fc8, name='predictions')
VGG 的更多信息
2014 年,VGG 在 Imagenet 分类挑战中获得第二名,在 Imagenet 定位挑战中获得第一名。 正如我们所看到的,VGGNet 的设计选择是堆叠许多小的卷积层,从而可以实现更深的结构,同时具有更少的参数(如果我们删除了不必要的全连接层),则表现更好。 这种设计选择在创建强大而高效的网络方面非常有效,以至于几乎所有现代架构都复制了这种想法,并且很少(如果有的话)使用大型过滤器。
事实证明,VGG 模型可以在许多任务中很好地工作,并且由于其简单的架构,它是开始尝试或适应问题需求的理想模型。 但是,它确实有以下问题需要注意:
- 通过仅使用
3x3层,尤其是在第一层,计算量不适用于移动解决方案 - 如前几章所述,由于逐渐消失的梯度问题,甚至更深的 VGG 结构也无法正常工作
- 原始设计中大量的 FC 层在参数方面是过大的,这不仅减慢了模型的速度,而且更容易出现过拟合的问题
- 使用许多池化层,目前认为这不是好的设计
GoogLeNet
虽然 VGGNet 在 2014 年 Imagenet 分类挑战赛中排名第二,但我们将要讨论的下一个模型 GoogLeNet 在那一年是赢家。 它是由 Google 创建的,它引入了一种重要的方法来使网络更深,同时减少参数数量。 他们称他们提出了Inception 模块。 该模块填充了大部分 GoogLeNet 模型。
GoogLeNet 具有 22 层,参数几乎比 AlexNet 少 12 倍。 因此,除了更加精确之外,它还比 AlexNet 快得多。 创建Inception模块的动机是制作更深的 CNN,以便获得高度准确的结果,并使该模型可在智能手机中使用。 为此,在预测阶段,计算预算大约需要增加 15 亿次:

Inception 模块
起始模块(或层的块)旨在覆盖较大的区域,但也保持较高的分辨率,以便也可以在图像中查看重要的本地信息。 除了创建更深的网络外,起始块还引入了并行卷积的思想。 我们的意思是在前一层的输出上执行不同大小的并行卷积。
初始层的幼稚视图可以在这里看到:
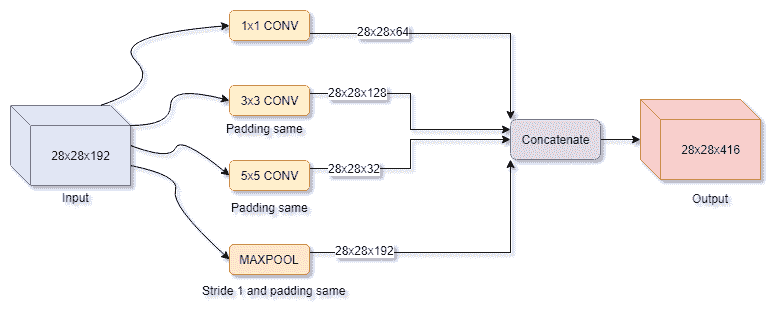
基本上,初始块的想法是使用所有可用的内核大小和操作来覆盖尽可能多的信息,并让反向传播根据您的数据决定使用什么。 在上图中看到的唯一问题是计算成本,因此该图在实践中会有所不同。
考虑我们之前看到的5x5分支,让我们检查一下它的计算成本:

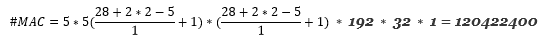
现在,考虑以下更改; 我们添加一个1x1卷积来将5x5卷积输入深度从 192 转换为 16:


如果您观察到,现在计算效率提高了 10 倍。 1x1层会挤压大量深度(瓶颈),然后发送到5x5卷积层。
考虑到这一瓶颈变化,真正的初始层要复杂一些:
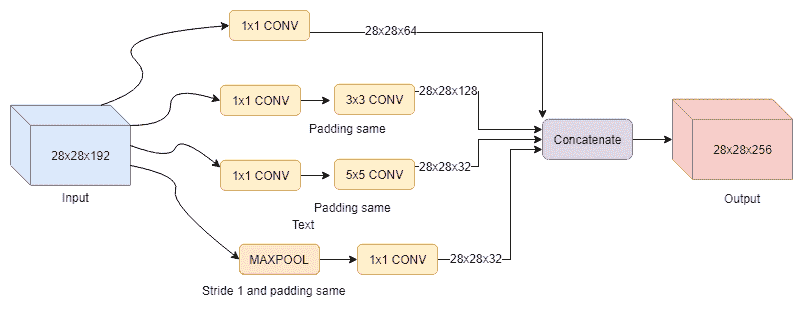
此外,在某些实现中,您可能会注意到有人试图在初始代码块中使用批量规范化或丢弃法。
Googlenet 将只是许多级联的启动块。 在这段代码中,我们展示了如何创建一个起始块:
# Reference: https://github.com/khanrc/mnist/blob/master/inception.py
import tensorflow as tf
def inception_block_a(x, name='inception_a'):
# num of channels: 384 = 96*4
with tf.variable_scope(name):
# Pooling part
b1 = tf.layers.average_pooling2d(x, [3,3], 1, padding='SAME')
b1 = tf.layers.conv2d(inputs=b1, filters=96, kernel_size=[1, 1], padding="same", activation=tf.nn.relu)
# 1x1 part
b2 = tf.layers.conv2d(inputs=x, filters=96, kernel_size=[1, 1], padding="same", activation=tf.nn.relu)
# 3x3 part
b3 = tf.layers.conv2d(inputs=x, filters=64, kernel_size=[1, 1], padding="same", activation=tf.nn.relu)
b3 = tf.layers.conv2d(inputs=b3, filters=96, kernel_size=[3, 3], padding="same", activation=tf.nn.relu)
# 5x5 part
b4 = tf.layers.conv2d(inputs=x, filters=64, kernel_size=[1, 1], padding="same", activation=tf.nn.relu)
# 2 3x3 in cascade with same depth is the same as 5x5 but with less parameters
# b4 = tf.layers.conv2d(inputs=b4, filters=96, kernel_size=[5, 5], padding="same", activation=tf.nn.relu)
b4 = tf.layers.conv2d(inputs=b4, filters=96, kernel_size=[3, 3], padding="same", activation=tf.nn.relu)
b4 = tf.layers.conv2d(inputs=b4, filters=96, kernel_size=[3, 3], padding="same", activation=tf.nn.relu)
concat = tf.concat([b1, b2, b3, b4], axis=-1)
return concat
GoogLeNet 的更多信息
GoogLeNet 的主要优点是,它比 VGG 更为准确,同时使用的参数更少,计算能力也更低。 主要的缺点仍然是,如果我们开始堆叠很多初始层,梯度将消失,而且整个网络具有多个分支和多个损失的设计相当复杂。
残差网络
在前面的部分中,已经证明了网络的深度是有助于提高准确率的关键因素(请参见 VGG)。 TensorFlow 中的第 3 章“图像分类”中也显示,可以通过正确的权重初始化和批量归一化来缓解深度网络中梯度消失或爆炸的问题。 但是,这是否意味着我们添加的层越多,我们得到的系统就越准确? 亚洲研究机构 Microsoft 的《用于图像识别的深度残差学习》的作者发现,只要网络深度达到 30 层,准确率就会达到饱和。 为了解决此问题,他们引入了一个称为残差块的新层块,该块将上一层的输出添加到下一层的输出中(请参见下图)。 残差网络或 ResNet 在非常深的网络(甚至超过 100 层!)中都显示了出色的结果,例如 152 层的 ResNet 赢得了 2015 LRVC 图像识别挑战,其前 5 个测试误差为 3.57。 事实证明,诸如 ResNets 之类的更深层网络要比包括 Inception 模块(例如 GoogLeNet)在内的更广泛的网络更好地工作。

让我们更详细地了解残差块的外观以及其功能背后的直觉。 如果我们有一个输入x和一个输出y,则存在一个将x映射到y的非线性函数H(x)。 假设函数H(x)可以由两个堆叠的非线性卷积层近似。 然后,残差函数F(x) = H(x) - x也可以近似。 我们可以等效地写为H(x) = F(x) + x,其中F(x)表示两个堆叠的非线性层,x标识输入等于输出的函数。
更正式地说,对于通过网络的前向传递,如果x是来自l-2层的张量,并且W[l-1]和W[l]是当前层和先前层的权重矩阵,则下一层l+1的输入y是:
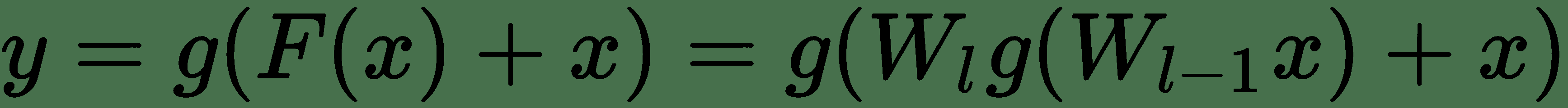
其中g是非线性激活函数,例如 ReLu 和F(x) = W[l] g(W[l-1] x),即两层堆叠卷积。 ReLu 函数可以在添加x之前或之后添加。 剩余的块应由 2 层或更多层组成,因为一层的块没有明显的好处。
为了理解该概念背后的直觉,我们假设我们有一个经过训练的浅层 CNN,其更深的对应层具有与浅层 CNN 相同的层,并且在它们之间随机插入了一些层。 为了拥有一个与浅层模型至少具有相似表现的深层模型,附加层必须近似标识函数。 但是,要学习具有卷积层栈的标识函数比将残差函数推为零要困难得多。 换句话说,如果单位函数是最优解,则很容易实现F(x),因此很容易实现H(x) = x。
另一种思考的方式是,在训练期间,特定的层不仅会从上一层学习一个概念,还会从它之前的其他层学习一个概念。 这比只从上一层学习概念要好。
在实现方面,我们应注意确保x和F(x)的大小相同。
查看残差块的重要性的另一种方法是,我们将为梯度创建一个“高速公路”(加法块),以避免随着梯度的增加而消失的梯度问题!
以下代码将向您展示如何创建残差块,它是残差网络的主要构建块:
# Reference
# https://github.com/tensorflow/tensorflow/blob/master/tensorflow/examples/learn/resnet.py
import tensorflow as tf
from collections import namedtuple
# Configurations for each bottleneck group.
BottleneckGroup = namedtuple('BottleneckGroup',
['num_blocks', 'num_filters', 'bottleneck_size'])
groups = [
BottleneckGroup(3, 128, 32), BottleneckGroup(3, 256, 64),
BottleneckGroup(3, 512, 128), BottleneckGroup(3, 1024, 256)
]
# Create the bottleneck groups, each of which contains `num_blocks`
# bottleneck groups.
for group_i, group in enumerate(groups):
for block_i in range(group.num_blocks):
name = 'group_%d/block_%d' % (group_i, block_i)
# 1x1 convolution responsible for reducing dimension
with tf.variable_scope(name + '/conv_in'):
conv = tf.layers.conv2d(
net,
filters=group.num_filters,
kernel_size=1,
padding='valid',
activation=tf.nn.relu)
conv = tf.layers.batch_normalization(conv, training=training)
with tf.variable_scope(name + '/conv_bottleneck'):
conv = tf.layers.conv2d(
conv,
filters=group.bottleneck_size,
kernel_size=3,
padding='same',
activation=tf.nn.relu)
conv = tf.layers.batch_normalization(conv, training=training)
# 1x1 convolution responsible for restoring dimension
with tf.variable_scope(name + '/conv_out'):
input_dim = net.get_shape()[-1].value
conv = tf.layers.conv2d(
conv,
filters=input_dim,
kernel_size=1,
padding='valid',
activation=tf.nn.relu)
conv = tf.layers.batch_normalization(conv, training=training)
# shortcut connections that turn the network into its counterpart
# residual function (identity shortcut)
net = conv + net
MobileNet
我们将以一个新的 CNN 系列结束本章,该系列不仅具有较高的准确率,而且更轻巧,并且在移动设备上的运行速度更快。
由 Google 创建的 MobileNet 的关键功能是它使用了不同的“三明治”形式的卷积块。 它不是通常的(CONV,BATCH_NORM,RELU),而是将3x3卷积拆分为3x3深度卷积,然后是1x1点向卷积。他们称此块为深度可分离卷积。
这种分解可以减少计算量和模型大小:
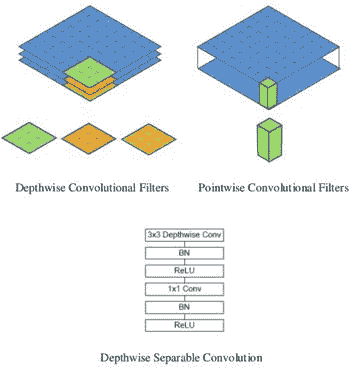
深度可分离卷积
这个新的卷积块(tf.layers.separable_conv2d)由两个主要部分组成:深度卷积层,然后是1x1点式卷积层。 该块与普通卷积有以下几种不同:
- 在正常卷积层中,每个过滤器
F将同时应用于输入通道上的所有通道(F应用于每个通道然后求和) - 这个新的卷积
F分别应用于每个通道,并且结果被级联到某个中间张量(多少由深度倍数DM参数控制)
相对于标准卷积,深度卷积非常有效。 但是,它仅过滤输入通道,并且不将它们组合以创建新功能。
现在,将使用1x1转换层将深度输出张量映射到某些所需的输出通道深度,该转换层将在通常在标准卷积层中发生的通道之间进行混合。 区别在于DM参数可用于丢弃一些信息。 同样,1x1转换仅用于调整音量大小。
控制参数
MobileNets 使用两个超参数来帮助控制精度和速度之间的折衷,从而使网络适合您要定位的任何设备。 这两个超参数如下:
- 宽度倍增器:通过统一减少整个网络中使用的过滤器数量,控制深度卷积精度
- 分辨率倍增器:只需将输入图像缩小到不同大小
MobileNets 的更多信息
对于任何神经网络设计,MobileNets 都具有一些最佳的精度,速度和参数比率。
但是,目前尚无良好(快速)的深度卷积实现可在 GPU 上运行。 结果,训练可能会比使用正常的卷积运算慢。 但是,此网络目前真正发挥作用的地方是小型 CPU 设计,提高的效率更加明显。
总结
在本章中,我们向您介绍了各种卷积神经网络设计,这些设计已经证明了它们的有效性,因此被广泛使用。 我们首先介绍牛津大学 VGG 的 VGGNet 模型。 接下来,在最终讨论微软的残差网络之前,我们先使用 Google 的 GoogLeNet。 此外,我们还向您展示了一种更高级的新型卷积,该模型在名为 MobileNet 的模型设计中具有特色。 在整个过程中,我们讨论了使每个网络如此出色的不同属性和设计选择,例如跳过连接,堆叠小型过滤器或启动模块。 最后,给出了代码,向您展示了如何在 TensorFlow 中写出这些网络。
在下一章中,我们将讨论一种称为生成模型的新型模型,该模型将使我们能够生成数据。
标签:卷积,self,神经网络,图像,tf,TensorFlow,我们 From: https://www.cnblogs.com/apachecn/p/17322087.html