可达性统计
建图 图的存储
拓扑排序:
DAG(有向无环图),往拓扑排序思考。
拓扑排序的目标是将所有节点排序,使得排在前面的节点不能依赖于排在后面的节点。
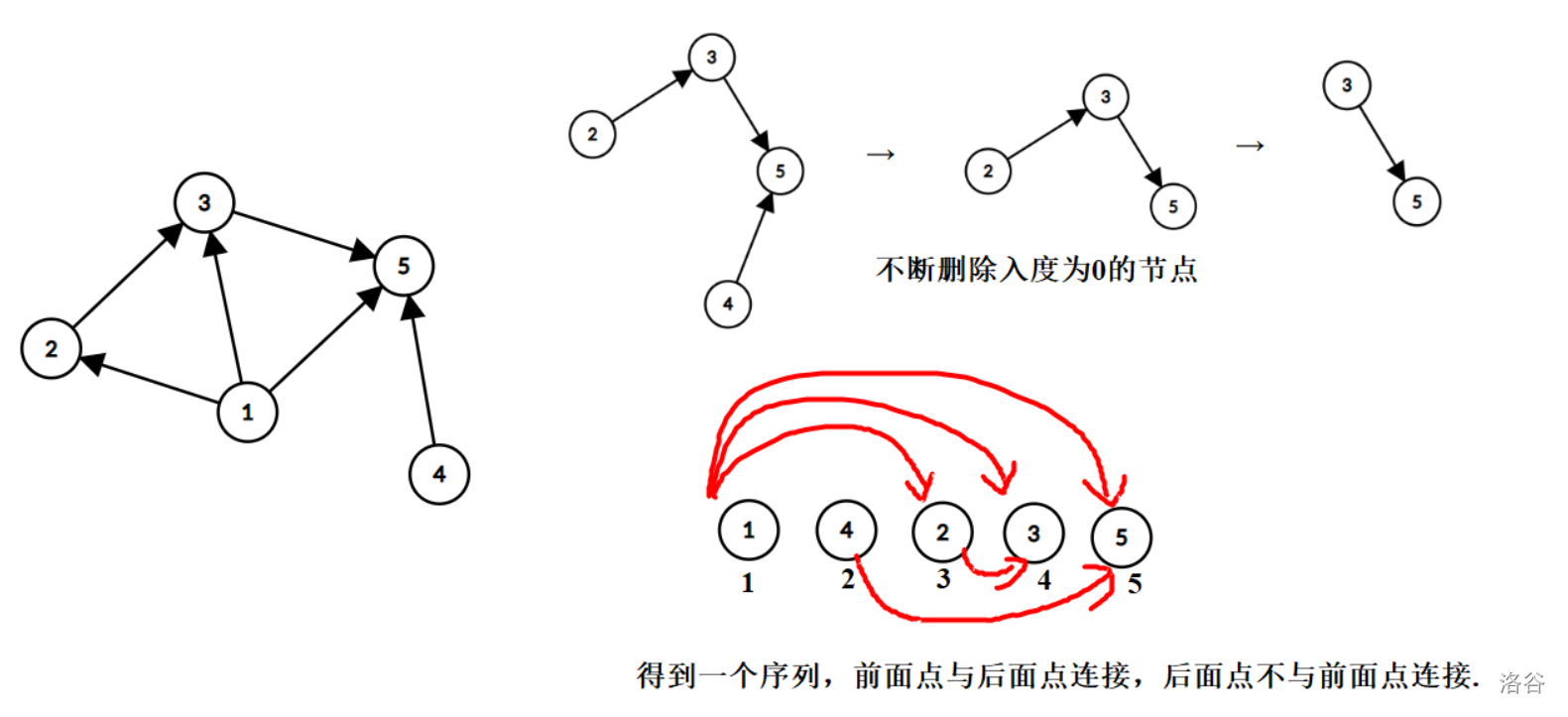
此类问题需要使用bitset优化。
bitset 在 bitset 头文件中,它类似数组,并且每一个元素只能是0或1,每个元素只用1bit空间,可看作几个int拼一起。
2进制位从右向左,bitset是从左向右,与其相反(0~2。
二进制 110
标位:2 1 0
声明
bitset<N> s;//N为长度
单点修改,时间复杂度\(O(1)\)
s[pos]=a;
bitset支持位运算,与或非,效果同int。
bitset绝大部分操作时间复杂度\(O(\frac{N}{w})\)
成员函数:
b.any() b中是否存在置为1的二进制位,有 返回true
b.none() b中是否没有1,没有 返回true
b.count() b中为1的个数
b.size() b中二进制位的个数
b.set() 把b中所有位都置为1
b.set(pos) 把b中pos位置置为1
b.reset() 把b中所有位都置为0,清空
b.reset(pos) 把b中pos位置置为0
b.flip() 把b中所有二进制位取反
b.flip(pos) 把b中pos位置取反
这里,bitset可以看作一个集合,1为可以到达的点,'|' 是把两个集合元素合并(默认不重复。
#include <bits/stdc++.h>
#define cin std::cin
#define cout std::cout
#define endl std::endl
namespace lcj{
const int N=3e4+10;
int n,m,head[N],ne[N],e[N],idx,topo[N],deg[N],cnt;
std::bitset<N> f[N];
std::queue<int> q;
void add(int x,int y){//头插
e[++idx]=y;
ne[idx]=head[x];
head[x]=idx;
}
void main(){
cin>>n>>m;
for(int i=1;i<=m;i++){
int x,y;
cin>>x>>y;
add(x,y);//x→y
deg[y]++;//入度个数
}
for(int i=1;i<=n;i++){//最开始入度为0的点
if(!deg[i]) q.push(i);
}
while(!q.empty()){//BFS实现拓扑排序
int h=q.front();
q.pop();topo[++cnt]=h;
for(int i=head[h];i;i=ne[i]){
int v=e[i];
deg[v]--;
if(!deg[v]) q.push(v);
}
}
for(int i=cnt;i;i--){
int v=topo[i];
f[v].reset();f[v][v]=1;
for(int j=head[v];j;j=ne[j]){
f[v]|=f[e[j]];
}
}
for(int i=1;i<=n;i++){
cout<<f[i].count()<<endl;//1的数量为可到达点的数量
}
}
}
signed main(){
lcj::main();
return 0;
}