题目链接
考虑这棵树在满足条件下是什么样子的?
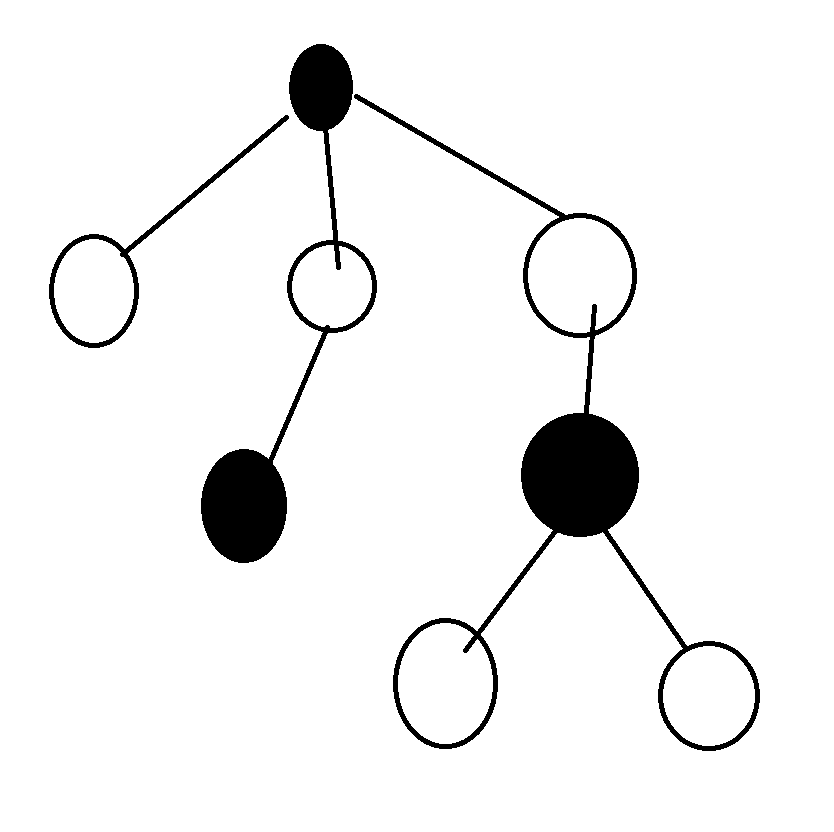
我们发现如果对于一棵树黑白染色,白色表示周围的点大于自身,黑色的点反之,是满足条件的。同时,将黑白点反色也是满足条件的。
我们考虑进行 \(\text{dp}\) ,设 \(dp_{i,j,0/1}\) 表示以点 \(i\) 为根的子树,\(i\) 点权值的排名是 \(j\) ,且 \(i\) 点颜色是黑或白的方案数。
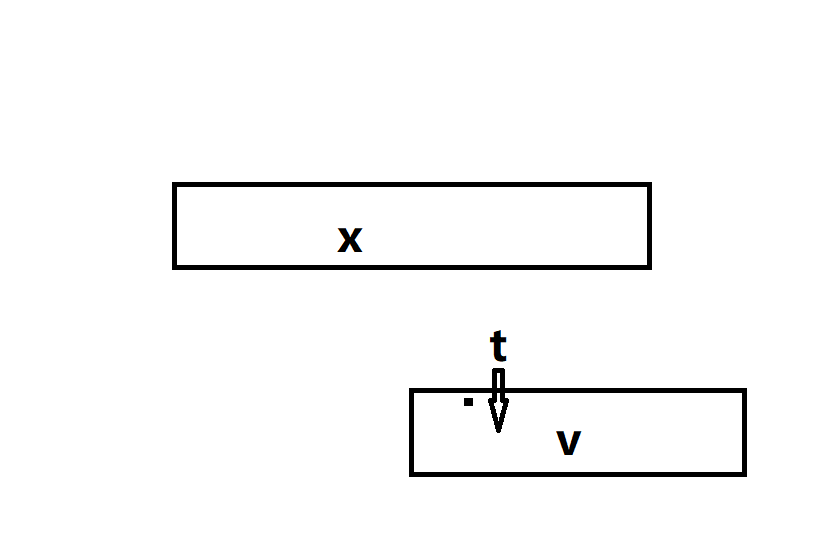
以 \(x\) 点为白点为例,考虑将子树 \(v\) 合并到 \(x\) 的过程中前 \(t\) 个点插入到了 \(x\) 前,剩余的 \(sz[v] - t\) 个点在 \(x\) 后。那么此时转移为
\[dp[x][i+t][1] += \binom{i-1+t}{t} \binom{sz[x]-i+sz[v]-t}{sz[v]-t} \times dp[x][i][1] \times dp[v][j][0] (t \geq j) \]对于 \(x\) 点是黑点的转移同理为
\[dp[x][i+t][0] += \binom{i-1+t}{t} \binom{sz[x]-i+sz[v]-t}{sz[v]-t} \times dp[x][i][0] \times dp[v][j][1] (t \leq j-1) \]此时 \(dp\) 的转移复杂度为 \(O(n^3)\) ,无法通过。
考虑枚举 \(t\) 算所有能转移到 \(t\) 的 \(j\) 的贡献,式子改写为
\[dp[x][i+j][1] += \binom{i-1+j}{j} \binom{sz[x]-i+sz[v]-j}{sz[v]-j} \times dp[x][i][1] \times pre[j] \]\[dp[x][i+j][0] += \binom{i-1+j}{j} \binom{sz[x]-i+sz[v]-j}{sz[v]-j} \times dp[x][i][0] \times suc[j+1] \]其中
\[pre[j]= \sum_{k=1}^{j} dp[v][k][0] \]\[suc[j]= \sum_{k=j+1}^{sz[v]} dp[v][k][1] \]复杂度为 \(O(n^2)\) ,可以通过。
#include<iostream>
#include<cstdio>
#include<string>
#include<cstring>
#include<vector>
#include<algorithm>
using namespace std;
typedef long long ll;
const int mod=998244353;
const int N=3005;
struct node{
int nxt;int to;
}e[N*2];
int head[N],tot;
int n,rx,ry;
int fa[N],sz[N];
int dp[N][N][2],pre[N],suc[N];
int g[N][2],ans;
int fac[N],ifac[N];
inline void read(int &x)
{
int f=1;char c;
for(x=0,c=getchar();c<'0'||c>'9';c=getchar()) if(c=='-') f=-1;
for(;c>='0'&&c<='9';c=getchar()) x=(x<<1)+(x<<3)+(c^48); x*=f;
}
inline int mn(int _x,int _y){return _x<_y?_x:_y;}
inline int mx(int _x,int _y){return _x>_y?_x:_y;}
inline int ab(int _x){return _x<0?-_x:_x;}
inline void add(int from,int to){
e[++tot].to=to;e[tot].nxt=head[from];head[from]=tot;
}
inline int C(int n,int m){
if(n<m) return 0;
return 1ll*fac[n]*ifac[m]%mod*ifac[n-m]%mod;
}
inline int qpow(int base,int cnt){
int rest=1;
while(cnt){
if(cnt&1) rest=1ll*rest*base%mod;
base=1ll*base*base%mod;
cnt>>=1;
}
return rest;
}
inline void dfs(int x){
sz[x]=1;
dp[x][1][0]=dp[x][1][1]=1;
for(int ei=head[x];ei;ei=e[ei].nxt){
int v=e[ei].to;
if(v==fa[x]) continue;
fa[v]=x;dfs(v);
for(int j=0;j<=sz[v]+1;j++) pre[j]=suc[j]=0;
for(int j=1;j<=sz[v];j++) pre[j]=(pre[j-1]+dp[v][j][0])%mod;
for(int j=sz[v];j>=1;j--) suc[j]=(suc[j+1]+dp[v][j][1])%mod;
for(int i=1;i<=sz[x];i++){
for(int j=0;j<=sz[v];j++){
g[i+j][0]=(g[i+j][0]+1ll*C(i-1+j,j)*C(sz[x]-i+sz[v]-j,sz[v]-j)%mod*dp[x][i][0]%mod*suc[j+1]%mod)%mod;
g[i+j][1]=(g[i+j][1]+1ll*C(i-1+j,j)*C(sz[x]-i+sz[v]-j,sz[v]-j)%mod*dp[x][i][1]%mod*pre[j]%mod)%mod;
}
}
sz[x]+=sz[v];
for(int i=0;i<=sz[x];i++){
dp[x][i][0]=g[i][0];dp[x][i][1]=g[i][1];
g[i][0]=g[i][1]=0;
}
}
// for(int i=1;i<=sz[x];i++) printf("dp[%d][%d] [0]=%d [1]=%d\n",x,i,dp[x][i][0],dp[x][i][1]);
return ;
}
int main()
{
read(n);
for(int i=1;i<n;i++){
read(rx);read(ry);
add(rx,ry);add(ry,rx);
}
fac[0]=1;for(int i=1;i<=n+1;i++) fac[i]=1ll*i*fac[i-1]%mod;
ifac[n+1]=qpow(fac[n+1],mod-2);
for(int i=n;i>=0;i--) ifac[i]=1ll*(i+1)*ifac[i+1]%mod;
dfs(1);
for(int i=1;i<=n;i++){
ans=(ans+dp[1][i][0])%mod;
ans=(ans+dp[1][i][1])%mod;
}
printf("%d\n",ans);
return 0;
}