昨天模拟赛考了 \(IDA^*\) 然后愣是没写出来暴力,感觉自己的搜索是时候该好好练一下了啊QAQ。
upd:本来只打算写一下 \(ID\) 、 \(A^*\) 、模拟退火、01bfs,双向bfs、爬山法和遗传算法的,后面想起来之前和在一个哥哥那里听过的一致代价搜索,稍微学习了一下 ,等有空的时候再写。
迭代加深搜索(\(\text{ID}\))
ID算法适合一些搜索树层数可能很大的题目,如从某个起点到达某位置,将某个数字分解为若干数字之类的问题。
例如现在我们有一个分解问题。
若该问题分解要求得的是最小分解总数,那么我们不难想到 \(bfs\) 。
显然 \(bfs\) 所需的空间过大,若情况数过多,我们便转向考虑用 \(dfs\) ,但如果我们想要求得最优解即最大/小分解总数就需要枚举所有的情况,然后再取 \(\min/\max\) 值,在时间复杂度上又不如 \(bfs\) 。
于是我们考虑一种新的做法:
- 首先我们先仿照二分答案为我们的 \(dfs\) 设置一个分解总数上/下界 。(这里如果求的是最大分解总数则设下界,反之则设下界。)
- 然后我们进行搜索验证上/下界是否合理即我们能否达到该上/下界。
- 若可以,因为我们的界是从大到小/从小到大枚举的(下面再说为什么),所以当前的界即为我们求得的最大/小分解总数。
搜索中可以适当加上一些剪枝。
经过上面的阐述我们 (也可能只有我自己) 发现 \(ID\) 的过程与二分答案的过程极其相似,似乎同样都是:
-
枚举答案
-
验证答案
那么这是否意味着我们枚举上下界的时候也是二分枚举呢?
答案是一定不。
我们观察下图。
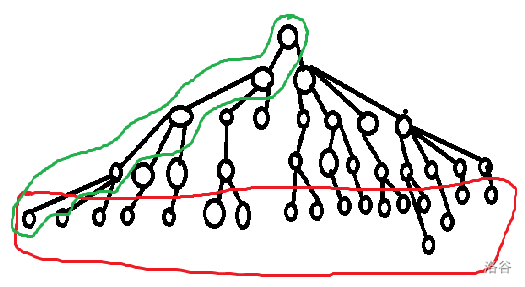
我们发现在一棵 \(n\) 层的搜索树中,我们可将树的每一层的节点数看作底数近似为定值,指数严格单调递增的 \(n\) 个公比 \(\geq 2\) 的似等比数列项。
此时我们易发现,对于等比数列的第 \(i\) 项,它大概率符合下式:
- \(num_i=a^{dfs\_step}\geq \sum\limits_{j=1}^{dfs\_step-1}num_j=\dfrac{num_0-(1-q^{dfs\_step})}{1-q}\)
\(\operatorname{PS}:\) 为什么要说是大概率嘞?
因为每一层的底数其实是不一定的,特别是当我们进行一定的剪枝之后,其实这棵搜索树的节点数是远小于原树的节点数的,但是我们现在考虑的是不优的情况,所以 要记得好好剪枝 我们现在将树的每一层都看作等比数列项来讨论。
也就是说,在不优的情况下,我们的搜索树每增加一层,树的结点就有可能会增加到原来的两倍甚至更多,那么此时显然我们是希望树的层数越少越好。
而二分枚举层数显然一开始就有可能枚举到一个很大的层数而使得我们 \(TLE\) ,所以我们的上/下界显然要按顺序/逆序来枚举,对时间的优化才更大。
顺带提一嘴,我们看回上面的图来进一步理解一下为什么 \(ID\) 算法相当于 \(bfs\) 的时间+ \(dfs\) 的空间:
-
显然我们在使用 \(ID\) 算法时只需要 \(dfs\) 存储图中的一条链即可,而 \(bfs\) 则最少需要存储最底层的所有结点,空间显然是 \(ID\) 采用的 \(dfs\) 更优。
-
而我们按序枚举的上下界实际上就相当于 \(bfs\) 中的保证第一次找到的分解方案一定最优。
ok,没了。
例题:
\(\text{A}^*\)(启发式搜索)
碎碎念
我至今没太搞懂启发式搜索跟 \(A^*\) 的清晰界限在哪里.....
暂且把启发式搜索当做一种思想、把 \(A^*\) 当做这种思想的一种具体实现吧...... QwQ
正文
启发式搜索
启发式搜索在我看来是一种贪心思想。(?
概述:
- 启发式搜索就是在搜索过程中对当前状态到达目标状态所需要的代价进行估值,然后与目前已经求得的到达目标的最小代价进行比较。
- 若我们当前的估值已经大于目前已经求得的最小代价了,那当然是果断剪枝 \(return\) 啦。
\(A^*\)算法
我们定义当前状态到达目标状态估计需要的代价为函数 \(h()\),且从起点到达当前状态的实际代价为函数 \(g()\)。
看完上面对启发式搜索的概述,我们不难得到一个细节:
- 当前状态到达目标状态的估计代价 \(h()\) 必须要保证小于等于 实际到达目标状态的代价。
为什么?因为我靠它剪枝。
如果我们的 \(h()\) 不能保证小于等于实际代价,那么当我们当前跑到了一个比之前所有的状态代价更小的状态时,若您人品极佳 \(h()\) 这个时候没出岔子那请您出门左拐, 若此时我们的估值函数 \(h()\) 刚好比实际情况要大,且加上到达这个状态已经消耗的代价得到的估计总代价大于之前的得到的所有方案的最小代价,即:
-
\(g()+\) 当前状态到达目标状态的实际最小代价 \(<ans\),即从当前状态到达目标状态可以得到更小的代价。
-
\(g()+h()>ans\),此时因为启发式搜索的剪枝操作我们会选择 \(return\) 而不是继续搜下去。其中 \(ans\) 为我们的搜索到目前为止能得到的最小代价。
-
此时我们就会因为我们的估值错误而错将更小代价的方案当作非更优方案剪枝掉。
所以 \(A^*\) 算法的核心就在我们需要根据题目设计一个保证小于等于实际代价的估计代价 \(h()\) 。
且在保证上一条件的情况下,我们的估值函数 \(h()\) 与实际代价的接近程度将决定 \(A^*\) 的性能,估值越准确,我们能够剪枝掉的状态就越多,搜索的效率也就越快。
上文我们所说的 \(A^*\) 与启发式搜索看上去似乎只是简单的估值剪枝罢了,但是实际上的 \(A^*\) 并非仅此而已。
认识真正的 \(A^*\) 算法
说得好像上面的 \(A^*\) 是假的一样。
\(A^*\) 的核心在于估值函数。
那么我们其实就可以把每一个状态的估计代价作为其权值放入一个优先队列里面,然后像 \(bfs\) 一样每次搜索到一个点之后将其拓展点加入优先队列。
若我们当前搜索到的状态已经是目标状态,因为优先队列的有序性,所以到达当前状态的代价一定是到达目标代价的最小代价,故我们可以直接输出当前状态的代价,然后退出搜索。
\(\text{IDA}^*\)
刚刚讲完了 \(A^*\) 和 \(ID\) 两种搜索,我们不难总结出其核心:
-
\(A^*\) :设计一个尽量接近但恒小于等于实际代价的估值函数 \(h()\) ,用其进行减枝/有序的搜索(优先搜索估计代价更小的状态)。
-
\(ID\) :从小到大枚举dfs的最大层数,然后dfs验证在此层数限制内是否有解,若有解,则当前枚举到的最大层数即为到达目标状态的最小代价。
那么将两者结合起来的话,我们其实可以将 \(ID\) 的枚举最大层数和 \(A^*\) 的估值剪枝结合起来,即:
for(i:0~ans)
if(dfs(0,maxdep))
printf(maxdep);
//若在该层数限制下dfs能够达到目标状态,则此时枚举到的层数就是我们要求的最小代价
bool dfs(step,maxdep){
if(step==maxdep)
return judge(now_state);//判断当前状态是否为目标状态
if(step+h()>maxdep) return 0;
//若当前的未达到目标状态,且我们估计的代价已经大于最大层数,那么直接剪枝就行了
for(枚举每一种新的状态){
//常规dfs的一些处理
if(dfs(step+1,maxdep)) return 1;//如果已经找到了目标状态,则不用继续搜了
//常规dfs操作
}
return 0;//若无法通过此状态达到目标状态,则返回false
}