树状数组

简介

树状数组是一种用于维护 \(n\) 个数的区间和的数据结构。
一般能用树状数组做的题，都可以使用线段树来做。相较于码量，树状数组的码量要比线段树少许多，不过相对应的，它所能实现的功能没有线段树多。

好的，不多说废话，下面进入正题。

例题 1：P3374【模板】树状数组 1

例题 2：P3368【模板】树状数组 2

操作

现在我们已知数列 \(a_i\)。

\(\text{lowbit}\)

\(\text{lowbit(x)}\) 表示 \(x\) 表示的二进制中最低的一位 \(1\) 所表示的数，举个例子：\(4\) 的二进制为 \(100_{(2)}\)，那么 \(\text{lowbit(4)} = 100_{(2)} = 4\)；\(12\) 的二进制为 \(1100_{(2)}\)，那么 \(\text{lowbit(12)} = 100_{(2)} = 4\)。

怎么求呢？我们知道 \(-x\) 的补码为 \(x\) 按位取反再 \(+1\)，大家可以自行举例模拟，会发现最低的一位 \(1\) 所表示的数其实就是 \(x \& (-x)\)。

Code:

int lowbit(int x) {
	return x & (-x);
}

\(\text{lowbit}\) 是树状数组的核心操作，为后面的操作奠定了基础。

\(\text{区间查询}\)

我们令 \(tr_i = \sum_{j = i - \text{lowbit(i)} + 1}^{i} a_i\)

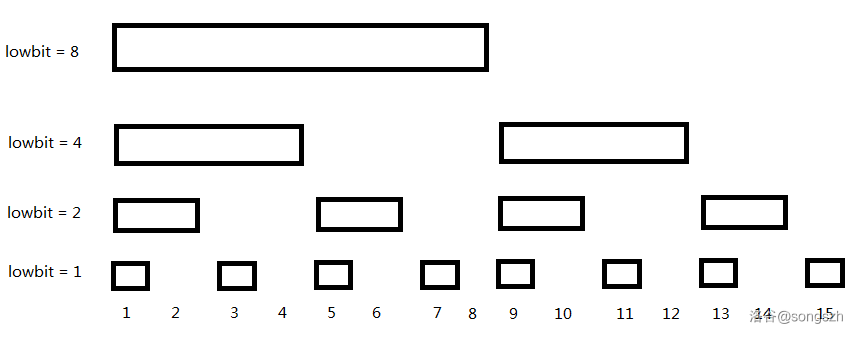
如上图，我们假设要求 \(a_l\) 到 \(a_r\)，可以将 \(tr_r\) 加入 \(res\)（query 的值），然后我们就需要求 \(a_l\) 到 \(a_{r - \text{lowbit(r)}}\)，再将 \(tr_{r - \text{lowbit(r)}}\) 加入 \(res\dots\)

以此类推，我们就可以得到以下操作。

Code:

int sum(int x) {
	int res = 0;
	for (int i = x; i; i -= lowbit(x) ) res += tr[i];
	return res;
}

答案为 sum(y) - sum(x - 1)。

\(\text{单点查询}\)

与 \(\text{区间查询}\) 一样，只不过最后的答案变为了 sum(x)。

\(\text{单点修改}\)

修改与查询其实是反着来的，相对应的，\(a_i\) 改变了，\(a_{i + \text{lowbit(i)}}\) 也会跟着改变，那么可以得到以下代码。

Code:

int add(int x,int k) {
	for (int i = x; i <= n; i += lowbit(x) ) tr[i] += k;
}

\(\text{区间修改}\)

这时一定有人会有疑问：单点修改这么做，那区间修改呢？

其实非常简单，假设我们要修改 \(a_l\) 到 \(a_r\)，那么我们可以先将 \(a_l\) 到 \(a_n\) 加上 \(k\)，再将 \(a_{r + 1}\) 到 \(a_n\) 减去 \(k\)，即为我们将 \(a_l\) 到 \(a_r\) 都加上了 \(k\)。（此处以加 \(k\) 为例）

那么区间修改其实就是 add(x,k),add(y + 1,-k)。

Code

AC Code of P3374【模板】树状数组 1

#include <bits/stdc++.h>

#define int long long

using namespace std;

const int N = 5e5 + 10;

int n,m;
int tr[N];

inline int read() {
	int x = 0,f = 1;
	char ch = getchar();
	while (ch < '0' || ch > '9') {
		if (ch == '-') f = -1;
		ch = getchar();
	}
	while (ch >= '0' && ch <= '9') {
		x = x * 10 + ch - 48;
		ch = getchar();
	}
	return x * f;
}

int lowbit(int x) {
	return x & (-x);
}

int add(int x,int k) {
	for (int i = x; i <= n; i += lowbit(i) ) tr[i] += k;
}

int sum(int x) {
	int res = 0;
	for (int i = x; i; i -= lowbit(i) ) res += tr[i];
	return res;
}

signed main() {
	ios :: sync_with_stdio(false);
	n = read();
	m = read();
	for (int i = 1; i <= n; ++ i ) add(i,read());
	while (m -- ) {
		int op = read(),x = read(),k = read();
		if (op == 1) add(x,k);
		else cout << sum(k) - sum(x - 1) << endl;
	}
	return 0;
}

AC Code of P3368【模板】树状数组 2

#include <bits/stdc++.h>

#define int long long

using namespace std;

const int N = 5e5 + 10;

int n,m;
int tr[N];

inline int read() {
	int x = 0,f = 1;
	char ch = getchar();
	while (ch < '0' || ch > '9') {
		if (ch == '-') f = -1;
		ch = getchar();
	}
	while (ch >= '0' && ch <= '9') {
		x = x * 10 + ch - 48;
		ch = getchar();
	}
	return x * f;
}

int lowbit(int x) {
	return x & (-x);
}

int add(int x,int k) {
	for (int i = x; i <= n; i += lowbit(i) ) tr[i] += k;
}

int sum(int x) {
	int res = 0;
	for (int i = x; i; i -= lowbit(i) ) res += tr[i];
	return res;
}

signed main() {
	ios :: sync_with_stdio(false);
	n = read();
	m = read();
	for (int i = 1; i <= n; ++ i ) {
		int x = read();
		add(i,x),add(i + 1,-x);
	}
	while (m -- ) {
		int op = read(),x,y,k;
		if (op == 1) {
			x = read(); y = read(); k = read();
			add(x,k);
			add(y + 1,-k);
		} else {
			x = read();
			cout << sum(x) << endl;
		}
	}
	return 0;
}

写 blog 不易，请点个赞。

祝你理解树状数组。

作者：\(\text{songszh}\)