本文已收录到 AndroidFamily,技术和职场问题,请关注公众号 [彭旭锐] 提问。
大家好,我是小彭。
上周末是 LeetCode 第 338 场周赛,你参加了吗?这场周赛覆盖的知识点很多,第四题称得上是近期几场周赛的天花板。
小彭的技术交流群 02 群来了,公众号回复 “加群” 加入我们~
目录
2599. K 件物品的最大和(Easy)
- 贪心、模拟 $O(1)$
2600. 质数减法运算(Medium)
- 题解一:暴力枚举 + 二分查找 $O(U\sqrt{U} + nlgU)$
- 题解二:Eratosthenes 埃氏筛 + 二分查找 $O(UlgU + nlgU)$
- 题解三:Euler 欧氏线性筛 + 二分查找 $O(U + nlgU)$
2601. 使数组元素全部相等的最少操作次数
- 前缀和 + 二分查找 $O(nlgn + qlgn)$
2602. 收集树中金币(Hard)
- 拓扑排序 + 模拟 $O(n)$

2599. K 件物品的最大和(Easy)
题目地址
https://leetcode.cn/problems/k-items-with-the-maximum-sum/description/
题目描述
袋子中装有一些物品,每个物品上都标记着数字 1 、0 或 -1 。
给你四个非负整数 numOnes 、numZeros 、numNegOnes 和 k 。
袋子最初包含:
numOnes件标记为1的物品。numZeroes件标记为0的物品。numNegOnes件标记为1的物品。
现计划从这些物品中恰好选出 k 件物品。返回所有可行方案中,物品上所标记数字之和的最大值。

题解(贪心 + 模拟)
简单模拟题,优先选择 1,其次 0,最后 -1。
class Solution {
fun kItemsWithMaximumSum(numOnes: Int, numZeros: Int, numNegOnes: Int, k: Int): Int {
var x = k
// 1
val oneCnt = Math.min(numOnes, x)
x -= oneCnt
if (x == 0) return oneCnt
// 0
x -= Math.min(numZeros, x)
if (x == 0) return oneCnt
// -1
return oneCnt - x
}
}
复杂度分析:
- 时间复杂度:$O(1)$
- 空间复杂度:$O(1)$
2600. 质数减法运算(Medium)
题目地址
https://leetcode.cn/problems/prime-subtraction-operation/description/
题目描述
给你一个下标从 0 开始的整数数组 nums ,数组长度为 n 。
你可以执行无限次下述运算:
- 选择一个之前未选过的下标
i,并选择一个 严格小于nums[i]的质数p,从nums[i]中减去p。
如果你能通过上述运算使得 nums 成为严格递增数组,则返回 true ;否则返回 false 。
严格递增数组 中的每个元素都严格大于其前面的元素。

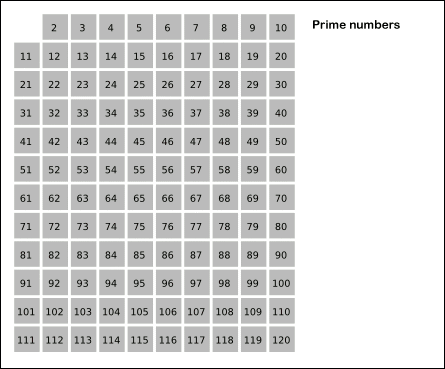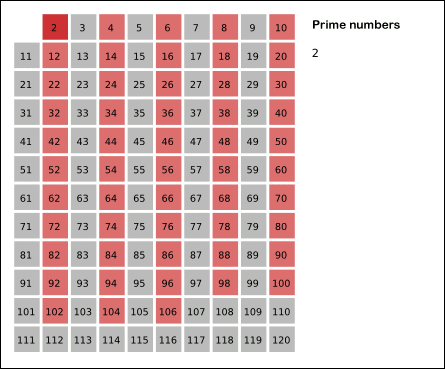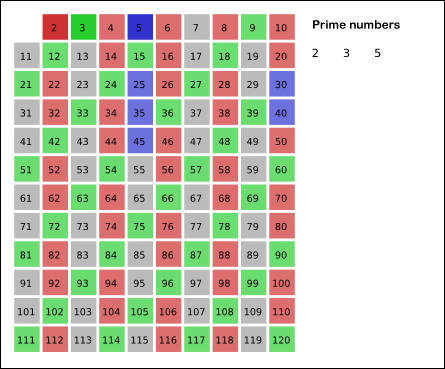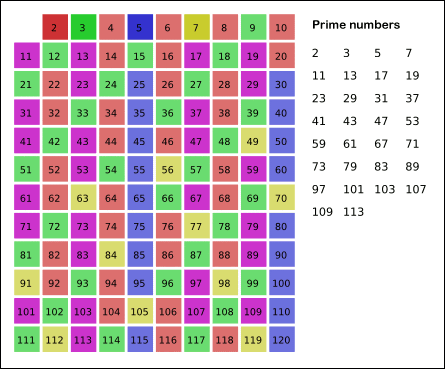
预备知识
这道题如果熟悉质数筛就是简单二分查找问题。
1、质数定义:
- 质数 / 素数:只能被 1 和本身整除的数,例如 3,5,7;
- 合数:除了能被 1 和本身整除外,还能被其他数整除的数。也可以理解为由多个不为 1 的质数相乘组成的数,例如 4 = 2 _ 2,6 = 2 _ 3。
- 1 既不是质数也不是合数。
2、判断 x 是否为质数:
可以枚举 [2,n-1] 的所有数,检查是否是 x 的因数,时间复杂度是 O(n)。事实上并不需要枚举到 n-1:以 n = 17 为例,假设从 2 枚举到 4 都没有发现因子,我们发现 5 也没必要检查。
可以用反证法证明:如果 17 能够被 5 整除,那么一定存在 17 能够被 17/5 的另一个数整除。而由于 17/5 < 5 与前面验证过 [2,4] 不存在因子的前提矛盾。因此 5 不可能是因子。
由此得出,如果存在整除关系 n/x = y,我们只需要检查 x 和 y 之间的较小值。所有的较小值最大不会超过 n 的平方根。所以我们可以缩小检查范围,只检查 $[1, O(\sqrt{x})]$,时间复杂度是 $O(\sqrt{x})$
3、计算所有小于 n 的质数,有三种算法:
- 暴力枚举: 枚举每个数,判断它是不是质数,整体时间复杂度是 $O(n\sqrt{n})$
- Eratosthenes 埃氏筛: 如果 x 不是质数,则从 x*x 开始将成倍的数字标记为非质数,整体时间复杂度是 O(UlgU);
- Euler 欧氏线性筛: 标记 x 与 “小于等于 x 的最小质因子的质数” 的乘积为非质数,保证每个合数只被标记最小的质因子标记。
题解一(暴力枚举质数 + 二分查找)
为了获得严格递增数组,显然数组的末位元素的约束是最弱的,甚至是没有约束的。所以我们选择从后往前处理,最后一个数不需要处理。
显然如果靠后的元素尽可能大,那么靠前的元素越容易满足条件。因此,我们可以找到贪心思路:从后往前处理,每处理一个数字时,我们尽可能减去满足题目要求的最小质数,减缓数字变小的速度,给靠前的数字留出空间。
容易发现,“满足题目要求的最小质数” 存在单调性可以用二分查找解决。因此我们的题解分为 2 部分:
- 1、预处理题目数据范围内的所有质数,即小于 1000 的质数列表,可以用预置知识中的两种;
- 2、使用二分查找寻找 “满足题目要求的最小质数”。
class Solution {
companion object {
// 1000 以内的质数列表
private val primes = getPrimes(1000)
// 暴力求质数
private fun getPrimes(max: Int): IntArray {
val primes = LinkedList<Int>()
for (num in 2..max) {
if (isPrime(num)) primes.add(num)
}
return primes.toIntArray()
}
// 质数判断
private fun isPrime(num: Int): Boolean {
var x = 2
while (x * x <= num) {
if (num % x == 0) return false
x++
}
return true
}
}
fun primeSubOperation(nums: IntArray): Boolean {
for (index in nums.size - 2 downTo 0) {
if (nums[index] < nums[index + 1]) continue
// 二分查找:寻找严格小于 nums[index] 且减去后形成递增的最小质数
var left = 0
var right = primes.size - 1
while (left < right) {
val mid = (left + right) ushr 1
if (primes[mid] >= nums[index] || nums[index] - primes[mid] < nums[index + 1]) {
right = mid
} else {
left = mid + 1
}
}
if (primes[left] >= nums[index] || nums[index] - primes[left] >= nums[index + 1]) return false
nums[index] -= primes[left]
}
return true
}
}
复杂度分析:
- 时间复杂度:$O(U·\sqrt{U} + nlgU)$ 其中 $n$ 是 $nums$ 数组的长度,$U$ 是输入数据范围,$U$ 为常数 $1000$;
- 空间复杂度:$O(1)$ 忽略预处理质数空间,仅使用常数级别空间。
题解二(Eratosthenes 埃氏筛 + 二分查找)
计算质数的部分可以用经典埃氏筛。
筛法求质数的思路是:如果 x 是质数,那么 x 的整数倍 2x、3x 一定不是质数。我们设 isPrime[i] 表示 i 是否为质数,从小开始遍历,如果 i 是质数,则同时将所有倍数标记为合数。事实上,我们不必从 x 开始标记,而是直接从 x*x 开始标记,因为 x * 2, x * 3 已经在之前被标记过,会重复标记。
class Solution {
companion object {
// 1000 以内的质数列表
private val primes = getPrimes(1000)
// 埃氏筛求质数
private fun getPrimes(max: Int): IntArray {
val primes = LinkedList<Int>()
val isPrime = BooleanArray(max + 1) { true }
for (num in 2..max) {
// 检查是否为质数,这里不需要调用 isPrime() 函数判断是否质数,因为它没被小于它的数标记过,那么一定不是合数
if (!isPrime[num]) continue
primes.add(num)
// 标记
var x = num * num
while (x <= max) {
isPrime[x] = false
x += num
}
}
return primes.toIntArray()
}
}
fun primeSubOperation(nums: IntArray): Boolean {
val n = nums.size
if (n <= 1) return true
for (index in n - 2 downTo 0) {
if (nums[index] < nums[index + 1]) continue
// 二分查找
var left = 0
var right = primes.size - 1
while (left < right) {
val mid = (left + right) ushr 1
if (primes[mid] >= nums[index] || nums[index] - primes[mid] < nums[index + 1]) {
right = mid
} else {
left = mid + 1
}
}
if (primes[left] >= nums[index] || nums[index] - primes[left] >= nums[index + 1]) return false
nums[index] -= primes[left]
}
return true
}
}
复杂度分析:
- 时间复杂度:$O(U·lgU + nlgU)$ 其中 $n$ 是 $nums$ 数组的长度,$U$ 是输入数据范围,$U$ 为常数 $1000$;
- 空间复杂度:$O(1)$ 忽略预处理质数空间,仅使用常数级别空间。
题解三(Euler 欧氏线性筛 + 二分查找)
尽管我们从 x * x 开始标记来减少重复标记,但 Eratosthenes 筛选法还是会重复标记一个合数。举个例子,400 这个数不仅会被 2 标记一遍,还会被 5 标记,这就导致了大量的重复计算。
为了避免重复标记,我们使用欧氏筛,它与埃氏筛不同的是:
- 标记过程不再仅对质数 prime 标记,而是对每个数 x 标记;
- 不再标记所有 x* x 的整数倍,而是标记 x 与 “小于等于 x 的最小质因子的质数” 的乘积,保证每个合数只被标记最小的质因子标记。
class Solution {
companion object {
// 1000 以内的质数列表
private val primes = getPrimes(1000)
// 线性筛求质数
private fun getPrimes(max: Int): IntArray {
val primes = LinkedList<Int>()
val isPrime = BooleanArray(max + 1) { true }
for (num in 2..max) {
// 检查是否为质数,这里不需要调用 isPrime() 函数判断是否质数,因为它没被小于它的数标记过,那么一定不是合数
if (isPrime[num]) {
primes.add(num)
}
// 标记
for (prime in primes) {
if (num * prime > max) break
isPrime[num * prime] = false
if (num % prime == 0) break
}
}
return primes.toIntArray()
}
}
fun primeSubOperation(nums: IntArray): Boolean {
val n = nums.size
if (n <= 1) return true
for (index in n - 2 downTo 0) {
if (nums[index] < nums[index + 1]) continue
// 二分查找
var left = 0
var right = primes.size - 1
while (left < right) {
val mid = (left + right) ushr 1
if (primes[mid] >= nums[index] || nums[index] - primes[mid] < nums[index + 1]) {
right = mid
} else {
left = mid + 1
}
}
if (primes[left] >= nums[index] || nums[index] - primes[left] >= nums[index + 1]) return false
nums[index] -= primes[left]
}
return true
}
}
复杂度分析:
- 时间复杂度:$O(U + nlgU)$ 其中 $n$ 是 $nums$ 数组的长度,$U$ 是输入数据范围,$U$ 为常数 $1000$;
- 空间复杂度:$O(1)$ 忽略预处理质数空间,仅使用常数级别空间。
相似题目:
2601. 使数组元素全部相等的最少操作次数(Medium)
题目地址
https://leetcode.cn/problems/minimum-operations-to-make-all-array-elements-equal
题目描述
给你一个正整数数组 nums 。
同时给你一个长度为 m 的整数数组 queries 。第 i 个查询中,你需要将 nums 中所有元素变成 queries[i] 。你可以执行以下操作 任意 次:
- 将数组里一个元素 增大 或者 减小
1。
请你返回一个长度为 m 的数组 **answer ,其中 **answer[i]是将 nums 中所有元素变成 queries[i] 的 最少 操作次数。
注意,每次查询后,数组变回最开始的值。

题解(前缀和 + 二分查找)
一道题很明显有前缀和问题,难点也正是如何把原问题转换为前缀和问题。
如果用暴力解法,我们只需要计算每个元素到 queries[i] 的绝对值之和,单词查询操作的时间复杂度是 O(n),我们不考虑。
为了优化时间复杂度,我们分析数据的特征:
以 nums = [3,1,6,8], query = 5 为例,小于 5 的 3 和 1 需要增大才能变为 5,大于 5 的 6 和 8 需要减小才能变为 5。因此我们尝试将数组分为两部分 [3,1, | 6,8],需要执行加法的次数为 [+2,+4, | -1,-3]。
然而,我们不需要累加这 n 个差值的绝对值,而是使用前缀和在 O(1) 时间内快速计算。如图所示,小于 5 的部分可以用 “小于 5 的数字个数 _ 5” - “小于 5 的数字之和” 获得,大于 5 的部分可以用 “大于 5 的数字之和” - “大于 5 的数字个数 _ 5” 计算:
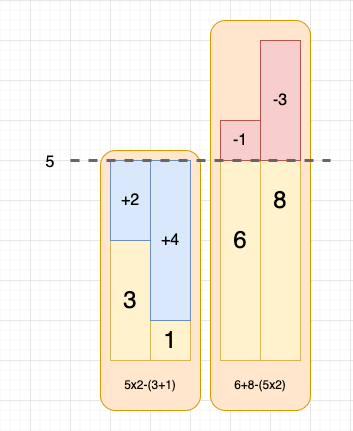
而 “小于 5 的数字之和” 与 “大于 5 的数字之和” 是明显的区间求和,可以用前缀和数组在 O(1) 时间复杂度解决。至此,我们成功将原问题转换为前缀和问题。
那么,剩下的问题是如何将数组拆分为两部分?
我们发现对于单次查询来说,我们可以使用快速选择算法在 O(lgn) 时间内找到。但是题目不仅只有一次,所以我们可以先对整个数组排序,再用二分查找找到枚举的分割点。
最后一个细节,由于数组的输入范围很大,所以前缀和数组要定义为 long 数组类型。
class Solution {
fun minOperations(nums: IntArray, queries: IntArray): List<Long> {
val n = nums.size
// 排序
nums.sort()
// 前缀和
val preSums = LongArray(n + 1)
for (index in nums.indices) {
preSums[index + 1] = nums[index] + preSums[index]
}
val ret = LinkedList<Long>()
for (target in queries) {
// 二分查找寻找大于等于 target 的第一个元素
var left = 0
var right = n - 1
while (left < right) {
val mid = (left + right) ushr 1
if (nums[mid] < target) {
left = mid + 1
} else {
right = mid
}
}
val index = if (nums[left] >= target) left - 1 else left
val leftSum = 1L * (index + 1) * target - preSums[index + 1]
val rightSum = preSums[n] - preSums[index + 1] - 1L * (n - 1 - index) * target
ret.add(leftSum + rightSum)
}
return ret
}
}
复杂度分析:
- 时间复杂度:$O(nlgn + qlgn)$ 其中 $n$ 是 $nums$ 数组的长度,$q$ 是 $queries$ 数组的长度。总共会执行 $q$ 次查询操作,每次查询操作的时间复杂度是 $O(lgn)$;
- 空间复杂度:$O(n)$ 前缀和数组空间。
近期周赛前缀和问题:
2602. 收集树中金币(Hard)
题目地址
https://leetcode.cn/problems/collect-coins-in-a-tree/
题目描述
给你一个 n 个节点的无向无根树,节点编号从 0 到 n - 1 。给你整数 n 和一个长度为 n - 1 的二维整数数组 edges ,其中 edges[i] = [ai, bi] 表示树中节点 ai 和 bi 之间有一条边。再给你一个长度为 n 的数组 coins ,其中 coins[i] 可能为 0 也可能为 1 ,1 表示节点 i 处有一个金币。
一开始,你需要选择树中任意一个节点出发。你可以执行下述操作任意次:
- 收集距离当前节点距离为
2以内的所有金币,或者 - 移动到树中一个相邻节点。
你需要收集树中所有的金币,并且回到出发节点,请你返回最少经过的边数。
如果你多次经过一条边,每一次经过都会给答案加一。
预备知识
- 拓扑排序:
给定一个包含 n 个节点的有向图 G,我们给出它的节点编号的一种排列,如果满足: 对于图 G 中的任意一条有向边 (u,v),u 在排列中都出现在 v 的前面。 那么称该排列是图 G 的「拓扑排序」。
- 拓扑排序的实现思路:
拓扑排序的常规实现是 Kahn 拓扑排序算法,基于 BFS 搜索和贪心思想:每次从图中删除没有前驱的节点(入度为 0),并修改它指向的节点的入度,直到 BFS 队列为空结束。
题解(拓扑排序 + 模拟)
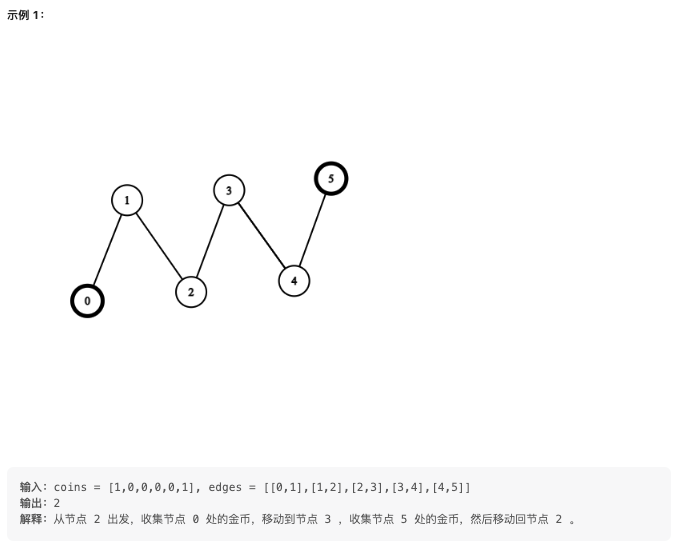
- 观察示例 1:从节点 2 出发,收集节点 0 处的金币,移动到节点 3 ,收集节点 5 处的金币,然后移动回节点 2。
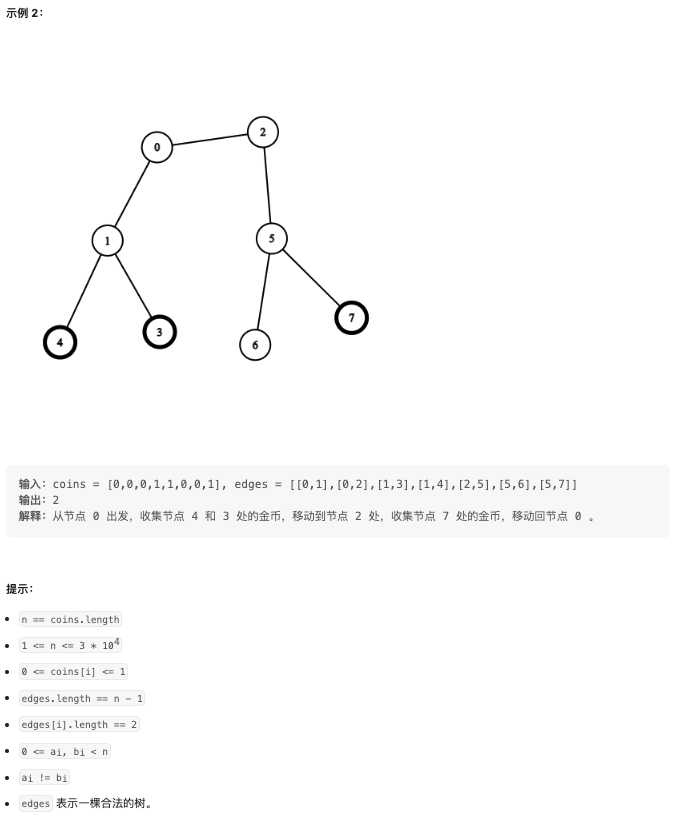
- 观察示例 2:从节点 0 出发,收集节点 4 和 3 处的金币,移动到节点 2 处,收集节点 7 处的金币,移动回节点 0。
结合题目规则(收集距离当前节点距离为 2 以内的所有金币)和这 2 个示例分析: 最优路径必然不需要触达图的边缘,而只需要在图的核心部分来回试探 (如示例 1 的节点 2 和节点 3,示例 2 的节点 0 和节点 2)。
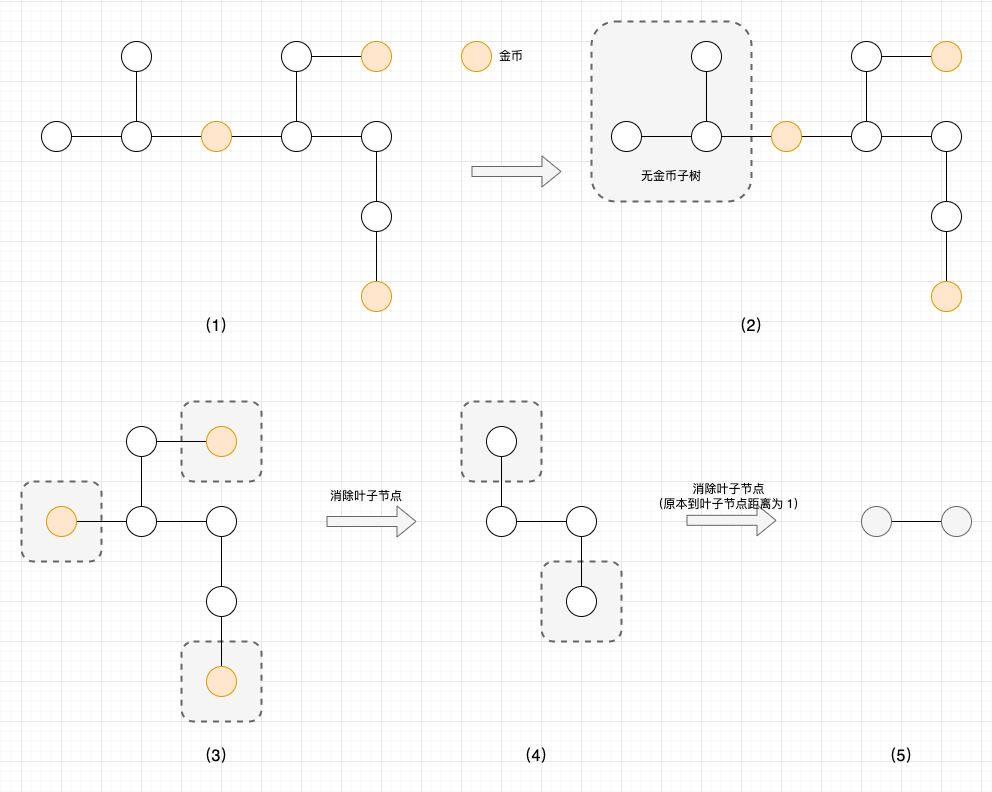
- 1、访问无金币的子树没有意义,我们将整个子树剪枝;
- 2、叶子节点和距离叶子节点距离为 1 的节点都没有必要访问,我们将这些点剪枝;
剩下的点就是必须经过的核心点。再结合题目规则(你需要收集树中所有的金币,并且回到出发节点),且题目保证输入数据是合法的树,因此答案正好就是剩下部分边的数目 * 2。
class Solution {
fun collectTheCoins(coins: IntArray, edges: Array<IntArray>): Int {
val n = coins.size
// 入度表
val inDegrees = IntArray(n)
// 领接表
val graph = HashMap<Int, MutableList<Int>>()
for (edge in edges) {
graph.getOrPut(edge[0]) { LinkedList<Int>() }.add(edge[1])
graph.getOrPut(edge[1]) { LinkedList<Int>() }.add(edge[0])
inDegrees[edge[0]]++
inDegrees[edge[1]]++
}
// 剩余的边
var left_edge = edges.size // n - 1
// 1、拓扑排序剪枝无金币子树
val queue = LinkedList<Int>()
for (node in 0 until n) {
// 题目是无向图,所以叶子结点的入度也是 1
if (inDegrees[node] == 1 && coins[node] == 0) {
queue.offer(node)
}
}
while (!queue.isEmpty()) {
// 删除叶子结点
val node = queue.poll()
left_edge -= 1
// 修改相邻节点
for (edge in graph[node]!!) {
if (--inDegrees[edge] == 1 && coins[edge] == 0) queue.offer(edge)
}
}
// 2、拓扑排序剪枝与叶子结点距离不大于 2 的节点(裁剪 2 层)
// 叶子节点
for (node in 0 until n) {
if (inDegrees[node] == 1 && coins[node] == 1) {
queue.offer(node)
}
}
for (node in queue) {
// 2.1 删除叶子结点
left_edge -= 1
// 2.2 删除到叶子结点距离为 1 的节点
for (edge in graph[node]!!) {
if (--inDegrees[edge] == 1) left_edge -= 1
}
}
// println(inDegrees.joinToString())
// coins=[0,0],edges=[[0,1]] 会减去所有节点导致出现负数
return Math.max(left_edge * 2, 0)
}
}
复杂度分析:
- 时间复杂度:$O(n)$ 其中 $n$ 是 $coins$ 数组的长度;
- 空间复杂度:$O(n)$。
相似题目:
有用请支持,你们的支持是我持续分享有价值内容的动力。
标签:周赛,埃氏,338,index,质数,nums,复杂度,primes,节点 From: https://www.cnblogs.com/pengxurui/p/17261219.html