1 前言
计算机中浮点数的编码,由美国加州大学的 William Kahan 教授于 1985 年设计,后被 IEEE 借鉴,制定出 IEEE 浮点标准。
浮点数在计算机中的二进制编码由符号位(S)、阶码(或指数 E)、尾数(或基数 M)组成。单精度浮点数组成:1S + 8E + 23M,双精度浮点数组成:1S + 11E + 52M.
通过如下方式可以打印浮点数的二进制编码:
System.out.println(Integer.toBinaryString(Float.floatToIntBits(f)));
System.out.println(Integer.toBinaryString(Double.doubleToLongBits(d)));
使用在线进制转换器工具,可以快速进行10进制与2进制的转换。
2 思考
在介绍浮点数存储原理之前,先列举几个 “神奇” 的案例。
//案例 1
System.out.println((123456725f - 3f > 123456724f)); // true
System.out.println((123456728f - 3f > 123456720f)); // true
//案例 2
System.out.println((123456724f + 4f < 123456725f)); // true
System.out.println((123456720f + 4f < 123456728f)); // true
//案例 3
int n = 123456789;
float s = 0f;
for (int i = 0; i < n; i++) {
s += 1f;
}
System.out.println(s); // 16777216
经常说不要使用浮点数进行 “==” 运算,但是案例 1 和案例 2 中,“>” 和 “<” 运算都出错了,案例 3 中最普通的累加运算也出错了,这使人怀疑,浮点数靠谱么?在了解浮点数的编码原理后,在一定的范围内使用浮点数,还是靠谱的。
3 编码原理
浮点数在计算机中的二进制编码由符号位(S)、阶码(或指数 E)、尾数(或基数 M)组成。单精度浮点数组成:1S + 8E + 23M,双精度浮点数组成:1S + 11E + 52M.
单精度浮点数
双精度浮点数
- 符号位(S):用于区分正数和负数,0 表示正数,1 表述负数。
- 阶码(E):十进制数转换为二进制数后,向左移动小数点到第一个1之后,记移动位数为 x(负数表示向右移动的位数),记阶码中间数为 m(8位阶码的中间数为127,11位阶码的中间数为1023),令 e = x + m,则 e 的二进制码即为阶码 E。
- 尾数(M):十进制数转换为二进制数后,向左(或向右)移动小数点到第一个1之后,则小数点之后的二进制码即为尾数 M(不包含第一个1)。
十进制数 d 与编码后的二进制浮点数中 S、E、M 的函数关系如下:
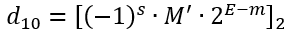
其中,M' 为 M 前面补上 “1.” 之后的二进制数,m 为阶码中间数的二进制编码,8位阶码的中间数为127,11位阶码的中间数为1023。
例:123.456 的浮点数编码过程如下:
// 1.符号位
123.456为正数,符号位为0
S = 0
// 2.阶码
123.456的二进制码为:1111011.0111010010111100011010101
小数点移到第一个1之后,需要向左移动6位
6 + 127 = 133
133对应的二进制为:10000101
E = 10000101
// 3.尾数
1111011.0111010010111100011010101的小数点向左移动6位:1.1110110111010010111100011010101
去掉前面的"1.",剩下:1110110111010010111100011010101
M = 1110110111010010111100011010101
// 4.浮点数编码
S E M
0 10000101 1110110111010010111100011010101
// System.out.println("0" + Integer.toBinaryString(Float.floatToIntBits(123.456f)));
4 最值问题
对于单精度浮点数,最大值、最小值、最小正数分别为:
// 1.最大数
// System.out.println("0" + Integer.toBinaryString(Float.floatToIntBits(Float.MAX_VALUE)));
浮点数编码:0 11111110 11111111111111111111111
十进制数:1.9999998807907104 * (2 ^ 127) = 3.4028235E38
// 2.最小数
// System.out.println(Integer.toBinaryString(Float.floatToIntBits(-Float.MAX_VALUE)));
浮点数编码:1 11111111 11111111111111111111111
十进制数:-1.9999998807907104 * (2 ^ 127) = -3.4028235E38
// 3.最小正数
// System.out.println("0000000000000000000000000000000" + Integer.toBinaryString(Float.floatToIntBits(Float.MIN_VALUE)));
浮点数编码:0 00000000 00000000000000000000001
十进制数:1.0000001192092896 * (2 ^ (-127)) = 1.4E-45
说明:“^” 表示幂运算。
5 精度问题
5.1 精度丢失原因
float 32 和 int 32 都是用 32 位二进制数表示,能表达的信息量应该一样多,即能映射的数字个数应该一样多。但是,float 32 能表示的最小值和最大值分别为 -3.4028235E38、3.4028235E38,int 32 能表示的最小值和最大值分别为 -2147483648、2147483647,float 32 的表示范围明显比 int 32 大,因此 float 32 必定会有精度损失,某些整数或小数不能映射到。
对于单精度浮点数,令尾数 M 表示如下:
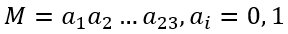
令 M' = 1.M,即
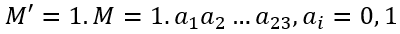
令 e = E - 127,则 e 表示 M' 的小数点需要向右(负数表示向左)移动的位数。
下面将根据 e 的取值范围讨论单精度浮点数的精度问题,为简化研究,下文只讨论正数,即 S = 0 的情况。
(1)0 <= e <= 23
在此范围内,[M' * 2 ^ e] 能表示的数可以用如下通式表示:
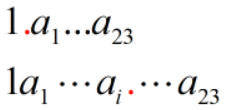
如果 a23 之后添加 1,就会造成小数精度丢失。
(2)-127 <= e < 0
在此范围内,[M' * 2 ^ e] 能表示的数可以用如下通式表示:
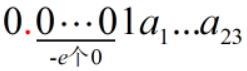
如果 a23 之后添加 1,就会造成小数精度丢失。
(3)23 < e < 127
在此范围内,[M' * 2 ^ e] 能表示的数可以用如下通式表示:
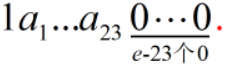
如果将 a23 之后的某些 0 改为 1,就会造成整数精度丢失;如果在小数点后添加 1,就会造成小数精度丢失。
5.2 刻度与有效位
(1)1为刻度的有效范围
通过第 2 节思考中案例 3,我们知道:16777216 + 1 不能进位到下一个整数,因此 1 不能作为 [-3.4028235E38, 3.4028235E38] 范围内整数的最小刻度,其有效范围是:[-16777216, 16777216]。
// 16777215 转换为二进制数:
System.out.println("0" + Integer.toBinaryString(Float.floatToIntBits(16777215f)));
浮点数编码:0 10010110 11111111111111111111111
二进制编码:111111111111111111111111 //24个1
// 16777216 转换为二进制数:
System.out.println("0" + Integer.toBinaryString(Float.floatToIntBits(16777216f)));
浮点数编码:0 10010111 00000000000000000000000
二进制编码:100000000000000000000000 //24个0
//16777216 的浮点数编码中尾数+1
浮点数编码:0 10010111 00000000000000000000001
二进制编码:1000000000000000000000010 //23个0
十进制数:16777218
由上述分析知,16777217 无法使用 32 位浮点数表示出来,因此 16777216f + 1 后还是 16777216f,即出现思考中的整数精度丢失现象。
同理,可求出双精度浮点数中,1 为刻度的整数有效范围是:[-2^53, 2^53],即 [-9007199254740992, 9007199254740992]
(2)十进制有效位数
单精度浮点数,二进制有效位为 23 位,有效位数为 6.92 位:
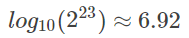
双精度浮点数,二进制有效位为 52 位,有效位数为 15.65 位:
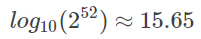
声明:本文转自浮点数编码原理
标签:编码,二进制,浮点数,System,println,原理,out From: https://www.cnblogs.com/zhyan8/p/17232795.html