数值积分原理与应用

1 理论

计算定积分时，可以通过微元法逼近，如下：

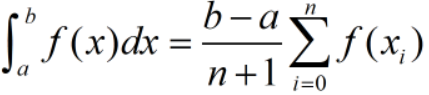
若取值均匀，公式如下：

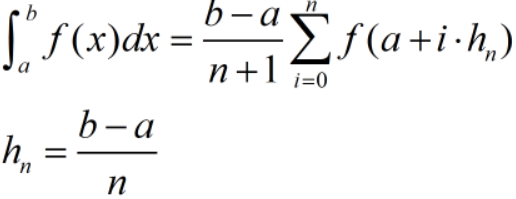
通过上述公式可以看到，定积分的值可以通过取样点函数值的线性组合得到。当取样点已经确定时，定积分的精度取决于每个取样点所分配的权值。梯形公式、Simpson公式、Cotes公式、Romberg公式正是通过调整权值来逐步逼近积分值。

（1）复合梯形公式

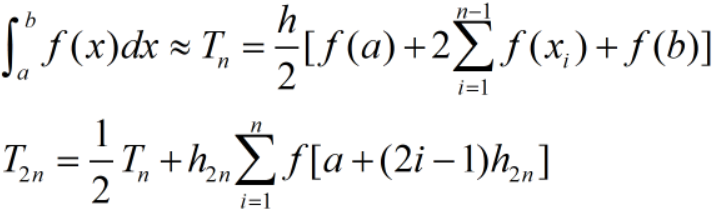
（2） Simpson公式

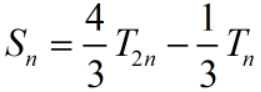
（3）Cotes公式

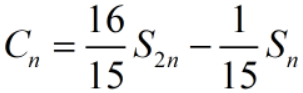
（4）Romberg公式

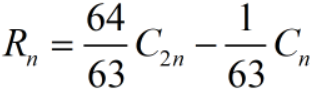
2 实验

借助如下公式，使用 Romberg 求积公式计算 π

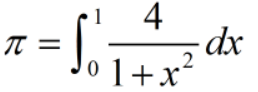
import numpy as np

def fun(x):
    return 4/(1+x*x)

def romberg(a,b,m): # m>=3
    p=np.zeros(m+1,dtype='int32') #p[i]=2**i
    p[0]=1;
    for i in range(1,m+1):
        p[i]=p[i-1]*2
    n=p[m]
    
    d=b-a
    f=np.random.uniform(a,b,n+1) #保存函数值
    for i in range(n+1):
        x=a+d/n*i
        f[i]=fun(x)
    print("f=\n",f)
    
    T=np.random.uniform(a,b,m) #保存梯度值
    T[0]=(f[0]+f[n])/2
    for i in range(1,m):
        s=0.0
        for k in np.arange(1,p[i-1]+1):
            s+=f[(2*k-1)*p[m-i]]
        T[i]=T[i-1]/2+d/p[i]*s
    print("T=\n",T)
    
    S=np.random.uniform(a,b,m-1) 
    for i in range(m-1):
        S[i]=(4*T[i+1]-T[i])/3 #Simpson公式
    print("S=\n",S)
    
    C=np.random.uniform(a,b,m-2) 
    for i in range(m-2):
        C[i]=(16*S[i+1]-S[i])/15 #Cotes公式
    print("C=\n",C)
    
    R=np.random.uniform(a,b,m-3) 
    for i in range(m-3):
        R[i]=(64*C[i+1]-C[i])/63 #Romberg公式
    print("R=\n",R)
    return R[-1]
    
s=romberg(0,1,8)

T=
 [3.         3.1        3.13117647 3.13898849 3.14094161 3.14142989
 3.14155196 3.14158248]
S=
 [3.13333333 3.14156863 3.1415925  3.14159265 3.14159265 3.14159265
 3.14159265]
C=
 [3.14211765 3.14159409 3.14159266 3.14159265 3.14159265 3.14159265]
R=
 [3.14158578 3.14159264 3.14159265 3.14159265 3.14159265]

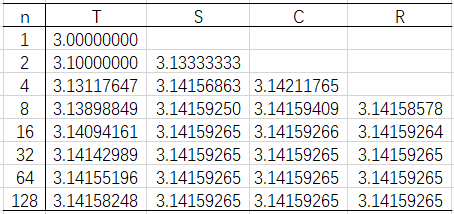
从运行结果可以看出，在取样点相同的情况下，梯形公式、Simpson公式、Cotes公式、Romberg公式的精度依次增加。

​ 声明：本文转自数值积分原理与应用