407. 接雨水 II (Hard)

问题描述

407. 接雨水 II (Hard)

给你一个 m x n
的矩阵，其中的值均为非负整数，代表二维高度图每个单元的高度，请计算图中形状最多能接多少体积的雨水。

示例 1:

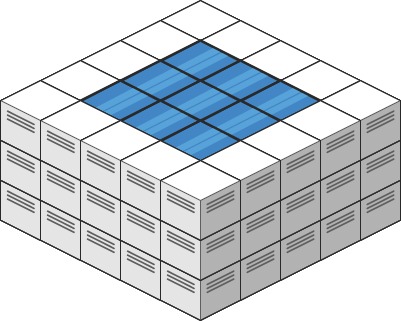
输入: heightMap = [[1,4,3,1,3,2],[3,2,1,3,2,4],[2,3,3,2,3,1]]
输出: 4
解释: 下雨后，雨水将会被上图蓝色的方块中。总的接雨水量为1+2+1=4。

示例 2:

输入: heightMap =
[[3,3,3,3,3],[3,2,2,2,3],[3,2,1,2,3],[3,2,2,2,3],[3,3,3,3,3]]
输出: 10

提示:

• m == heightMap.length
• n == heightMap[i].length
• 1 <= m, n <= 200
• 0 <= heightMap[i][j] <= 2 * 10⁴

解题思路

设方格\((i, j)\)到边界上的点\((x, y)\)的路径的最大高度为\(h_{x,y}\)，那么方格\((i, j)\)所能存放的雨水就是\(h_xy\)的最小值减去height[i][j]；

\(h_{x,y}\)也可以转化成边界上的点\((x, y)\)到方格\((i, j)\)的路径的上的方格的最大高度，那么就可以使用Dijkstra算法来解决，初始时将边界上所有的点都加入优先队列中，即可求边界上所有方格到\((i, j)\)的最大高度的最小值，还是使用小顶堆。

代码

class Solution {
  public:
    int trapRainWater(vector<vector<int>> &heightMap) {
        // 找边界上所有点，到x,y的路径上的最大高度的最小值（不包括x,y）
        // (x,y)处的存放的雨水即这个高度h-heightMap[x][y];
        int m = heightMap.size();
        int n = heightMap[0].size();
        auto cmp = [&](vector<int> &v1, vector<int> &v2) {
            return v1[2] > v2[2];
        };
        priority_queue<vector<int>, vector<vector<int>>, decltype(cmp)> pq(cmp);
        for (int i = 0; i < n; ++i) {
            pq.push({0, i, heightMap[0][i]});
            pq.push({m - 1, i, heightMap[m - 1][i]});
        }
        for (int i = 1; i < m - 1; ++i) {
            pq.push({i, 0, heightMap[i][0]});
            pq.push({i, n - 1, heightMap[i][n - 1]});
        }
        vector<vector<int>> dis(m, vector<int>(n));
        vector<vector<int>> vis(m, vector<int>(n));
        vector<vector<int>> neighbor{{-1, 0}, {1, 0}, {0, 1}, {0, -1}};
        while (!pq.empty()) {
            auto vec = pq.top();
            int x = vec[0], y = vec[1], height = vec[2];
            pq.pop();
            if (vis[x][y] != 0) {
                continue;
            }
            vis[x][y] = 1;
            dis[x][y] = height;
            for (int i = 0; i < 4; ++i) {
                int new_x = x + neighbor[i][0];
                int new_y = y + neighbor[i][1];
                if (new_x < m && new_x >= 0 && new_y < n && new_y >= 0) {
                    pq.push({new_x, new_y, std::max(height, heightMap[new_x][new_y])});
                }
            }
        }
        int res = 0;
        for (int i = 1; i < m - 1; ++i) {
            for (int j = 1; j < n - 1; ++j) {
                res += dis[i][j] - heightMap[i][j];
            }
        }
        return res;
    }
};