动态规划
从两个角度进行讲解
- 常用的DP模型
- 背包问题
- DP的不同类型
- 线性DP
- 区间DP
- 状态压缩DP
- 树形DP
- 计数类DP
- 数位统计DP
DP问题,通常从2方面来思考:状态表示和状态计算
状态表示
从2方面考虑
-
集合(某一个状态表示的是哪一种集合)
-
属性(这个状态存的是集合的什么属性)
一般属性有三种:集合的最大值,集合的最小值,集合中的元素个数
状态计算
状态转移方程,即集合的划分。比如对 f(i, j),考虑如何将其划分成若干个更小的子集合,而这些更小的子集合,又能划分为更更小的子集合。
集合的划分有2个原则:
- 不重:即不重复,某个元素不能既属于子集合A,又属于子集合B
- 不漏:即不漏掉任一元素,某个元素不能不属于任何一个子集合。
通常需要满足不漏原则,而不重不一定需要满足。
背包问题
什么是背包问题?
给定N个物品和一个容量为V的背包,每个物品有体积和价值两种属性,在一些限制条件下,将一些物品装入背包,使得在不超过背包体积的情况下,能够得到的最大价值。根据不同的限制条件,分为不同类型的背包问题。
0-1背包问题
给定\(N\)个物品,和一个容量为\(V\)的背包,每个物品有2个属性,分别是它的体积\(v_i\) (\(v\) for volume),和它的价值\(w_i\) (\(w\) for weight),每件物品只能使用一次(0-1背包的特点,每件物品要么用1次(放入背包),要么用0次(不放入背包)),问往背包里放入哪些物品,能够使得物品的总体积不超过背包的容量,且总价值最大。
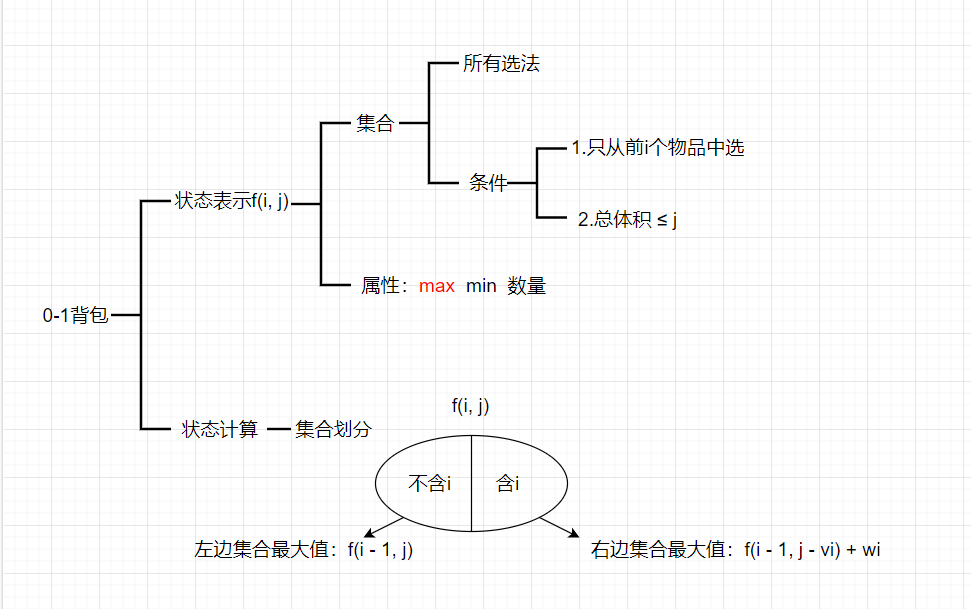
f(i, j)可以分成两个更小的集合,一种是不包含第i个物品,一种是包含第i个物品
- 不包含第i个物品:就是从物品
1-i中选择,但是不能包含第i个物品的最大价值,换句话就是从物品1-i-1中选择,总体积不超过j的最大价值,即f(i - 1, j) - 包含第i个物品:就是从物品
1-i中选择,但是必须包含第i个物品的最大价值,那么可以认为最开始直接把i塞进背包,此时背包的容量变成了j - vi,价值变成了wi,由于第i个物品已经装进背包了,那么从1-i选就变成了从1-i-1选了,因此此时的最大价值就是f(i - 1, j - vi) + wi
f(i, j)取两种情况的最大值,因此f(i, j)= max(f(i - 1, j), f(i - 1, j - vi) + wi)
模板问题 01背包问题
有 N 件物品和一个容量是 V 的背包。每件物品只能使用一次。
第 i 件物品的体积是 vi,价值是 wi。
求解将哪些物品装入背包,可使这些物品的总体积不超过背包容量,且总价值最大。输出最大价值。
输入格式
第一行两个整数,N,V,用空格隔开,分别表示物品数量和背包容积。
接下来有 N 行,每行两个整数 vi, wi,用空格隔开,分别表示第 i 件物品的体积和价值。
输出格式
输出一个整数,表示最大价值。
数据范围
0<N,V≤1000
0<vi,wi≤1000
朴素做法
#include<iostream>
#include<algorithm>
using namespace std;
const int N = 1010;
int v[N], w[N];
int f[N][N];
int main() {
int n, m;
cin >> n >> m;
for (int i = 1; i <= n; i++) cin >> v[i] >> w[i];
// 应该初始化f[0][0~m] = 0, 由于定义的是全局变量因此直接就是0
for (int i = 1; i <= n; i++) {
for (int j = 0; j <= m; j++) {
f[i][j] = f[i - 1][j];
if (j >= v[i]) f[i][j] = max(f[i][j], f[i - 1][j - v[i]] + w[i]);
}
}
cout << f[n][m] << endl;
return 0;
}
滚动数组优化
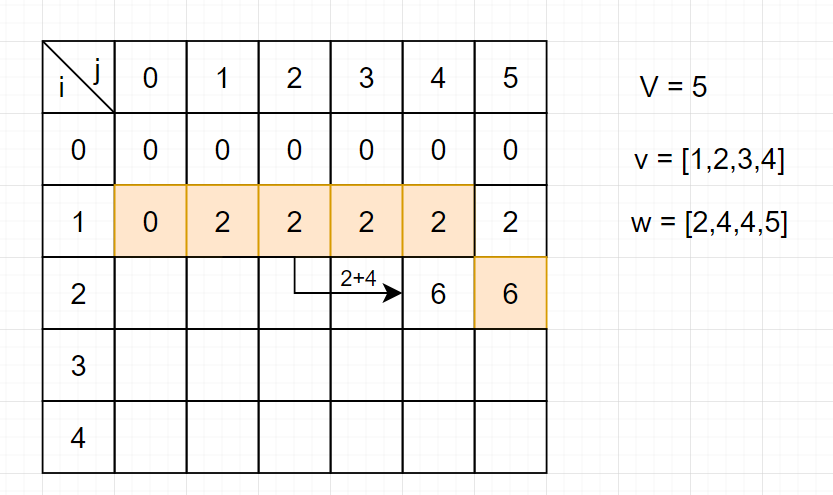
因为每次计算f[i][j]只会用到第i-1行的值,因此可以只用一个f[2][N]的数组存储两行,当我们采取倒序遍历时可以只存储一行,即用一维数组f[N]存储,为什么使用倒序遍历?
计算f[j]需要用到前一行的f[j - v[i]],因此不能提前更新f[j]之前的列,因此选择倒序遍历
#include<iostream>
#include<algorithm>
using namespace std;
const int N = 1010;
int v[N], w[N];
int f[N];
int main() {
int n, m;
cin >> n >> m;
for (int i = 1; i <= n; i++) cin >> v[i] >> w[i];
// 应该初始化f[0][0~m] = 0, 由于定义的是全局变量因此直接就是0
for (int i = 1; i <= n; i++) {
for (int j = m; j >= v[i]; j--) {
f[j] = max(f[j], f[j - v[i]] + w[i]);
}
}
cout << f[m] << endl;
return 0;
}
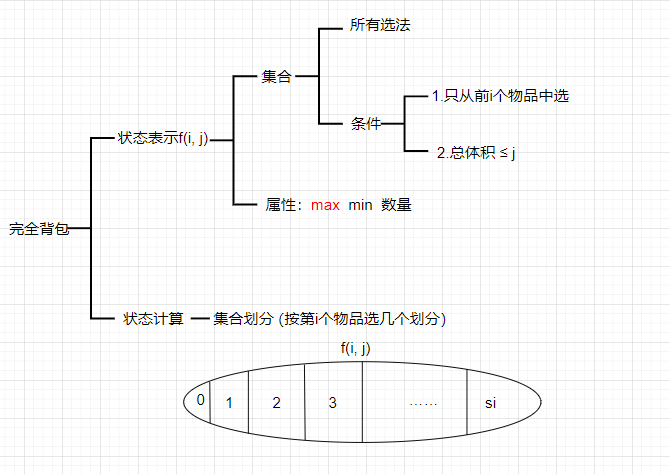
完全背包
定义与 0-1 背包类似,只是每件物品可以用无限次
模板问题 完全背包问题
有 N 种物品和一个容量是 V 的背包,每种物品都有无限件可用。
第 i 种物品的体积是 vi,价值是 wi。
求解将哪些物品装入背包,可使这些物品的总体积不超过背包容量,且总价值最大。输出最大价值。
输入格式
第一行两个整数,N,V,用空格隔开,分别表示物品种数和背包容积。
接下来有 N 行,每行两个整数 vi,wi,用空格隔开,分别表示第 i 种物品的体积和价值。
输出格式
输出一个整数,表示最大价值。
数据范围
0<N,V≤1000
0<vi,wi≤1000
朴素做法,时间复杂度最坏是\(O(N \times V^{2})\),会TLE
#include<iostream>
#include<algorithm>
using namespace std;
const int N = 1010;
int v[N], w[N];
int f[N][N];
int main() {
int n, m;
cin >> n >> m;
for (int i = 1; i <= n; i++) cin >> v[i] >> w[i];
for (int i = 1; i <= n; i++)
for (int j = 0; j <= m; j++)
for (int k = 0; k * v[i] <= j; k++)
f[i][j] = max(f[i][j], f[i - 1][j - v[i] * k] + w[i] * k);
cout << f[n][m] << endl;
return 0;
}
优化

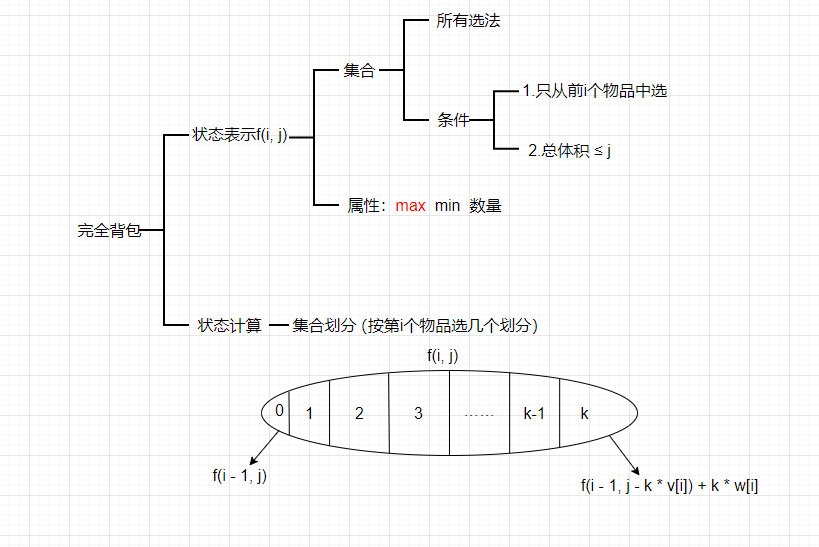
根据上图的推导过程,我们实际上可以用2个状态来推导出 f[i][j],即f[i][j]=max{f[i - 1][j],f[i][j − vi] + wi},此时f[i][j]的推导就和 k 无关了
理解:其实可以分成两种情况:
- 一个物品i都不选:就是从物品
1-i中选择,但是不能包含第i个物品的最大价值,换句话就是从物品1-i-1中选择,总体积不超过j的最大价值,即f(i - 1, j) - 至少选一个物品i:那就是最开始直接在背包里塞一个物品
i,此时背包容积变成j-vi,价值wi,那么再从1-i个物品中选择,且总体积不超过j-vi的最大价值(还选不选第i个物品不考虑,这是f(i, j-vi)该考虑的事情,只要f(i, j-vi)的最大值),总的最大价值就是f(i ,j-vi) + wi
f(i, j)取两种情况的最大值,因此f(i, j)= max(f(i - 1, j), f(i, j - vi) + wi)
#include<iostream>
#include<algorithm>
using namespace std;
const int N = 1010;
int v[N], w[N];
int f[N][N];
int main() {
int n, m;
cin >> n >> m;
for (int i = 1; i <= n; i++) cin >> v[i] >> w[i];
for (int i = 1; i <= n; i++)
for (int j = 0; j <= m; j++) {
f[i][j] = f[i - 1][j];
if (v[i] <= j) f[i][j] = max(f[i][j], f[i][j - v[i]] + w[i]);
}
cout << f[n][m] << endl;
return 0;
}
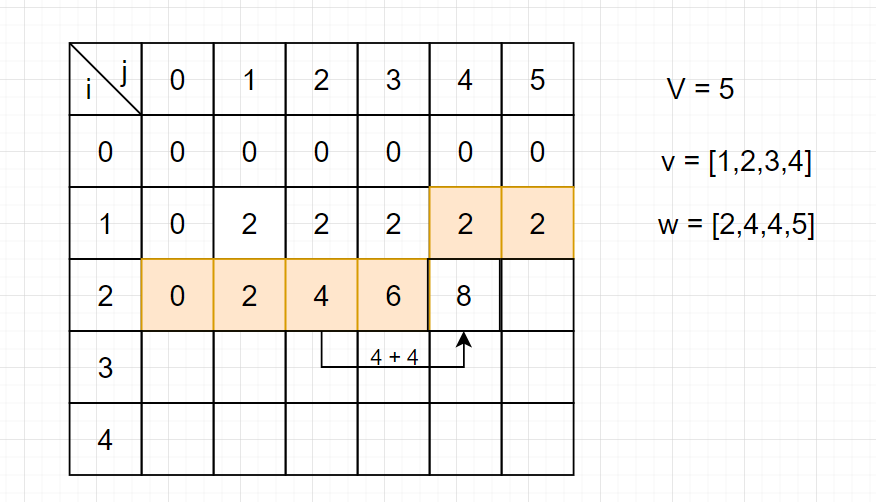
将二维数组通过滚动数组的思想,优化成一维数组,这跟01背包的优化略有不同,因为f(i,j)依赖于f(i,j-v[i]),依赖于本行,而不是上一行,所以j 的枚举要从小到大,保证在更新f(i,j)时,f(i,j−v[i]) 已经更新过了
#include<iostream>
#include<algorithm>
using namespace std;
const int N = 1010;
int v[N], w[N];
int f[N];
int main() {
int n, m;
cin >> n >> m;
for (int i = 1; i <= n; i++) cin >> v[i] >> w[i];
for (int i = 1; i <= n; i++)
for (int j = v[i]; j <= m; j++)
f[j] = max(f[j], f[j - v[i]] + w[i]);
cout << f[m] << endl;
return 0;
}
多重背包
每件物品的个数是不同的,比如,每件物品的个数是si个。
\(f(i,j)=max\{{f(i−1,j−v[i]×k)+k×v[i]}\}\), \(k \in [0,s[i]]\)
多重背包只是对每个物品,多了数量限制,而完全背包没有数量限制。
模板问题 多重背包问题 I
有 N 种物品和一个容量是 V 的背包。
第 i 种物品最多有 si 件,每件体积是 vi,价值是 wi。
求解将哪些物品装入背包,可使物品体积总和不超过背包容量,且价值总和最大。输出最大价值。
输入格式
第一行两个整数,N,V,用空格隔开,分别表示物品种数和背包容积。
接下来有 N 行,每行三个整数 vi, wi, si,用空格隔开,分别表示第 i 种物品的体积、价值和数量。
输出格式
输出一个整数,表示最大价值。
数据范围
0<N,V≤100
0<vi,wi,si≤100
朴素做法 时间复杂度最坏是\(O(N \times V \times S)\),数据范围小,因此可以AC
#include<iostream>
#include<algorithm>
using namespace std;
const int N = 110;
int v[N], w[N], s[N];
int f[N][N];
int main() {
int n, m;
cin >> n >> m;
for (int i = 1; i <= n; i++) cin >> v[i] >> w[i] >> s[i];
for (int i = 1; i <= n; i++)
for (int j = 0; j <= m; j++)
for (int k = 0; k <= s[i] && k * v[i] <= j; k++)
f[i][j] = max(f[i][j], f[i - 1][j - v[i] * k] + w[i] * k);
cout << f[n][m] << endl;
}
优化
首先,还是按照完全背包的优化思路,推导一下状态转移方程:(下面用 v来代表 v[i],w代表w[i],s代表s[i])
f[i,j] = max(f[i-1,j], f[i-1,j-v] + w, f[i-1,j-2v] + 2w ,..., f[i-1,j-sv] + sw)
f[i,j-v] = max( f[i-1,j-v], f[i-1,j-2v] + w ,..., f[i-1,j-sv] + (s-1)w + f[i-1,j-(s+1)v] + sw)
两个状态转移方程,只有中间一部分是相同的,无法进行替换。
个人理解,不能分成不选第i个物品,和至少选一个物品i两种情况,因为最开始强行往背包里塞一个物品i,那么可能最大的f(i, j - vi) 已经选了si个物品i,这个时候加上最开始塞的一个就超过了si限制,和完全背包不同,完全背包,不管f(i, j - vi) 选了几个物品i,加上最开始的一个也还是小于无穷
二进制优化\(O(N \times V \times logS)\)
考虑用一种二进制的方式,比如对于某个 i,其s[i]=1023,则对于该物品,一共需要枚举0,1,2,3,....,1023,共1024种情况。我们可以这样:只保留2的幂的数,然后其他数用2的幂来凑。
比如对0到1023,我们只保留1,2,4,8,16,...,512,共10个数字,则0到1023的任意数字,都能由这10个数字组合相加得到。(其实这个思想的本质就是把一个十进制的数,化成二进制表示)。这样以来,我们无需枚举0到1023,只需要枚举1,2,4,8,...,512这10个数即可 。
上面是恰好s[i]=1023 ,共枚举 \(2^{10}\)种情况,假设s[i]不是2的幂呢?比如s[i]=200,此时我们需要1,2,4,8,16,32,64,此时不能要128,因为加上128后,能凑出的数的范围就超过200了,而1,2,4,8,16,32,64能凑出的最大的数是127,和200还差73,所以我们补上一个数字73,即我们使用1,2,4,8,16,32,64,73就能凑出0到200内的任意一个数字了。
所以,对于物品i,共有s[i]个,其实我们可以把s[i]个物品,拆分成\(log_{2}s[i]\)个新的物品。然后对这些新的物品,做一次01背包问题即可。
#include<iostream>
using namespace std;
const int N = 25000;
int m, n;
int v[N], w[N];
int f[N];
int main() {
cin >> n >> m;
int cnt = 0;
for (int i = 0; i < n; i++) {
int a, b, s;
int k = 1;
cin >> a >> b >> s;
while (k <= s) {
cnt++;
v[cnt] = a * k;
w[cnt] = b * k;
s -= k;
k *= 2;
}
if (s > 0) {
cnt++;
v[cnt] = a * s;
w[cnt] = b * s;
}
}
n = cnt;
for (int i = 1; i <= n; i++)
for (int j = m; j >= v[i]; j--)
f[j] = max(f[j], f[j - v[i]] + w[i]);
cout << f[m] << endl;
return 0;
}
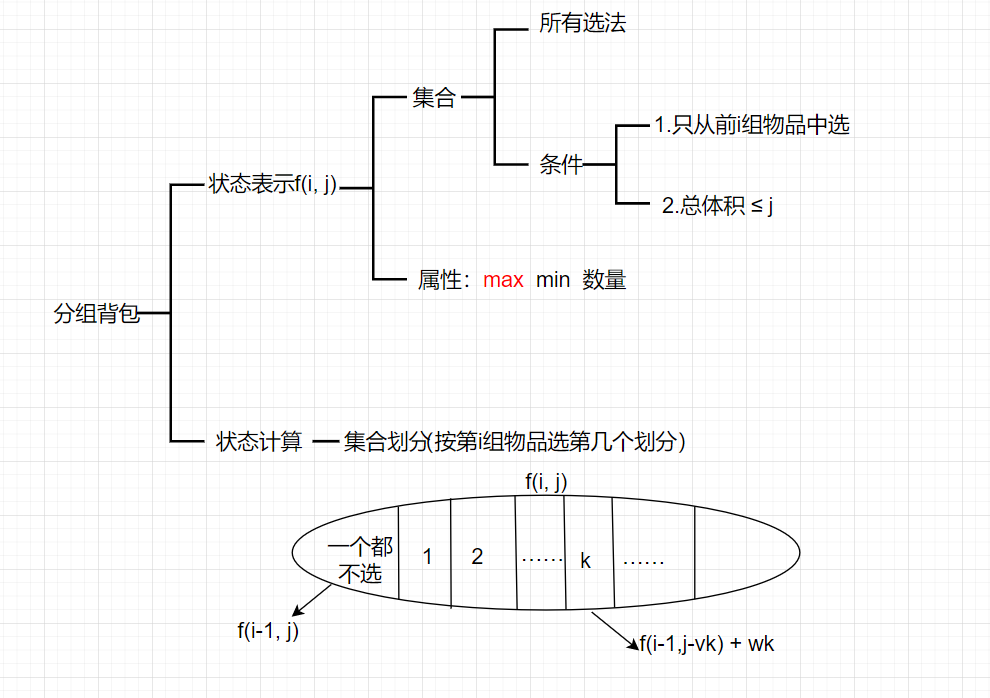
分组背包
有 N 组物品,每一组中有若干个物品,每一组中至多选择一个。
分组背包问题的思考方式和前面的类似。不同的地方仅仅在于状态转移。
01背包的状态转移,是枚举第i个物品选或者不选;
完全背包和多重背包,是枚举第i个物品,选0,1,2,3,4,.... 个
而分组背包,枚举的是第i个分组,选哪一个,或者不选
分组背包的状态转移方程为:
\(f(i,j)=max{\{f(i−1,j),f(i−1,j−v[i,k])+w[i,k]\}}\) , \(k \in [1,s[i]]\)
其中 v[i,k] 表示第 i 组中的第 k 个物品的体积,w [ i , k ] 同理
模板问题 分组背包问题
有 N 组物品和一个容量是 V 的背包。
每组物品有若干个,同一组内的物品最多只能选一个。每件物品的体积是 \(v_{ij}\),价值是 \(w_{ij}\),其中 i 是组号,j 是组内编号。
求解将哪些物品装入背包,可使物品总体积不超过背包容量,且总价值最大。
输出最大价值。
输入格式
第一行有两个整数 N,V,用空格隔开,分别表示物品组数和背包容量。
接下来有 N 组数据:
- 每组数据第一行有一个整数 \(S_i\),表示第 i个物品组的物品数量;
- 每组数据接下来有 \(S_i\)行,每行有两个整数 \(v_{ij}\),\(w_{ij}\),用空格隔开,分别表示第 i个物品组的第 j个物品的体积和价值;
输出格式
输出一个整数,表示最大价值。
数据范围
0<N,V≤100
0<\(S_i\)≤100
0<\(v_{ij}\),\(w_{ij}\)≤100
#include <iostream>
using namespace std;
const int N = 110;
int n, m;
int v[N][N], w[N][N], s[N];
int f[N];
int main() {
cin >> n >> m;
for(int i = 1; i <= n; i++) {
cin >> s[i];
for(int j = 0; j < s[i]; j++)
cin >> v[i][j] >> w[i][j];
}
for(int i = 1; i <= n; i++)
for(int j = m; j >= 0; j--)
for(int k = 0; k < s[i]; k++)
if(v[i][k] <= j)
f[j] = max(f[j], f[j - v[i][k]] + w[i][k]);
cout << f[m] << endl;
return 0;
}