G. Even Tree Split
题意:
给定一个节点数为偶数的树,请问有多少种方案使得切割开一条边使得剩余连通块的大小都是偶数。
分析:
我们发现断开一条边是独立的,因为如果两个连通块分开后都是偶数再断开仍然是偶数。因此我们只需要找到有多少个满足要求的边,再统计这个边选与不选即可。
如何判断该边是否满足要求呢?
先预处理出所有树的size,那么如果他的子树大小size是偶数,n也是偶数,上面部分也是偶数,说明这个边就是能够被分割的,暴力O(n)统计即可。
最后记得减去一个全都不选的情况。
void dfs(int u, int fa) {
siz[u] = 1;
for (int v : g[u]) {
if (v == fa)continue;
dfs(v, u);
siz[u] += siz[v];
}
}
void dfs1(int u, int fa) {
for (int v : g[u]) {
if (v == fa)continue;
if ((siz[v] % 2) == 0)tot++;
dfs1(v, u);
}
}
void slove() {
cin >> n;
for (int i = 1; i <= n; i++)g[i].clear();
for (int i = 1; i <= n - 1; i++) {
int u, v; cin >> u >> v;
g[u].push_back(v);
g[v].push_back(u);
}
tot = 0;
dfs(1, 0);
for (int i = 1; i <= n; i++)if (siz[i] % 2 == 0)tot++;
tot--;
cout << (ksm(2, tot, mod) - 1 + mod)%mod<< endl;
}
B. Wavy Tree
题意:
定义一个特殊数组a,使得除了两个端点之外,所有的点都小于相邻的两个边或者大于相邻两个边,给定一个数组,你可以修改一个数的大小,代价就是你修
改的量,请最小化代价使得该数组变成特殊数组。
分析:
只有“W” 和“M” 形状 所以只要将两种情况分别考虑即可
ll fun1() {
for (int i = 1; i <= n; i++)b[i] = d[i];
ll res = 0;
for (int i = 2; i <= n; i++) {
if (i % 2 == 0) {
// < 0
if (b[i] >= 0) {
res += (b[i] + 1);
b[i + 1] += (b[i] + 1);
b[i] = -1;
}
}
else {
// > 0
if (b[i] <= 0) {
res += (-b[i] + 1);
b[i + 1] -= (-b[i] + 1);
b[i] = 1;
}
}
}
return res;
}
ll fun2() {
for (int i = 1; i <= n; i++)b[i] = d[i];
ll res = 0;
for (int i = 2; i <= n; i++) {
if (i % 2 == 0) {
// > 0
if (b[i] <= 0) {
res += (-b[i] + 1);
b[i + 1] -= (-b[i] + 1);
b[i] = 1;
}
}
else {
// < 0
if (b[i] >= 0) {
res += (b[i] + 1);
b[i + 1] += (b[i] + 1);
b[i] = -1;
}
}
}
return res;
}
void slove() {
cin >> n;
for (int i = 1; i <= n; i++)cin >> a[i];
for (int i = 1; i <= n; i++)d[i] = a[i] - a[i - 1];
cout << min(fun1(), fun2()) << endl;
}
D. Average Replacement
题意:
有n人,其中有m对朋友关系。朋友的朋友并不算是朋友,现在,每个人的帽子上都有一个整数,每一轮游戏中,每个人帽子上的整数都会变成他
及其所有朋友的帽子上的整数的平均值,这个数可能不是整数,给定一个结论,当游戏次数足够多时,所有人的整数将会固定不变,求出这些最终值。
分析:
游戏轮次足够多时,容易想到同一个连通块里最终的值都是一样的
问题变为一个连通块最终的值为多少
结论为Σ(a[i]×(d[i]+1))/sz[x] 其中d[i]表示i节点的度数 sz[x]表示连通块x的大小
结论要大胆猜 怎么理解呢 a[i]被自己和朋友都算了一遍 类似期望概率里面的极限情况
#include<cstdio>
#include<iostream>
#include<algorithm>
#include<cstring>
#include<map>
#include<queue>
#include<vector>
#include<cmath>
using namespace std;
const int N=3e5+10;
int a[N],fu[N],d[N],sz[N];
long long sum[N];
int find(int x)
{
if(x!=fu[x]) return fu[x]=find(fu[x]);
return fu[x];
}
int main()
{
int T;
cin>>T;
while(T--)
{
int n,m;
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++)
{
scanf("%d",&a[i]);
sum[i]=d[i]=sz[i]=0;
fu[i]=i;
}
for(int i=1;i<=m;i++)
{
int u,v;
scanf("%d%d",&u,&v);
d[u]++;d[v]++;
int fx=find(u),fy=find(v);
if(fx!=fy) fu[fy]=fx;
}
for(int i=1;i<=n;i++)
{
sum[find(i)]+=1ll*a[i]*(d[i]+1);
sz[find(i)]+=d[i]+1;
}
for(int i=1;i<=n;i++)
printf("%.6lf\n",1.0*sum[find(i)]/sz[find(i)]);
}
return 0;
}
A. Winner Prediction
题意:
有 n 个人参与比赛,已知m场比赛的结果,但是还有k场比赛没有结束。最终获胜场数最多的人(可能是多个人)会获的奖品,你是 1 号选手的亲爹,并且你能
够暗箱操作后 k 场比赛的结果,请问能否让 1 号选手获得胜利。
分析:
和之前有道题很像 都是比较裸的网络流 https://www.cnblogs.com/wzxbeliever/p/16099938.html
首先暗箱操作k场比赛 使得有1 参与的都赢
对每场比赛建图
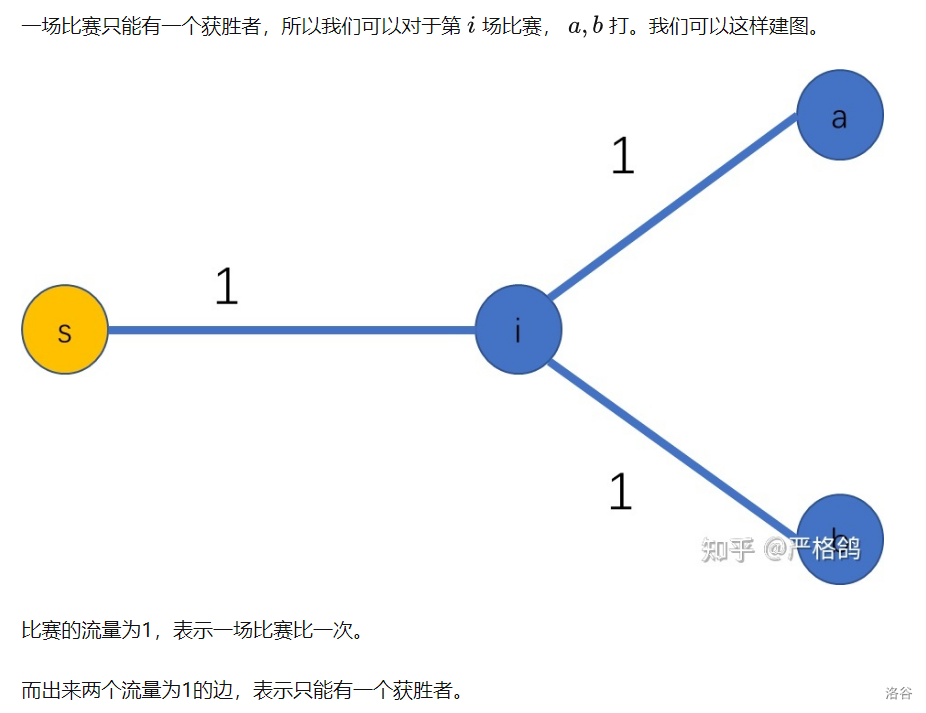
这样就完了嘛?万一有人胜场比1多就不成立
假如i号选手目前赢了b场,1号选手赢了a场,那么他能够最多还能赢a - b场。
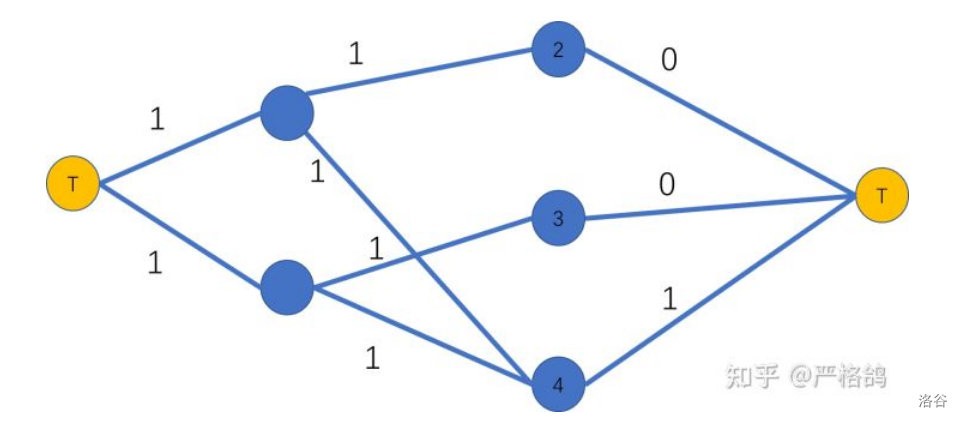
最终判断流向T节点的流的大小 如果与场数不符合即不成立
int n, m, S, T;
int idx;
int h[N], e[M], f[M], ne[M];
int d[N], cur[M];
void add(int a, int b, int w) {
e[idx] = b, f[idx] = w, ne[idx] = h[a], h[a] = idx++;
e[idx] = a, f[idx] = 0, ne[idx] = h[b], h[b] = idx++;
}
bool bfs() {
memset(d, -1, sizeof d);
queue<int> q;
q.push(S), d[S] = 0, cur[S] = h[S];
while (q.size()) {
auto u = q.front(); q.pop();
for (int i = h[u]; ~i; i = ne[i]) {
int v = e[i];
if (d[v] == -1 && f[i]) {
d[v] = d[u] + 1;
cur[v] = h[v];
if (v == T) return 1;
q.push(v);
}
}
}
return 0;
}
int found(int u, int limit) {
if (u == T) return limit;
int flow = 0;
for (int i = cur[u]; ~i && flow < limit; i = ne[i]) {
cur[u] = i;
int v = e[i];
if (d[v] == d[u] + 1 && f[i]) {
int t = found(v, min(f[i], limit - flow));
if (!t) d[v] = -1;
f[i] -= t, f[i ^ 1] += t, flow += t;
}
}
return flow;
}
int dinic() {
int res = 0, flow;
while (bfs()) {
while (flow = found(S, inf)) res += flow;
}
return res;
}
void init() {
memset(h, -1, sizeof h);
idx = 0;
}
void solve() {
init();
cin >> n;
int m1, m2; cin >> m1 >> m2;
S = 0, T = n + m2 + 1;
vector<int> a(n + 1);
int cnt = 0;
for (int i = 1; i <= m1; i++) {
int u, v, z; cin >> u >> v >> z;
if (z == 1) a[u]++;
else if (z == 0) a[v]++;
}
for (int i = 1; i <= m2; i++) {
int u, v; cin >> u >> v;
if (u == 1 || v == 1) cnt++;
else {
add(S, i, 1);
// cout << S << ' ' << cnt << endl;
add(i, m2 + u, 1);
add(i, m2 + v, 1);
}
}
int st = m2 - cnt;//还剩下几场比赛
cnt = cnt + a[1];
for (int i = 2; i <= n; i++) {
if (a[i] > cnt) {
cout << "NO" << endl;
return;
}
}
for (int i = m2 + 2; i <= m2 + n; i++) {
add(i, T, cnt - a[i - m2]);
}
int ans = dinic();
if (ans == st) cout << "YES" << endl;
else cout << "NO" << endl;
}
I. Painting Game
题意:
有一个长度为n的棋盘,Alice和Bob在棋盘上下棋,要求所有棋都不能相邻,每次告诉你棋盘长度和先手,Alice希望最后棋数量最少,Bob希望棋数量最多,
请问最终棋盘上会有多少棋。
分析:

此时会有疑问 为什么是n-4?不是分析的是三个格子嘛?
因为此时可能转移会有两个黑格子相邻的情况 所以不成立
但是如果bob转移变成n-4就能完全避免这种情况
原先的xox 变成了oxox
不得不说这个题很妙
标签:杭电多校,return,idx,10,int,void,flow,2022,include From: https://www.cnblogs.com/wzxbeliever/p/16705302.html