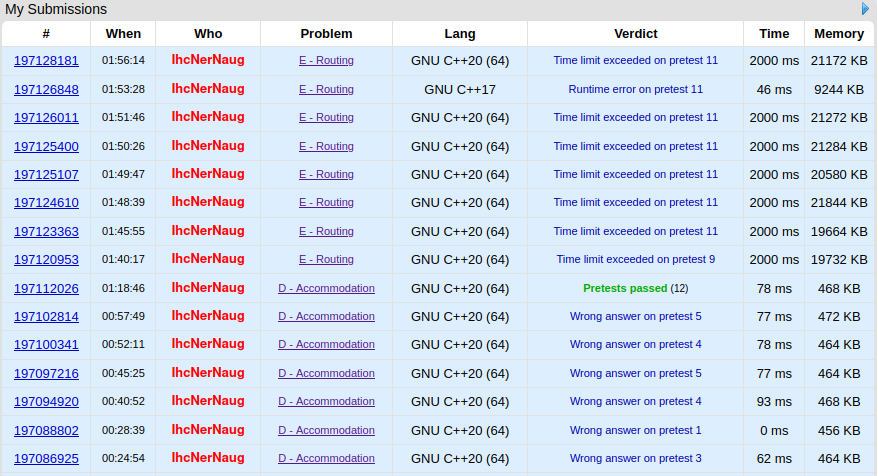
赛时战况,血压飙升,成功跳崖!
A
随便算一下就好了。
#include<bits/stdc++.h>
#define IL inline
#define reg register
IL int read()
{
reg int x=0; reg char ch=getchar();
while(ch<'0'||ch>'9')ch=getchar();
while(ch>='0'&&ch<='9')x=x*10+ch-'0',ch=getchar();
return x;
}
int n,m;
IL void work()
{
n=read(),m=read();
if(n<m)std::swap(n,m);
printf("%d\n",n+m+std::max(0,n-m-1));
}
main()
{
for(reg int t=read();t--;work());
}
B
直接从 \(1\) 到 \(n\) 枚举每个人,动态维护一下目前的药品用了多少与何时打开就好了。
#include<bits/stdc++.h>
#define IL inline
#define reg register
#define N 200200
IL int read()
{
reg int x=0; reg char ch=getchar();
while(ch<'0'||ch>'9')ch=getchar();
while(ch>='0'&&ch<='9')x=x*10+ch-'0',ch=getchar();
return x;
}
int n,k,d,w,x[N],ans;
IL void work()
{
n=read(),k=read(),d=read(),w=read();
for(reg int i=1;i<=n;++i)x[i]=read();
ans=0;
for(reg int i=1,s=0,t=-1e9;i<=n;++i)
if(s==k||x[i]-t>d)++ans,s=1,t=x[i]+w;
else ++s;
printf("%d\n",ans);
}
main()
{
for(reg int t=read();t--;work());
}
C
即找到最小的 \(m\) 使得 \(\frac{m(m+1)}{2}\equiv n-x(\text{mod}\ n)\),枚举 \(m=1\sim 2n\) 就好了。
#include<bits/stdc++.h>
#define IL inline
#define reg register
#define N 100100
IL int read()
{
reg int x=0; reg char ch=getchar();
while(ch<'0'||ch>'9')ch=getchar();
while(ch>='0'&&ch<='9')x=x*10+ch-'0',ch=getchar();
return x;
}
IL void cmin(reg int &x,reg int y){x>y?x=y:0;}
int n,x,p,f[N];
IL void work()
{
n=read(),x=read(),p=read();
for(reg int i=n;i--;)f[i]=2e9;
for(reg int i=1;i<=n+n;++i)cmin(f[1ll*i*(i+1)/2%n],i);
puts(f[(n-x)%n]<=p?"Yes":"No");
}
main()
{
for(reg int t=read();t--;work());
}
D
弱智贪心,但我更弱智,赛时这题做成那个鬼样子。
最小值与最大值,即使得两个窗口都是亮着的双卧公寓尽量多与尽量少。
前者每遇到一个连着的 \(1\) 就用一个双卧公寓,后者每遇到一个连着的,且不都是 \(1\) 就用一个。
#include<bits/stdc++.h>
#define IL inline
#define reg register
#define N 500500
IL int read()
{
reg int x=0; reg char ch=getchar();
while(ch<'0'||ch>'9')ch=getchar();
while(ch>='0'&&ch<='9')x=x*10+ch-'0',ch=getchar();
return x;
}
int n,m,ans_mn,ans_mx;
char s[N];
main()
{
n=read(),m=read();
while(n--)
{
scanf("%s",s+1);
reg int c0=0,c1=0,sum1=0;
for(reg int i=1;i<=m;++i)sum1+=s[i]=='1';
for(reg int i=1;i<m;++i)if(s[i]=='1'&&s[i+1]=='1')++i,++c0;
for(reg int i=1;i<m;++i)if(!(s[i]=='1'&&s[i+1]=='1'))++i,++c1;
c0=std::min(c0,m/4),c1=std::max(m/4-c1,0),ans_mn+=sum1-c0,ans_mx+=sum1-c1;
}
printf("%d %d\n",ans_mn,ans_mx);
}
E
考虑所有 \(u->a(u)\) 的连边,则连成了一个基环森林,容易发现只存在一个基环树时更优。
考虑枚举环上点,则可以简单判断有无解,并给出构造。
问题在于如何求出一个环,考虑状压。枚举环上最小点,破环为链,最小点为链头。记录 \(f(S)\) 表示目前环上点的集合是 \(S\),所有可能的链尾构成的集合。
转移是容易的,这样我们就可以求出所有点集不同的环,时间复杂度 \(O(n^22^n)\)。
这题赛时构造环的时候脑子短路了,想的和敲下去的不是一个东西,死循环了。
#pragma GCC optimize("inline")
#pragma GCC optimize("fast-math")
#pragma GCC optimize("Ofast,no-stack-protector,unroll-loops")
#pragma GCC target("sse,sse2,sse3,ssse3,sse4,sse4.1,sse4.2,popcnt,abm,mmx,avx,avx2,fma,tune=native")
#include<bits/stdc++.h>
#define IL inline
#define reg register
#define N 33
#define getchar()(inBuf==lenBuf?lenBuf=(inBuf=Buf)+fread(Buf,1,1<<20,stdin):0,inBuf==lenBuf?EOF:*inBuf++)
char Buf[1<<20],*inBuf,*lenBuf;
IL int read()
{
reg int x=0; reg char ch=getchar();
while(ch<'0'||ch>'9')ch=getchar();
while(ch>='0'&&ch<='9')x=x*10+ch-'0',ch=getchar();
return x;
}
int n,m,sta[N];
IL void add(reg int u,reg int v){sta[u-1]|=1<<v-1,sta[v-1]|=1<<u-1;}
int stk[N],ans[N],top,f[1<<20|5],id[1<<20|5];
IL void chk(reg int S)
{
for(reg int i=n,x;i--;)if(~S>>i&1)
{
x=sta[i]&S;
if(!x)return;
ans[i]=id[x&-x];
}
puts("Yes");
for(reg int i=1;i<top;++i)ans[stk[i]]=stk[i+1]; ans[stk[top]]=stk[1];
for(reg int i=0;i<n;++i)printf("%d%c",ans[i]+1," \n"[i==n-1]);
exit(0);
}
main()
{
n=read(),m=read(); while(m--)add(read(),read());
for(reg int i=n;i--;)id[1<<i]=i;
for(reg int i=0,s,j,S,k;i<n;++i)
{
for(s=1<<i;s<(1<<n);++s)f[s]=0; f[1<<i]=1<<i;
for(s=1<<i;s<(1<<n);++s)if(f[s])for(j=i;j<n;++j)if(~s>>j&1)
if((sta[j]&f[s])!=0)f[s|(1<<j)]|=1<<j;
for(s=1<<i;s<(1<<n);++s)if(f[s])for(j=i;j<n;++j)if((f[s]>>j&1)&&(sta[j]>>i&1))
{
stk[top=1]=k=j,S=s^(1<<k);
while(S)k=sta[k]&f[S],k=id[k&-k],stk[++top]=k,S^=1<<k;
chk(s); break;
}
}
puts("No");
}
F
这题好玩!但赛时我打得太重量级了,没做到这题。
注意到直接求图的直径没法做,但题目只要我们给出一个近似的直径就可以了。
可以想到求出 \(d'=\max_{i=1}^n dis(1,i)\),有 \(\lceil{\frac{d(G)}{2}}\rceil \le d' \le d(G)\),这 \(d'\) 就是一个“近似直径”。
直接每次都跑一遍 \(\texttt{bfs}\) 是 \(O(qm)\) 的,无法接受,考虑优化。
在不断地加边当中,直径会不断变小,\(d'\) 会在某个时刻 \(t\) 开始无法作为答案。那么在这个时刻,以求 \(d'\) 同样的方式求出的 \(d_t\) 有什么性质呢?
由于 \(d'>d(G_t)\times 2, d_t\le d(G_t)\),我们就可以得到 \(d'> d_t\times 2\)。换而言之,\(d'\) 在时刻 \(i\) 无法作为答案的必要不充分条件是 \(d'> d_i\times 2\)。
我们不断地二分找到第一个满足这个必要条件的位置,显然只会有 \(log_n\) 种 \(d'\),时间复杂度 \(O(nlog^2n)\)。
#include<bits/stdc++.h>
#define IL inline
#define reg register
#define N 100100
IL int read()
{
reg int x=0; reg char ch=getchar();
while(ch<'0'||ch>'9')ch=getchar();
while(ch>='0'&&ch<='9')x=x*10+ch-'0',ch=getchar();
return x;
}
int n,m,q;
struct Edge{int u,v;}e[N];
std::vector<int>G[N],init_G[N];
IL void add(reg int u,reg int v){G[u].push_back(v),G[v].push_back(u);}
int que[N],head,tail,dis[N];
IL void cmax(reg int &x,reg int y){x<y?x=y:0;}
IL int solve(reg int t)
{
for(reg int i=1;i<=n;++i)G[i]=init_G[i];
for(reg int i=1;i<=t;++i)add(e[i].u,e[i].v);
que[head=tail=1]=1;
for(reg int i=1;i<=n;++i)dis[i]=i==1?0:-1;
while(head<=tail)
{
reg int u=que[head++];
for(reg auto v:G[u])if(!~dis[v])dis[que[++tail]=v]=dis[u]+1;
}
reg int mx=0;
for(reg int i=1;i<=n;++i)cmax(mx,dis[i]);
return mx;
}
int now_dis,now_id,ans[N];
main()
{
n=read(),m=read(),q=read();
while(m--)add(read(),read());
for(reg int i=1;i<=n;++i)init_G[i]=G[i];
for(reg int i=1;i<=q;++i)e[i]={read(),read()};
while(now_id<=q)
{
now_dis=solve(now_id); reg int l=now_id+1,r=q,mid;
while(l<=r)if(solve(mid=l+r>>1)*2<now_dis)r=mid-1; else l=mid+1;
++r; for(reg int i=now_id;i<r;++i)ans[i]=now_dis; now_id=r;
}
for(reg int i=0;i<=q;++i)printf("%d%c",ans[i]," \n"[i==q]);
}
G
咕咕咕。
H
咕咕咕。
标签:ch,int,IL,笔记,解题,CF1804,getchar,reg,define From: https://www.cnblogs.com/Nesraychan/p/17210988.html