A - CAPS LOCK
#include <bits/stdc++.h>
using namespace std;
int32_t main() {
string s;
cin >> s;
for( auto i : s )
cout << char(i - 'a' + 'A');
return 0;
}
B - Yellow and Red Card
把红牌当成两张黄牌,对于操作 3 就是查看\(x\)是否有大于等于两张黄牌
#include <bits/stdc++.h>
using namespace std;
int32_t main() {
int n , q;
cin >> n >> q;
vector<int> a( n+1 , 0 );
for( int opt , x ; q ; q -- ){
cin >> opt >> x;
if( opt == 1 ){
a[x] ++;
}else if( opt == 2 ){
a[x] += 2;
}else{
cout << ( a[x] >= 2 ? "Yes\n" : "No\n");
}
}
return 0;
}
C - Four Variables
令\(AB=x,CD=y\)则\(x+y=N,y=N-x\),所以先\(O(n)\)枚举出\(x,y\)
然后在\(O(\sqrt{N})\)的枚举出\(A,B,C,D\),记构成\(x\)的方案数是\(p\),如果\(A=B\),\(p=p+1\),否则\(p=p+2\),同理计算出\(y\)的方案数\(q\)
答案是\(res\),如果\(x=y\),\(res=res+pq\),否则\(res=res+2pq\)
#include <bits/stdc++.h>
using namespace std;
#define int long long
int32_t main() {
int n , res = 0;
cin >> n;
for( int a = 1 , b = n-1 , x , y ; a <= b ; a ++ , b -- ){
x = y = 0;
for( int i = 1 ; i * i <= a ; i ++ ){
if( a % i ) continue;
x ++;
if( i != a / i ) x ++;
}
for( int i = 1 ; i * i <= b ; i ++ ){
if( b % i ) continue;
y ++;
if( i != b / i ) y ++;
}
res += x * y;
if( a != b ) res += x * y;
}
cout << res;
return 0;
}
D - Unicyclic Components
并查集维护联通块,判断联通块内点数的二倍是否等于联通块内点度数之和
#include <bits/stdc++.h>
using namespace std;
int read(){
int x = 0 , f = 1 , ch = getchar();
while( (ch < '0' || ch > '9') && ch != '-' ) ch = getchar();
if( ch == '-' ) f = -1 , ch = getchar();
while( ch >= '0' && ch <= '9' ) x = ( x << 3 ) + ( x << 1 ) + ch - '0' , ch = getchar();
return x * f;
}
class dsu{
private:
vector<int> fa;
public:
dsu( int n = 1 ){
fa = vector<int>( n+1 , -1 ) , fa[0] = 0;
}
int getfa( int x ){
if( fa[x] < 0 ) return x;
return fa[x] = getfa( fa[x] );
}
void merge( int x , int y ){
x = getfa(x) , y = getfa(y);
if( x == y ) return ;
if( fa[x] > fa[y] ) swap( x , y );
fa[x] += fa[y] , fa[y] = x;
}
bool check( int x , int y ){
x = getfa(x) , y = getfa(y);
return ( x == y );
}
int size( int x ){
x = getfa(x);
return -fa[x];
}
};
int32_t main() {
int n = read() , m = read();
vector<int> e(n+1);
dsu d(n);
for( int u , v ; m ; m -- ){
u = read() , v = read();
d.merge( u , v );
e[u] ++ , e[v] ++;
}
map<int,int>cnt;
for( int i = 1 , t; i <= n ; i ++ )
t = d.getfa(i) , cnt[t] += e[i];
for( auto [k,v] : cnt )
if( v != d.size(k) * 2 ) return cout << "No\n" , 0;
cout << "Yes\n";
return 0;
}
E - Transitivity
对每一个点都进行 bfs,统计每一个点可以到达的所有的点。复杂度\(O(n^2)\)
#include<bits/stdc++.h>
using namespace std;
int32_t main() {
int n , m , cnt;
cin >> n >> m , cnt = -m;
vector<vector<int>> e(n);
for( int u, v; m; m -- )
cin >> u >> v, u --, v --, e[u].emplace_back(v);
for( int i = 0; i < n; i ++ ){
vector<bool> vis(n,false);
vis[i] = true;
queue<int> q;
q.push(i);
while( !q.empty() ){
auto u = q.front(); q.pop();
for( auto v : e[u] )
if( vis[v] == false )
vis[v] = true, q.push(v), cnt ++;
}
}
cout << cnt;
}
F - Regular Triangle Inside a Rectangle
首先保证\(A<B\),现在有两种情况
情况一是三角形的一条边和B重合此时答案就是\(r=\frac{A}{\sin\frac{\pi}{3}}\),条件是\(A\le B\sin\frac{\pi}{3}\)
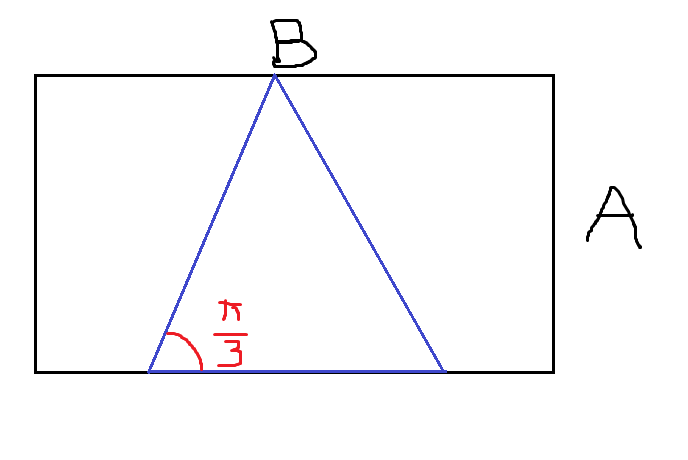
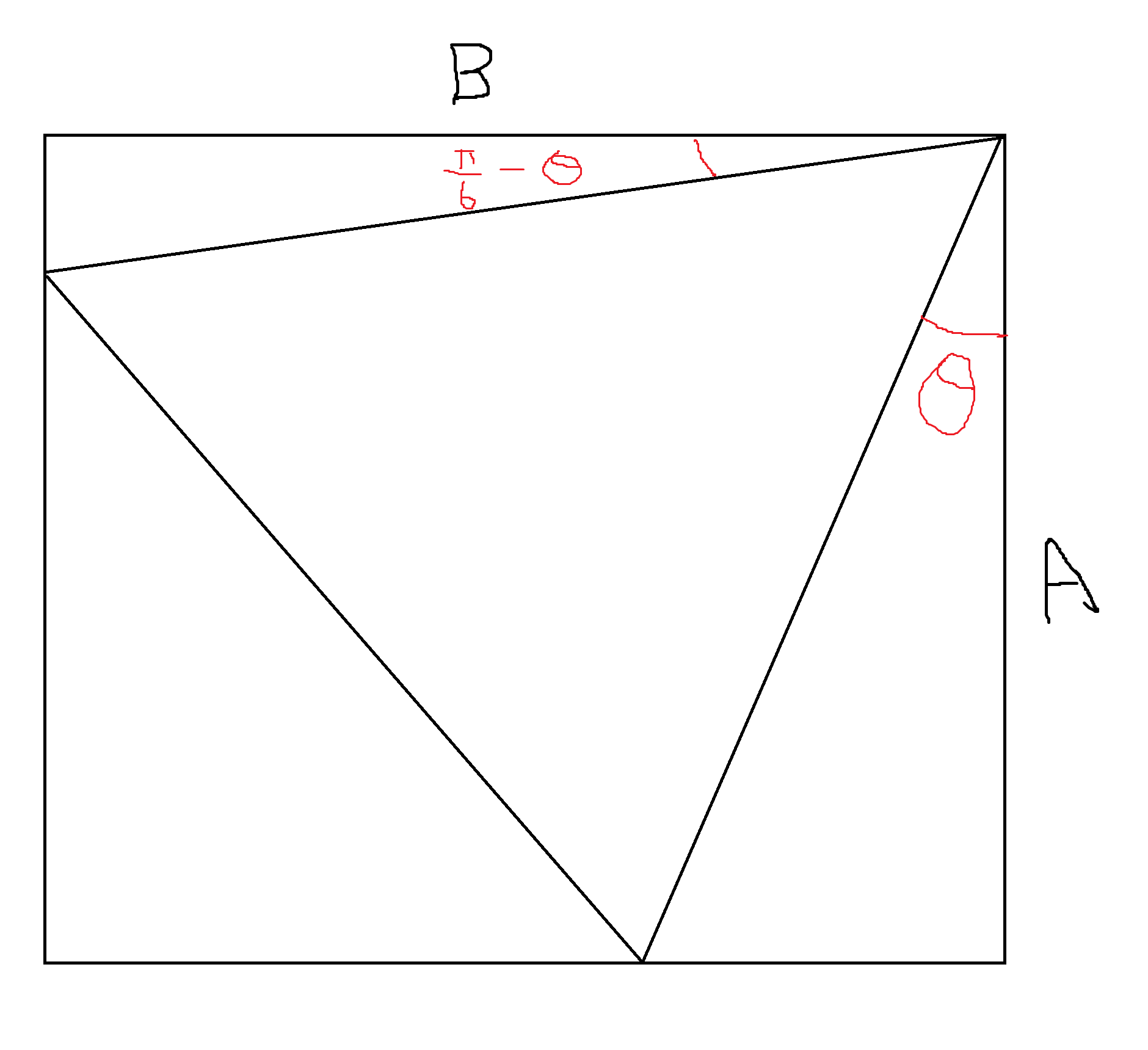
情况二就是三角形斜放,此时有\(r=\frac{A}{\cos\theta}=\frac{B}{\cos(\frac{\pi}{6}-\theta)}\)
\[A(\cos\frac{\pi}{6}\cos\theta=\sin\frac{\pi}{6}\sin\theta)=B\cos\theta\\ A(\frac{\sqrt{3}}{2}\cos\theta+\frac{1}{2}\sin\theta)=B\cos\theta\\ \frac{\sqrt 3 }{2} + \frac{\sin\theta}{2\cos\theta}=\frac B A\\ \tan\theta=\frac{2B}{A}-\sqrt 3 \]所以\(\theta=\arctan(\frac{2B}{A}-\sqrt 3),r=\frac{A}{\cos\theta}\)
#include<bits/stdc++.h>
using namespace std;
typedef long double ld;
int32_t main() {
ld a , b;
const ld SQRT3 = sqrt(3);
cin >> a >> b;
if( a > b ) swap( a , b );
if( a <= b * SQRT3 / 2.0 )
cout << fixed << setprecision(20) << a * 2.0 / SQRT3;
else {
ld theta = atan( 2*b/a - SQRT3 );
cout << fixed << setprecision(20) << a / cos(theta);
}
}