1.5、搜索算法
1.5.1、折半搜索(二分)
二分的基础的用法是在单调序列或单调函数中进行查找。因此当问题的答案具有单调性时,就可以通过二分把求解转化为判定。
1.5.1.1、标准二分
标准的二分搜索,数组中没有重复元素,如果没有这个数则返回
-1
int binarySearch1(std::vector<int> &a, int key)
{
int l = 0 ,r = a.size() - 1;
while( l <= r ){
int mid = l + (r - l) >>1;
if( a[mid] == key ) return mid;
if( a[mid] < key) l = mid + 1;
else r = mid - 1;
}
return -1;
}
我们先来分析搜索的值都是唯一的。
{1,2,5,8,9,10} 对应的下标从 0 开始,我们执行 binarySearch1(vec,8)
| 轮数 | l | r | mid | a[mid] | 变化 |
|---|---|---|---|---|---|
| 1 | 0 | 5 | 2 | 5 < key(8) | l = mid + 1 = 3 |
| 2 | 3 | 5 | 4 | 9 > key(8) | r= mid - 1 = 3 |
| 3 | 3 | 3 | 3 | 8 == key | return mid |
-
我们要找的值为
key如果a[mid] < key那么在区间a[l,mid]内都不可能存在==key的值了(单调性),所以我们将l = mid +1而不是l = mid因为a[mid]这个值肯定不在我们的解空间内。对于r = mid - 1也是相同的道理。 -
对于
while中的条件,我们可以发现我们是在最后一轮中得到的key == a[mid]所以我们需要l==r这个情况,这样写的好处就是,如果没有这个数的话直接就返回-1了,不用再写个特判。
现在我们来考虑当数组搜索的值不唯一的情况。
数组变成了 {1,2,2,4,4,4,7,7,8} ,下标也是从 0 开始,我们先执行 binarySearch1(vec,4)
| 轮数 | l | r | mid | a[mid] | 变化 |
|---|---|---|---|---|---|
| 1 | 0 | 8 | 4 | 4 | return 4 |
再执行 binarySearch(vec,7)
| 轮数 | l | r | mid | a[mid] | 变化 |
|---|---|---|---|---|---|
| 1 | 0 | 8 | 4 | 4 < key(7) | l = mid + 1 = 5 |
| 2 | 5 | 8 | 6 | 7==key | return 6 |
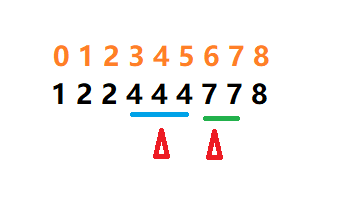
通过这两次的数据,我们可以发现,对于 binarySearch1 搜索的值出现过多次的情况下,返回的位置是不确定的。现在我们要做的事情就是让这个值确定下来,有两种优化的思路,第一个就是返回相同数中下标最小的位置,另一个为返回相同数中下标最大的位置。
1.5.1.2、返回最小下标
一个简单的思路是,只用修改 if( a[mid] == key ) 中的代码,不直接返回,而是向左遍历,直到右边不等于 key 时
if( a[mid] == key ) {
while( mid - 1 >= 0 && a[mid - 1] == key ) {mid--;}
return mid;
}
这个代码有个很明显的缺点,当数组中所有数都相同的话,算法的时间复杂度会退化到 \(\Theta (\frac{n}{2})\) ,这显然不是我们想看到的情况。
我们回到 binarySearch1(vec,4) 中
| 轮数 | l | r | mid | a[mid] | 变化 |
|---|---|---|---|---|---|
| 1 | 0 | 8 | 4 | 4 | return 4 |
在第一次的折半后 a[mid]值等于 key 值,那么 mid 值是可能成为返回的位置的,但是 [mid+1,r] 即便有 ==key 的情况,但也不是我们想要的答案了(我们想要的是下标最小的位置),所以我们改动 if(a[mid==key]) 得到 binarySearch2
int binarySearch2(int a[],int n,int key)
{
int l = 0, r = n - 1;
while( l < r ){
int mid = l + (r-l)/2;
if( a[mid] == key ) r = mid ;
else if( a[mid] < key ) l = mid + 1;
else r = mid - 1;
}
return l;
}
执行 binarySearch2(vec,4)
| 轮数 | l | r | mid | a[mid] | 变化 |
|---|---|---|---|---|---|
| 1 | 0 | 8 | 4 | 4 == key(4) | r = mid |
| 2 | 0 | 4 | 2 | 2 < key(4) | l = mid + 1= 3 |
| 3 | 3 | 4 | 3 | 4 == key(4) | r = mid = 3 |
| 4 | 3 | 3 | return 3 |
值得注意的是这里的 while 中的条件就没有等于了,也就是说当 l==r 时,就已经定位到答案了。
还有一点,如果搜索的数不存在的话,将会返回比
key小的数中最大的数,且如果这个数有多个的话,返回位置最大的那个。
1.5.1.3、返回最大下标
这就和刚才的思路是完全一样的这里就不过多赘述了直接上代码
然后在编写代码的时候就出 bug 了。如果我们直接改的话,代码是这样的
int binarySearch3(int a[],int n,int key)
{
int l = 0, r = n - 1;
while( l < r ){
int mid = l + (r-l)/2;
if( a[mid] == key ) l = mid ;
else if( a[mid] < key ) l = mid + 1;
else r = mid - 1;
}
return l;
}
执行 binarySearch3(vec,4)
| 轮数 | l | r | mid | a[mid] | 变化 |
|---|---|---|---|---|---|
| 1 | 0 | 8 | 4 | 4 == key(4) | l = mid = 4 |
| 2 | 4 | 8 | 6 | 7 < key(4) | r = mid - 1 = 5 |
| 3 | 4 | 5 | 4 | 4 == key(4) | l = mid |
| 4 | 4 | 5 | ... | 后面就死循环了 |
我们想要的是一直向右在,因为在向左走时, (l+r)/2 会自动向下取整!!,之前在分析的时候就忽略了这个,所以还要改动 mid 最终的代码:
int binarySearch3(vector<int> &a,int key)
{
int l = 0, r = a.size() - 1;
while( l < r ){
int mid = l + (r-l+1)/2;
if( a[mid] == key ) l = mid;
else if( a[mid] < key ) l = mid + 1;
else r = mid - 1;
}
return r;
}
标签:二分,返回,return,浅谈,int,mid,key,下标,模板 From: https://www.cnblogs.com/hoppz/p/17180981.html在这里如果有相同的数将会返回最右边的数,如果不存在的话返回第一个比它大的数,如果有多个的话,返回下标最小的那个