解释两类错误

1. 第一类错误：错误拒绝原假设（\(H_0\)) 的概率 ==> \(\alpha\)

2. 第二类错误：错误拒绝备择假设（\(H_1\)）的概率 ==> \(\beta\)

而第一类错误衡量的是检验的基本可信度

而第二类错误衡量的是检验效能

理解第二类错误（检验效能）的意义

如何理解 “检验效能” 中的 “效能” 二字？

首先，检验效能指代的是错误拒绝 \(H_1\) 的可能性

那么，我们首先要搞清楚什么叫 “检验”

检验

当我们对总体参数做出假设的同时，我们就需要定义一个检验，以此来衡量我们什么时候接受它，什么时候拒绝它。用如下图解释：

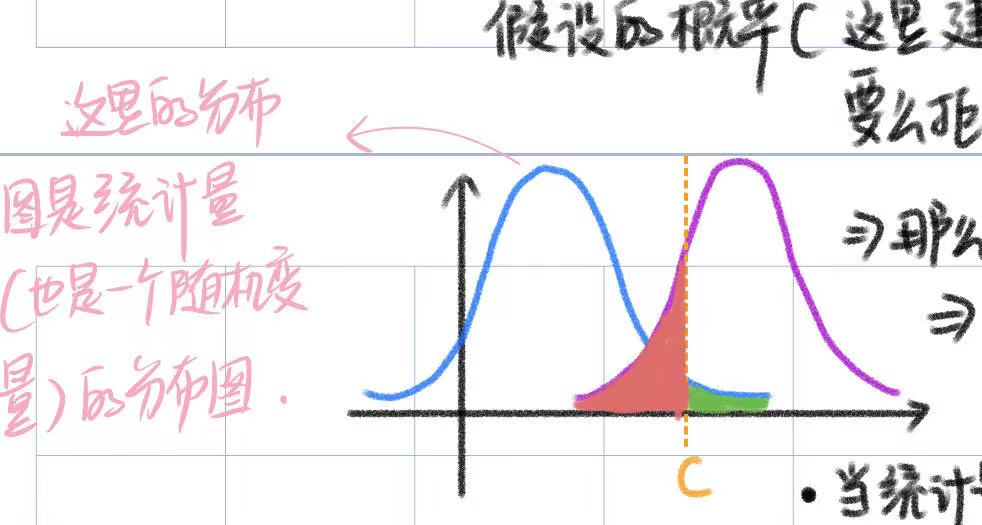
图中蓝色表示原假设条件下，统计量的分布；紫色表示备择条件下，统计量的分布。
图中的 \(c\) 就是检验的一部分：

• 当统计量 \(\bar{x} > c\) 时，拒绝原假设

• 当统计量 \(\bar{x} <= c\) 时，接受原假设

\(\bar{x}\) 与 \(c\) 的关系就构成了检验

效能

我们理解效能就离不开 \(c\) ，效能的意义就是，当我们确定了这个 \(c\) 就确定了检验。此时我们有多大的概率（红色区域的面积）犯第二类错误，即错误拒绝备择假设（ \(H_1\) )。

那么我们如何提升检验效能呢？

1. 放宽对第一类错误的要求，即增大 \(\alpha\) 。在上图中对应的情形就是 \(c\) 往左移动。当然，我们一般情况下时不愿意这么干的

2. 增大样本量。为什么增大样本量有用呢？因为 \(\bar{x}\) 分布的方差会随着样本量的增加而减小，反映在图中就是分布变窄。如下所示

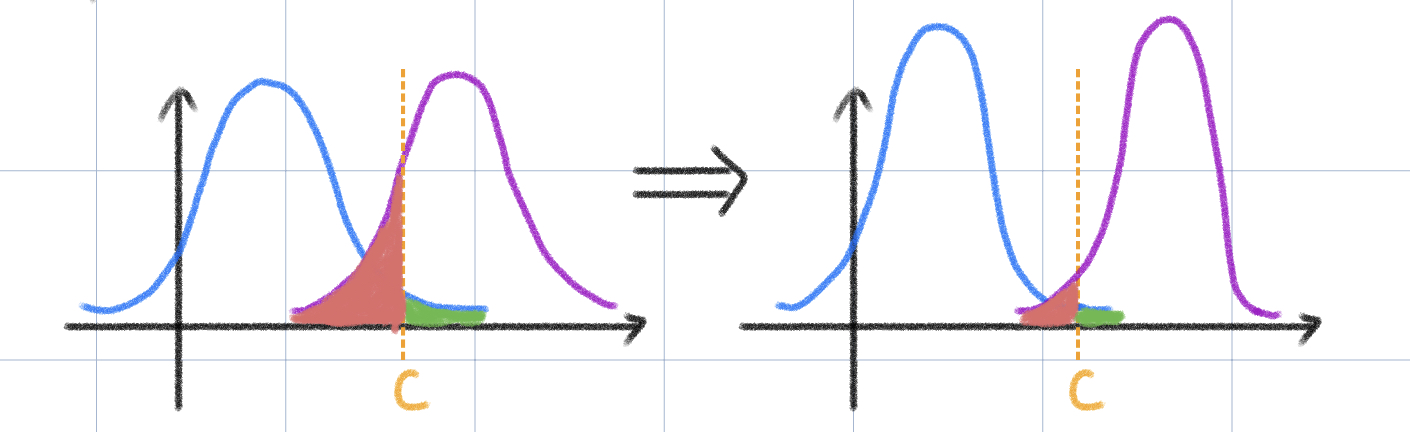
可以看到，图中红色和绿色都变小了。此时犯第一类错误和第二类错误的概率都变小了。

所以，我们一般在指定 \(\alpha\) 和 \(\beta\) 的情况下来计算所需最小的样本量来使得统计量的分布的方差达到要求。