Rook Path

题意

有一个 \(n\) 行 \(m\) 列的矩阵，有一只乌鸦在 \((x_1,y_1)\) 上，它想要去 \((x_2,y_2)\)。

乌鸦可以飞 \(k\) 次：

• 假设乌鸦现在在 \((x,y)\)，它可以选择以下两种情况中的任意一种执行。
  1. 飞到 \((x,y')\) 并且 \((y' \ne y)\)
  2. 飞到 \((x',y)\) 并且 \((x' \ne x)\)

问有多少种方法，使得 \(k\) 次操作后乌鸦能落到 \((x_2,y_2)\)。

方案数要对 \(998244353\) 取模。

对于 \(i\ (1 \leqslant i < k)\)，\(i\) 次操作后是可以在 \((x_2,y_2)\)

数据范围

• \(1 \leqslant n,m \leqslant 10 ^ 9\)
• \(1 \leqslant k \leqslant 10 ^ 6\)
• \(1 \leqslant x_1,x_2 \leqslant n\)
• \(1 \leqslant y_1,xy_2 \leqslant m\)

思路

爆搜是不可能AC的。

但是，通过暴力输出dp数组，我们可以发现：不是每种情况都是需要算的，某些情况是重复的！

结果可以分为四类，如下图，每种颜色代表一种答案。

• 设起点为 \((x_1,y_1)\)
  1. \((x_1,y_1)\)
  2. \((x_1,y) (y \ne y_1)\)
  3. \((x,y_1) (x \ne x_1)\)
  4. \((x,y) (x \ne x_1,y \ne y_1)\)

继续画图来找规律

下面的同行同列指的是与起点同行或同列。

1|\((x_1,y_1)\)

同行同列的格子可以转移到这个格子上

• 同行格子数（减去起点）：\(m - 1\)
• 同列格子数（减去起点）：\(n - 1\)

2|\((x_1,y) (y \ne y_1)\)

同行的格子、起点以及不同行且不同列的格子可以转移到这个格子上

• 同行格子数（减去起点和自己）：\(m - 2\)
• 起点：\(1\)
• 不同行且不同列的格子：\(n - 1\)

3|\((x,y_1) (x \ne x_1)\)

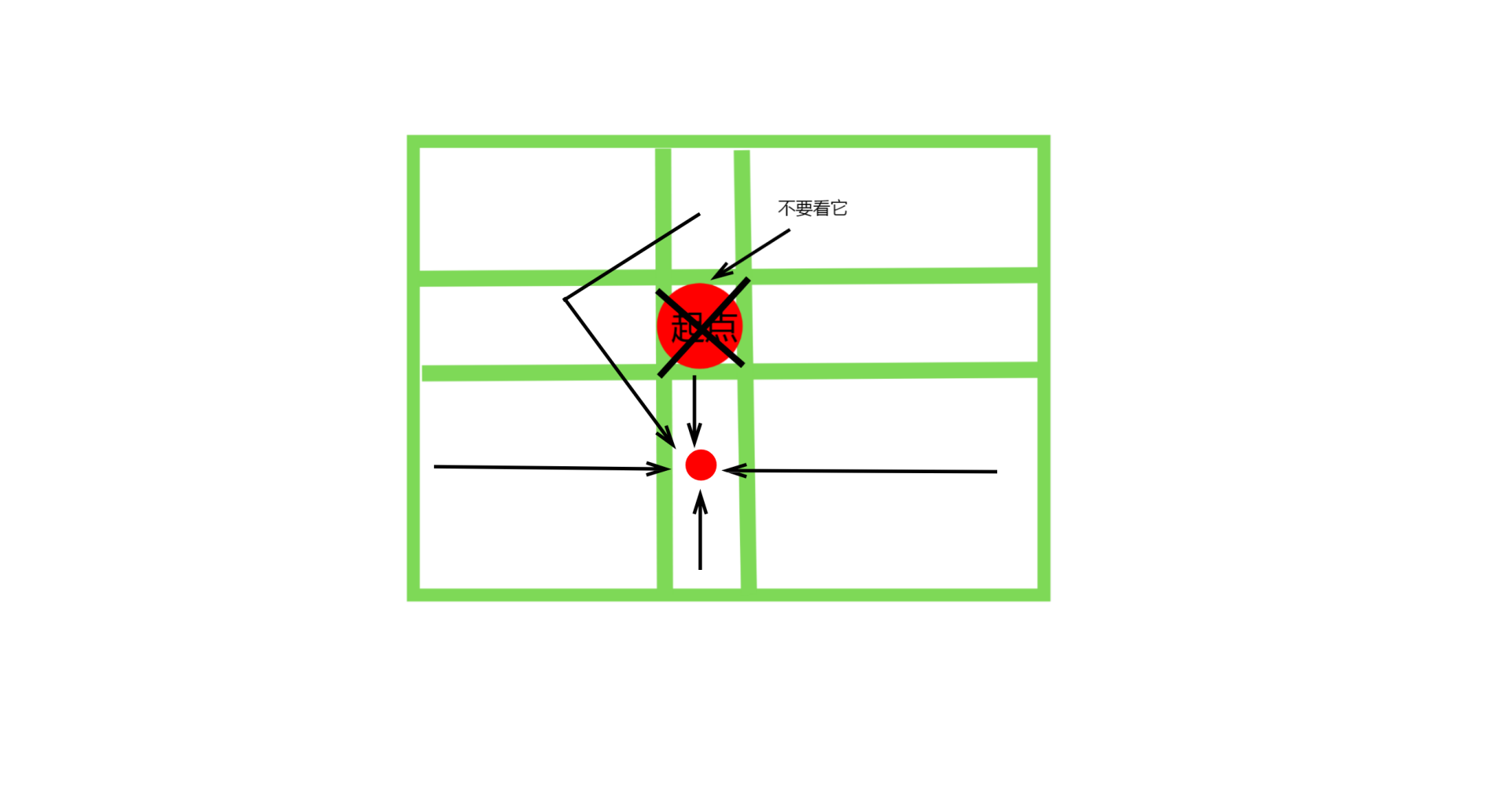
同列的格子、起点以及不同行且不同列的格子可以转移到这个格子上

• 同列格子数（减去起点和自己）：\(n - 2\)
• 起点：\(1\)
• 不同行且不同列的格子：\(m - 1\)

4|\((x,y) (x \ne x_1,y \ne y_1)\)

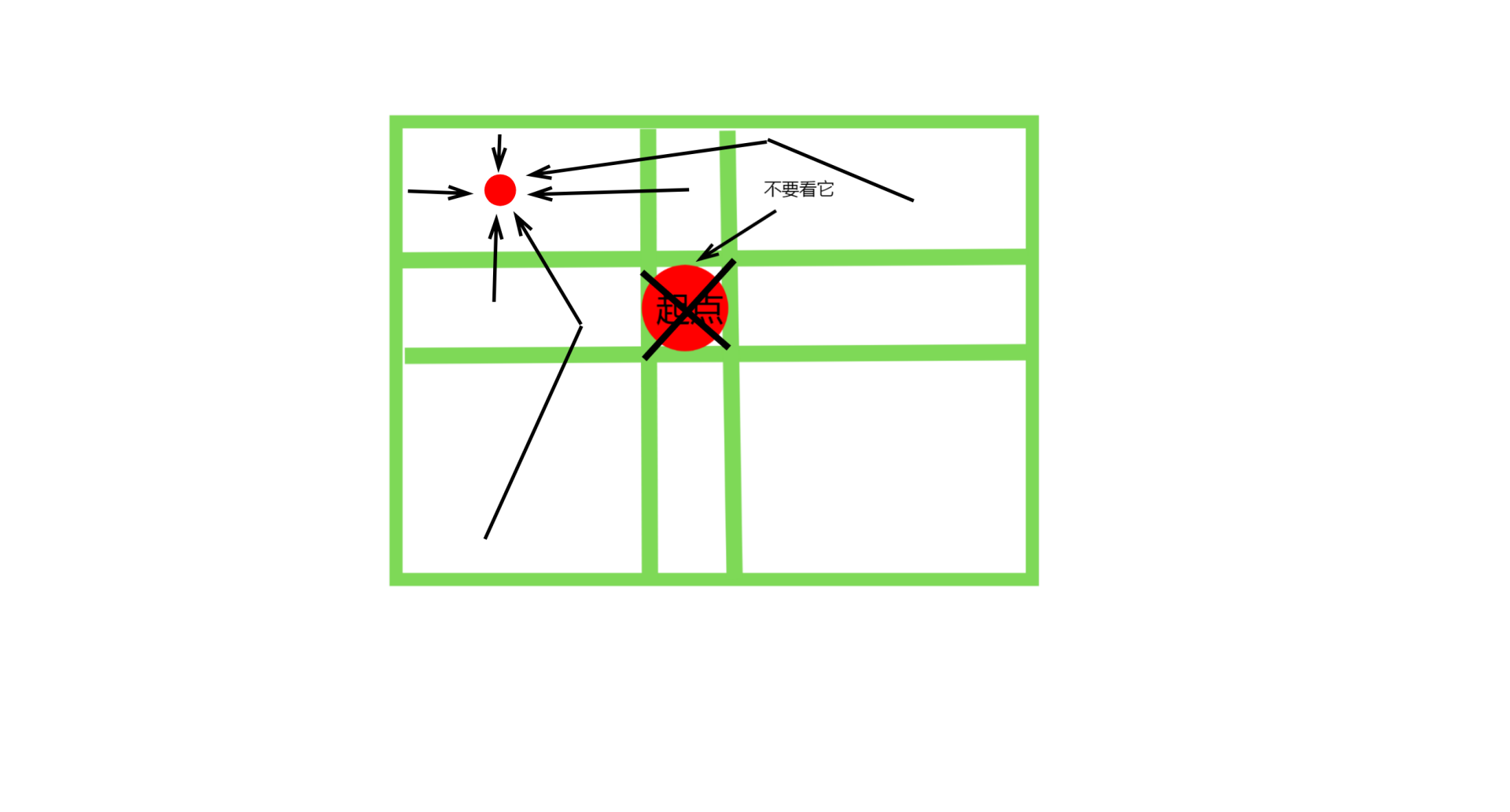
同列的格子、同行的格子以及不同行且不同列的格子可以转移到这个格子上

• 同列格子数：\(1\)
• 同行格子数：\(1\)
• 不同行且不同列的格子：\(n + m - 4\)

复杂度

• 时间：\(O(k)\)
• 空间：\(O(4 \times k)\)

Code

#include <iostream>
#include <vector>
#include <queue>

using namespace std;

const int mod = 998244353, K = 1e6 + 1;

int n, m, k, sx, sy, ex, ey;
long long dp[K][6], ans;

int main(){
  ios::sync_with_stdio(0), cin.tie(0);
  cin >> n >> m >> k >> sx >> sy >> ex >> ey;
  dp[0][0] = 1;
  for (int i = 1; i <= k; i++) {
    dp[i][0] = (dp[i - 1][1] * (m - 1) % mod + dp[i - 1][2] * (n - 1) % mod) % mod;
    dp[i][1] = (dp[i - 1][0] + dp[i - 1][1] * (m - 2) % mod + dp[i - 1][3] * (n - 1) % mod) % mod;
    dp[i][2] = (dp[i - 1][0] + dp[i - 1][3] * (m - 1) % mod + dp[i - 1][2] * (n - 2) % mod) % mod;
    dp[i][3] = (dp[i - 1][1] + dp[i - 1][2] + dp[i - 1][3] * (n + m - 4) % mod) % mod;
  }
  if (ex == sx && ey == sy) {
    ans = dp[k][0];
  } else if (ex == sx) {
    ans = dp[k][1];
  } else if (ey == sy) {
    ans = dp[k][2];
  } else {
    ans = dp[k][3];
  }
  cout << ans;
  return 0;
}