BIT学习笔记

基础树状数组：

先放一张图：

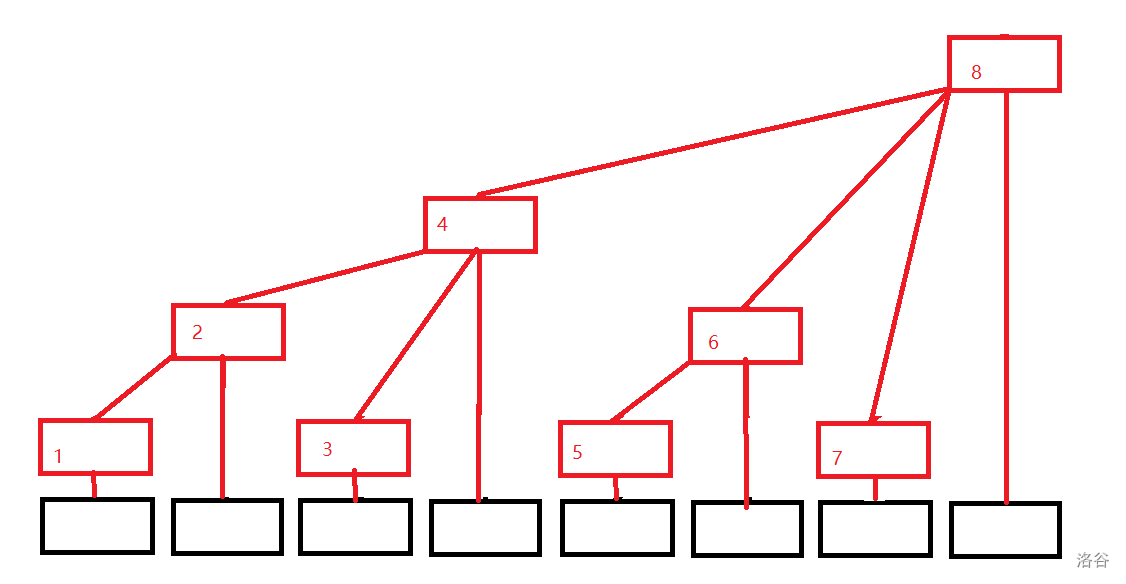
图中黑色的框为 \(a\) 数组（原数组）。

图中黑色的框为 \(t\) 数组（树状数组）。

我们可以得到 $t[i]= \sum_{j=1}^{j \le 2^k}{a[i-2k+j]} $。

在这里，\(k\) 为 \(i\) 的二进制中从最低位到高位连续零的长度。

那我们要如何求这个 \(k\) 呢？

我们需要用到一个东西叫 lowbit 它就是求二进制从后往前数的第一个 \(1\)。

它是这样实现的：

#define lowbit(x) (x&-x)

这么简单?对，就这么简单。

证明可以看这篇博客。

知道了这些，我们就可以打出支持单改区查的树状数组了。

单点修改：

inline void add(int x,int k){
	for(int i=x;i<=n;i+=lowbit(i))
		tr[i]+=k;
}

区间查询：

inline int _qry(int x){
	int res(0);
	for(int i=x;i;i-=lowbit(i))
		res+=tr[i];
	return res;
}
#define qry(l,r) (_qry(r)-_qry(l-1))

用上差分还可以实现区改单查：

区间修改：

inline void _add(int x,int k){
	for(int i=x;i<=n;i+=lowbit(i))
		tr[i]+=k;
}
#define add(l,r,x) _add(l,x),_add(r+1,-x)

单点查询：

inline int qry(int x){
	int res(0);
	for(int i=x;i;i-=lowbit(i))
		res+=tr[i];
	return res;
}

树状数组拓展：

单点修改，区间查询最值:

int tr[MAXN],a[MAXN],n;
inline void add(int x,int k){
	a[x]+=k;
	for(int i=x;i<=n;i+=lowbit(i))
		tr[i]=max(tr[i],a[x]);
}
inline int qry(int l,int r){
	return (r<=l?a[l]:(r-lowbit(r)>l?max(tr[r],qry(l,r-lowbit(r))):max(a[r],qry(l,r-1))));
}

离线后区间查不同的数个数（HH的项链）:

#include<bits/stdc++.h>
#define MAXN 1000005
using namespace std;
struct que{
	int l,r,ID;
	inline bool operator<(const que &x)const{
		return r<x.r;
	}
}q[MAXN];
int n,a[MAXN],ans[MAXN],num[MAXN],tr[MAXN];
#define lowbit(x) (x&-x)
inline void add(int x,int k){
	for(int i=x;i<=n;i+=lowbit(i))
		tr[i]+=k;
}
inline int qry(int x){
	int ans(0);
	for(int i=x;i;i-=lowbit(i))
		ans+=tr[i];
	return ans;
}
int main(){
	int m,k(1);
	scanf("%d",&n);
	for(int i=1;i<=n;i++)
		scanf("%d",&a[i]);
	scanf("%d",&m);	
	for(int i=1;i<=m;i++)
		scanf("%d%d",&q[i].l,&q[i].r),q[i].ID=i;
	sort(q+1,q+m+1);
	for(int i=1;i<=n;i++){
		if(num[a[i]])add(num[a[i]],-1);
		add(i,1),num[a[i]]=i;
		int as=qry(i);
		while(q[k].r==i)ans[q[k].ID]=as-qry(q[k].l-1),k++;
	}
	for(int i=1;i<=m;i++)
		printf("%d\n",ans[i]);
    return 0;
}

求逆序对:

#include<bits/stdc++.h>
#define MAXN 500005
#define lowbit(x) (x&-x)
using namespace std;
int tr[MAXN],n;
inline void add(int x,int k){
	for(int i=x;i<=n;i+=lowbit(i))
		tr[i]+=k;
}
inline int qry(int x){
	int res(0);
	for(int i=x;i;i-=lowbit(i))
		res+=tr[i];
	return res;
}
int a[MAXN],b[MAXN];
unordered_map<int,int>m;
signed main(){
	long long ans(0);
	scanf("%d",&n);
	for(int i=1;i<=n;i++)
		scanf("%d",&a[i]),b[i]=a[i];
	sort(b+1,b+n+1);//这里是离散化
	for(int i=1;i<=n;i++)
		m[b[i]]=i;//离散化
	for(int i=1;i<=n;i++)
		a[i]=m[a[i]],//离散化
		add(a[i],1),
		ans+=i-qry(a[i]);
	printf("%lld",ans);
	return 0;
}