D. Range Add Query
题意:有一个序列 \(A\) 和正整数 \(k\),每次询问给定 \(l,r\),你可以在 \([l,r]\) 内选择一段长度为 \(k\) 的子段,统一加减,问是否能将 \([l,r]\) 全部变为 \(0\)。\(n,q\le 2\times 10^5,k\le 10\)
考虑操作在差分数组上的体现:选两个距离为 \(k\) 的位置,一边加一边减。于是,在 \([l,r]\) 内,各个模 \(k\) 同余类是独立的。对于每个同余类,元素和不会改变,在此基础上任意改变,所以要求元素和为 \(0\) 即可。
By jiangly
#include <bits/stdc++.h>
using i64 = long long;
int main() {
std::ios::sync_with_stdio(false);
std::cin.tie(nullptr);
int n, k;
std::cin >> n >> k;
std::vector<int> a(n);
std::vector<i64> s(n);
for (int i = 0; i < n; i++) {
std::cin >> a[i];
s[i] = a[i];
if (i >= k) {
s[i] += s[i - k];
}
}
int q;
std::cin >> q;
while (q--) {
int l, r;
std::cin >> l >> r;
l--, r--;
std::vector<i64> b(k);
for (int i = r; r - i + 1 <= k; i--) {
b[i % k] += s[i];
}
for (int i = l - 1; i >= 0 && l - i <= k; i--) {
b[i % k] -= s[i];
}
if (b == std::vector(k, b[0])) {
std::cout << "Yes\n";
} else {
std::cout << "No\n";
}
}
return 0;
}
E. Wish List
题意:一个商店有 \(n\) 个商品,你需要买其中的 \(m\) 个(告诉你是哪 \(m\) 个)。每个商品有本身的价格 \(a_i\),如果你买的商品在剩余商品中排第 \(i\) 位,则需额外付 \(c_i\) 元。如果需要,你也可以买 \(m\) 个之外的物品。问最小价格。\(n,m\le 5000\)
容易发现,后面如何选对前面没有影响,但前面如何选对后面有影响。如果不知道前面的状态,后面的完全无法确定。所以考虑从前往后 DP。
设 \(f[i][j]\) 表示前 \(i\) 个商品,钦定买 \(j\) 个(一定要把该买的买完)的最小价格。转移时,考虑第 \(i\) 个商品买不买。如果买,则为 \(f[i-1][j-1]+a_i+c[x]\)。考虑 \(x\) 能选的范围,显然由于钦定前面只选 \(j-1\) 个,所以 \(x\ge i-j+1\)。但是只能排这个吗?当然不是。可以在选前面 \(j-1\) 个的过程中把第 \(i\) 个商品买掉。在这个过程中,\(i\) 排多少名都可以,所以 \(i-j+1\le x\le i\)。这个可以用 ST 表/暴力预处理维护一下。
如果不买,则为 \(f[i-1][j]\)。但是对于需要买的商品必须买,没有这一项。
By apaid
const int N=5010;
int n,m,a[N],c[N],mark[N],mn[N][N];
ll dp[N][N];
int main() {
scanf("%d%d",&n,&m);
rep(i,0,n) scanf("%d",&a[i]);
rep(i,0,n) scanf("%d",&c[i]);
rep(i,0,n) {
mn[i][i]=c[i];
rep(j,i+1,n) mn[i][j]=min(mn[i][j-1],c[j]);
}
rep(i,0,m) {
int x;
scanf("%d",&x);
--x;
mark[x]=1;
}
memset(dp,0x20,sizeof(dp));
dp[0][0]=0;
rep(i,0,n) rep(j,0,i+1) {
dp[i+1][j]=min(dp[i+1][j],dp[i][j]+a[i]+mn[j][i]);
if (!mark[i]) dp[i+1][j+1]=min(dp[i+1][j+1],dp[i][j]);
}
ll ans=1ll<<60;
rep(j,0,n+1) ans=min(ans,dp[n][j]);
printf("%lld\n",ans);
}
F. Integer Division
题意:有一个长度为 \(n\) 的数字串,将其划分成若干段,一种划分方案的权值为每段表示的数的乘积。求所有划分方案的权值和,对 \(998244353\) 取模。\(n\le 2\times 10^5\)
设 \(f[i]\) 表示前 \(i\) 个数,最后一段以 \(i\) 结尾划分方案的权值之和,则 \(f[i]=\sum\limits_{j<i}f[j]\times c(j+1,i)\)。进一步转化,设 \(s[i]\) 表示前 \(i\) 位的数字加上 \(n-i\) 个 \(0\) 得到的数,则
\[\begin{aligned} f[i]&=\sum f[j]\times\frac{s[i]-s[j]}{10^{n-i}}\\ &=\frac{1}{10^{n-i}}\left(s[i]\sum f[j]-\sum f[j]s[j]\right) \end{aligned} \]分别维护 \(f[j]\) 的前缀和与 \(f[j]s[j]\) 的前缀和即可。
By cxm1024
#include <bits/stdc++.h>
using namespace std;
#define int long long
const int mod = 998244353;
int ksm(int a, int b, int res = 1) {
for(; b; a = a * a % mod, b >>= 1)
if(b & 1) res = res * a % mod;
return res;
}
int inv(int x) {return ksm(x, mod - 2);}
int f[200010], s[200010], t[200010], sumf[200010], sumfs[200010];
signed main() {
int n;
string x;
cin >> n >> x;
int now = 1;
for(int i = n - 1; i >= 0; i--, now = now * 10 % mod)
t[i + 1] = (x[i] - '0') * now % mod;
for(int i = 1; i <= n; i++)
s[i] = (s[i - 1] + t[i]) % mod;
f[0] = 1, sumf[0] = 1, sumfs[0] = 0;
for(int i = 1; i <= n; i++) {
f[i] = (sumf[i - 1] * s[i] % mod - sumfs[i - 1] + mod) % mod;
(f[i] *= inv(ksm(10, n - i))) %= mod;
sumf[i] = (sumf[i - 1] + f[i]) % mod;
sumfs[i] = (sumfs[i - 1] + f[i] * s[i] % mod) % mod;
}
cout << f[n] << endl;
return 0;
}
G. 3^N Minesweeper
题意:有一个 \(0\sim 3^n-1\) 的 \(01\) 数组 \(a\),生成一个数组 \(b\),其中 \(b_i\) 表示与 \(i\) 相邻的 \(j\) 的 \(a_j\) 之和。两个数相邻的定义为,三进制下每个对应位的距离都不超过 \(1\)。已知 \(b\),求 \(a\)。
对于 \(n=2\) 的情况,题意转化为类似扫雷的局面,区别在于这里的雷数包括自己。本题的题意相当于 \(n\) 维空间的边长为 \(3\) 的扫雷。这里以二维为例:
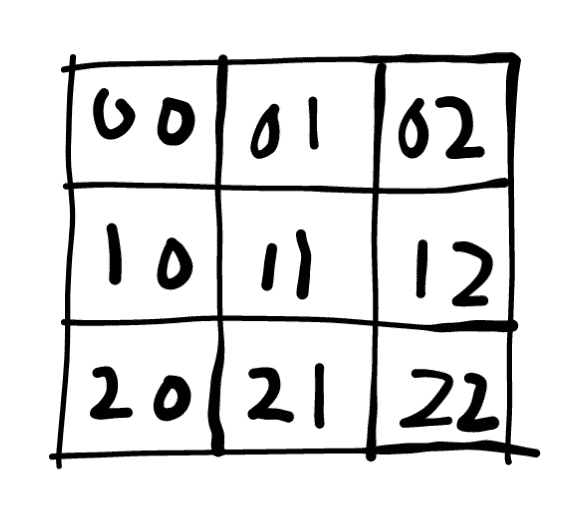
要想知道每个格子是否有雷,可以进行“降维打击”。具体地:
\[\begin{cases} a[10]+a[12]-a[11]=b[01]+b[11]+b[21]\\ a[00]+a[02]-a[01]=b[01]+b[11]\\ a[20]+a[22]-a[21]=b[21]+b[11] \end{cases} \]容易发现,右边的三个量恰好等于中间那列在一维问题上的 \(a'\),可以递归解出。进一步:
\[\begin{cases} a[10]-a'[11]=a'[10]\\ a[00]-a'[01]=a'[00]\\ a[20]-a'[21]=a'[20] \end{cases} \]即可得出左边列作为一维问题的 \(a'\),右边同理递归处理即可。
在实现上,选择两个“边”和一个“中间”来进行容斥,它们只有一位的差距,中间块该位为 \(1\),两边的块分别为 \(0,2\)。代码既可以采用递归的模拟写法,也可以直接循环,每次降一维。
递归 By cxm1024
#include <bits/stdc++.h>
using namespace std;
int n, e[13], f[600000];
void solve(int now, int nowx) {
if(now == n + 1) return;
int tmp = e[now];
now++;
for(int i = 0; i < e[n - now]; i++)
f[nowx + tmp + i * e[now]] = f[nowx + i * e[now]] + f[nowx + tmp * 2 + i * e[now]] - f[nowx + tmp + i * e[now]];
for(int i = 0; i < e[n - now]; i++) {
f[nowx + i * e[now]] -= f[nowx + tmp + i * e[now]];
f[nowx + 2 * tmp + i * e[now]] -= f[nowx + tmp + i * e[now]];
}
solve(now, nowx + tmp);
solve(now, nowx), solve(now, nowx + 2 * tmp);
}
signed main() {
e[0] = 1;
for(int i = 1; i <= 12; i++)
e[i] = e[i - 1] * 3;
cin >> n;
for(int i = 0; i < e[n]; i++)
cin >> f[i];
solve(0, 0);
for(int i = 0; i < e[n]; i++)
cout << f[i] << " ";
cout << endl;
return 0;
}
循环 By miao22
#include<bits/stdc++.h>
using namespace std;
int n,a[1000003],m;
int main(){
ios::sync_with_stdio(0);
cin.tie(NULL);
cout.tie(NULL);
cin>>n;
m=pow(3,n);
for(int i=0;i<m;i++)
cin>>a[i];
int pw=1;
for(int i=0;i<n;i++){
for(int j=0;j<m;j++)
if(j%(pw*3)<pw){
int x=a[j],y=a[j+pw],z=a[j+pw+pw];
a[j]=y-z;
a[j+pw]=x+z-y;
a[j+pw+pw]=y-x;
}
pw*=3;
}for(int i=0;i<m;i++)
cout<<a[i]<<' ';
}