前言
前排提示:由于作者水平很菜,所以本篇文章不会讲最优性证明、复杂度证明。如有需要请自行搜索
前排提示2;本文巨无敌长,阅读并完全理解可能需要 \(1\sim 2\) 小时。但对于 SAM 这种恐怖算法来说,\(2\) 小时其实并不多(毕竟我当初断断续续学了两天才理解)。
前排提示3:可能有点啰嗦,但在能忍受的情况下建议看完,会加深理解。
本篇文章的例子和插图全部来自 pecco 大佬的博客,作者也是通过那篇文章学会的 SAM。但那篇文章的思维跳跃比较快,有些理解写的也不是很完整(大佬博客通病),这篇文章可以看作那篇文章的详细版、简单版。
SAM 是干什么的
SAM,后缀自动机,顾名思义,是后缀的自动机(划掉)。可以理解为一个升级版的 trie 树,其中 trie 树内保存某字符串的所有后缀。例如,对于字符串 \(s=\texttt{aababc}\),其 trie 树如下:
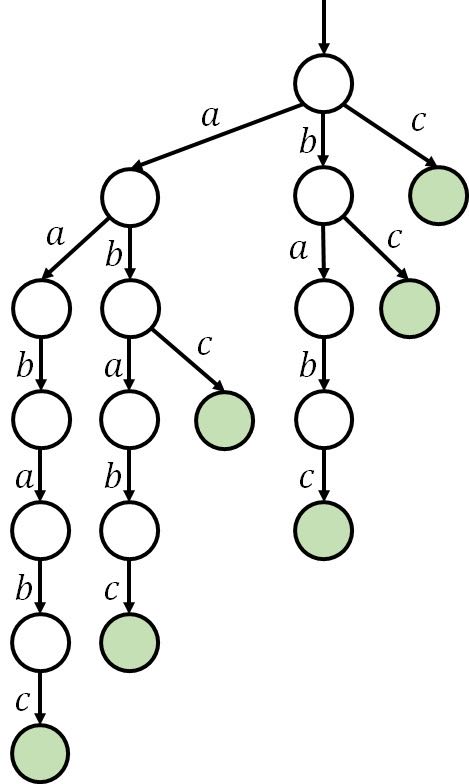
用 trie 树存字符串的每个后缀的其中一个用处为,可以快速地找到一个字符串 \(t\) 是否在 \(s\) 中出现(当然不止这一个用途,最后会讲应用)。
容易发现,这种 trie 树包含了很多浪费,如下图:
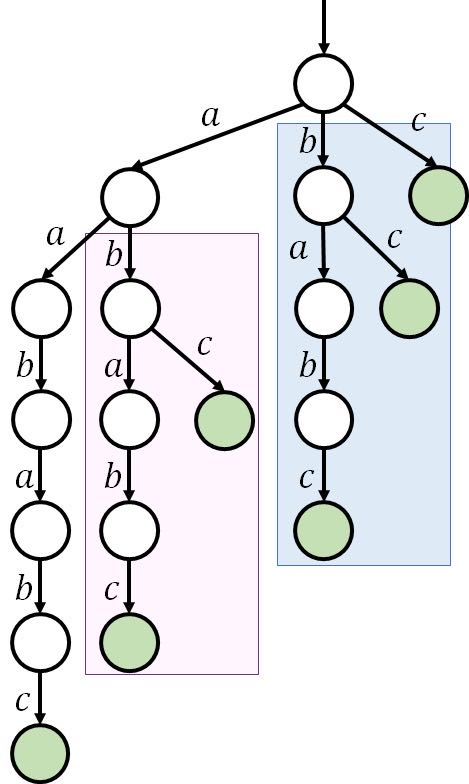
紫色的部分和蓝色的部分结构完全一样,所以可以从根节点直接连一个 \(\texttt{b}\) 的边,指向 \(\texttt{ab}\) 的节点。SAM 就可以理解成没有任何浪费的 trie 树。想法很自然,但如何形式化的完善这一想法呢?
endpos 集合与 parent tree
定义一个函数 \(\mathrm{endpos}(t)\),表示一个字符串 \(t\) 在 \(s\) 中所有出现的结束位置集合。如,对于上面的例子 \(s=\texttt{aababc}\),\(\mathrm{endpos}(\texttt{ab})=\{3,5\}\)。
另一种直观的理解方式为,我当前从字符串 \(s\) 上某个位置开始走,知道我依次经过了 \(t\) 的字符串,那么 \(\mathrm{endpos}(t)\) 会告诉我,当前我可能处在哪些位置。
我们发现,对于上面例子 \(s=\texttt{aababc}\) 来说,\(\mathrm{endpos}(\texttt{b})=\mathrm{endpos}(\texttt{ab})=\{3,5\}\),那么在上面的 trie 树上,\(\texttt{b}\) 和 \(\texttt{ab}\) 的节点子树完全相同。感性理解,我走了 \(\texttt{b}\) 和 \(\texttt{ab}\) 后可能所处的位置完全相同,那么后面能怎么走自然也完全相同。
于是我们可以得出一个结论:在 SAM 中,\(\mathrm{endpos}\) 相同的字符串可以共用一个节点。形式化地,将 \(s\) 的所有子串 \(t\) 划分成若干个“\(\mathrm{endpos}\) 等价类”,则每个等价类与 SAM 上的节点一一对应。
我们显然不能暴力地去找每一个等价类,这就引出了一个新概念:parent tree。它建立了所有 \(\mathrm{endpos}\) 等价类之间的关系。
还是以 \(s=\texttt{aababc}\) 来说。如果我当前走了 \(\texttt{a}\),那么我当前可能在 \(\{1,2,4\}\)。但如果我当前走了 \(\texttt{ba}\),我当前只可能在 \(\{4\}\)。此时,在一个字符串前加上一个新的字符,可能会产生新的限制,从而将集合分裂出去。parent tree 上的边表示的就是这种分裂。
对于 \(s=\texttt{aababc}\),parent tree 的形态如下:
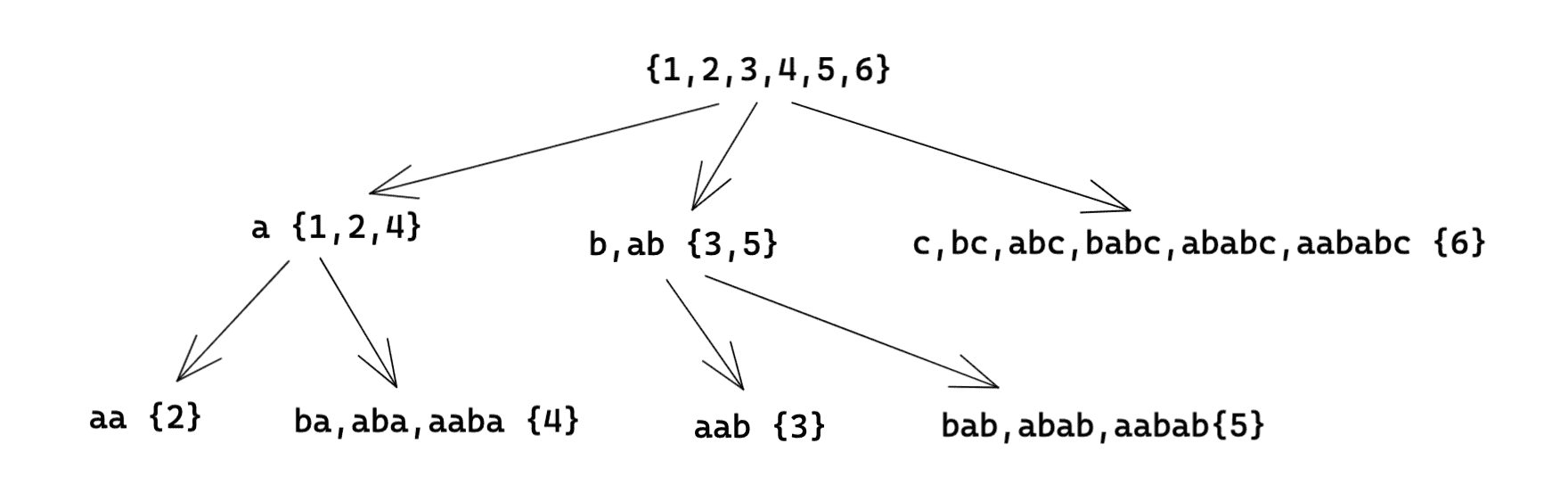
这里说一下对于这张图的感性理解:假如我走了一步,经过 \(\texttt{b}\),我当前可以在 \(\{3,5\}\)。如果我加强了限制,走了两步,为 \(\texttt{ab}\),那么我当前仍可能在 \(\{3,5\}\)。如果我走了三步,为 \(\texttt{bab}\),那么我只能在 \(\{5\}\)。同理,如果走了四步,为 \(\texttt{abab}\),同样只能在 \(\{5\}\)。
通过感性理解可以发现,parent tree 有几个非常重要的性质:
- 一个点代表的若干个字符串为最长的字符串的后缀,且长度连续(不可能出现代表 \(\texttt{d,bcd,abcd}\) 而不代表 \(\texttt{cd}\)。
- 一个节点的祖先为该节点字符串的后缀,且依次往上遍历可以遍历到所有后缀。
- 由性质 2 推出,一个节点的最短字符串长度为,父亲节点的最长长度\(+1\)。
接下来考虑 parent tree 的节点数(即不同的等价类个数,也就是 SAM 的节点数)。由于叶子节点的集合元素个数为 \(1\),每个节点的元素个数都至少为儿子之和,最终根节点元素个数为 \(n\),所以总节点数不会超过 \(2n-1\)(易证,这里不赘述)。
构建 SAM
来到重头戏了!在这里,我们采取动态构造的方法,依次加入每个字符,并同时维护 parent tree 和 SAM。因为两者的节点一一对应,所以我们在同一个结构体里维护:
struct node {
int fa,nxt[26],len;
} sam[MAXN*2];
其中 sam[u].fa 表示 \(u\) 在 parent tree 上的父亲,sam[u].nxt[ch] 表示 \(u\) 在 SAM 上经过 \(ch\) 到达的节点,sam[u].len 表示 \(u\) 所表示的最长字符串的长度。最短长度即为 sam[sam[u].fa].len+1。
这里先把算法流程过一遍,有一个框架,后面再详细说明。
首先有根节点,这里设为 \(1\) 号节点。
加入字符的过程中,维护当前整个串对应的节点 \(lst\)。
加入一个字符 \(ch\) 时,新建一个节点 \(cur\) 表示整个串(也可能表示了其他串,但整串是最长的)。
从 \(lst\) 开始在 parent tree 上往上爬,直到爬到一个节点 \(p\) 已经存在 \(ch\) 的出边。在这之前,每个节点都没有 \(ch\) 的出边,所以新建一个 \(ch\) 的出边指向 \(cur\)。
如果爬完了 parent tree,每个节点都没有 \(ch\) 的出边,则将
sam[cur].fa设为根。否则,设碰到的节点为 \(p\xrightarrow{ch}q\),作如下判断:
- 如果
sam[p].len+1==sam[q].len,那么将sam[cur].fa设为 \(q\),结束。- 否则,新建一个节点 \(r\),信息与 \(q\) 完全相同,但
sam[r].len=sam[sam[q].fa].len+1,并将sam[q].fa和sam[cur].fa改为 \(r\)。接下来,让 \(p\) 继续往上爬,对于每个 \(p\xrightarrow{ch}q\) 改为 \(p\xrightarrow{ch}r\)。最后将当前整个串的节点
lst改为cur。
int cnt=1,lst=1;
void insert(int ch) {
int cur=++cnt,p=lst;
sam[cur].len=sam[lst].len+1;
for(;p&&!sam[p].nxt[ch];p=sam[p].fa)
sam[p].nxt[ch]=cur;
int q=sam[p].nxt[ch];
if(!q) sam[cur].fa=1;
else if(sam[p].len+1==sam[q].len) sam[cur].fa=q;
else {
int r=++cnt;
sam[r]=sam[q],sam[r].len=sam[p].len+1;
for(;p&&sam[p].nxt[ch]==q;p=sam[p].fa)
sam[p].nxt[ch]=r;
sam[q].fa=sam[cur].fa=r;
}
lst=cur;
}
看完肯定非常晕,但没关系,我们接下来通过一个例子,将每一步的原理解释清楚。
对于 \(s=\texttt{aababb}\),我们模拟一遍上述过程。前面的两个字符不具有代表性,我们从第三个开始。
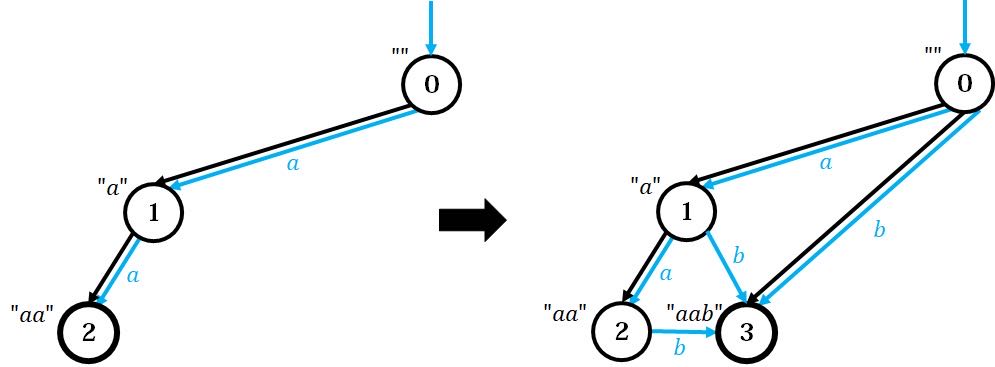
左图为加入前两个字符 \(\texttt{aa}\) 后的形态,右图新加入了字符 \(\texttt{b}\)。观察左图,根据前面说的过程,找到原先整个串对应的节点 \(2\),顺着黑色的 tree 边往上爬。容易发现,一直到根节点,每个节点都不存在 \(\texttt{b}\) 的出边。于是将每个点走 \(b\) 的出边连向新点 \(3\)。
我们当然不只是模拟过程,接下来进行解释:
根据 tree 的性质,在原图上往上爬一定能遍历原串所有的后缀,且是从长往短遍历。我们希望让新图也能存下新串的所有后缀,而新串的后缀等于原串后缀+字符 \(\texttt{b}\)。所以,如果一个原串后缀没有字符 \(\texttt{b}\) 的出边,就说明对应的这个新串后缀没有被保存过,必须向新点连 \(\texttt{b}\) 的边。连边的意思是,让原串后缀点+字符 \(\texttt{b}\) 得到的新串后缀,归属这个新点。
这里一直到根节点都不存在 \(\texttt{b}\) 的出边,也就说明原串中不存在任何一个新串的后缀。然而,新节点的 fa 必须为新串的后缀,所以只能连表示空串的根节点了。
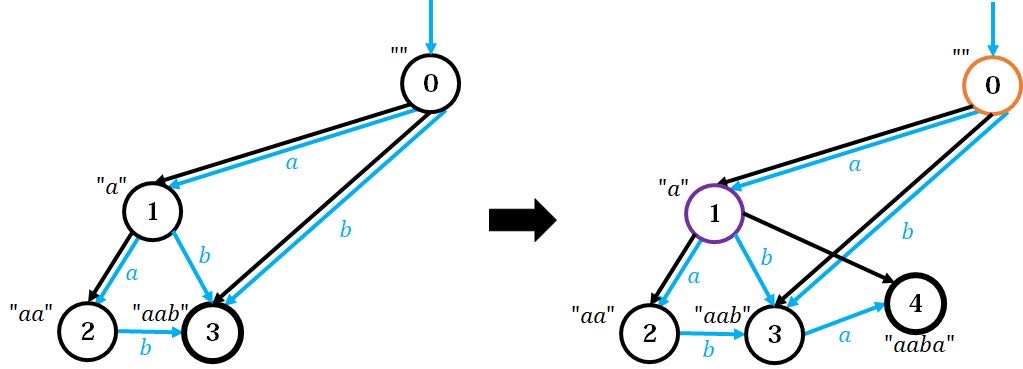
左图为加入 \(\texttt{aab}\) 后的形态,右图为新加入字符 \(\texttt{a}\) 后的形态。观察左图,同样模拟一开始说的过程:找到整个串对应的节点 \(3\),没有 \(\texttt{a}\) 的出边,所以连到新节点 \(4\);往上爬到 \(0\),发现 \(0\) 已经有了一条 \(a\) 的出边指向 \(1\),且 \(1\) 的 \(len\) 等于 \(0\) 的 \(len+1\),所以将新点 \(4\) 的 fa 设为 \(1\)。
事情就是从这里开始奇怪的。这里的过程明显比上面难懂,解释如下:
考虑节点 \(3\) 表示的字符串有哪些。容易发现,在原串的所有后缀中,\(\texttt{aab,ab,b}\) 归到节点 \(3\)。由于能归到同一个节点,它们同属一个等价类,也就是对后面的影响可以看作等价的。这个节点不存在 \(\texttt{a}\) 的出边,意味着原串不存在 \(\texttt{aaba,aba,ba}\),但这些都是新串的后缀。那么我们将这个节点连到 \(4\),就意味着让 \(\texttt{aaba,aba,ba}\) 都归属到节点 \(4\)。但是新串的后缀不止有这三个,还有更短的 \(\texttt{a}\) 等,于是继续往上跳。
跳到了节点 \(0\),它表示的字符串为空串,通过字符 \(\texttt{a}\) 的出边自然就是 \(\texttt{a}\)。这里已经有节点 \(1\) 表示 \(\texttt{a}\) 了,说明新串的后缀 \(\texttt{a}\) 已经在原串中出现过,那么就不需要让 \(\texttt{a}\) 来归属 \(4\) 了,只需归属 \(1\) 即可。为了让 \(4\) 往上跳能跳到所有后缀,我们让它的 fa 设为 \(1\)。如果有更短的后缀,自然也在原串中出现过,从 \(1\) 往上跳也能遍历到,所以不需要再添加新边了。
读到这里,可能还有一个疑问,为什么要求 \(1\) 的 \(len\) 等于 \(0\) 的 \(len+1\) 呢?这个问题我们将在下面对比解释。
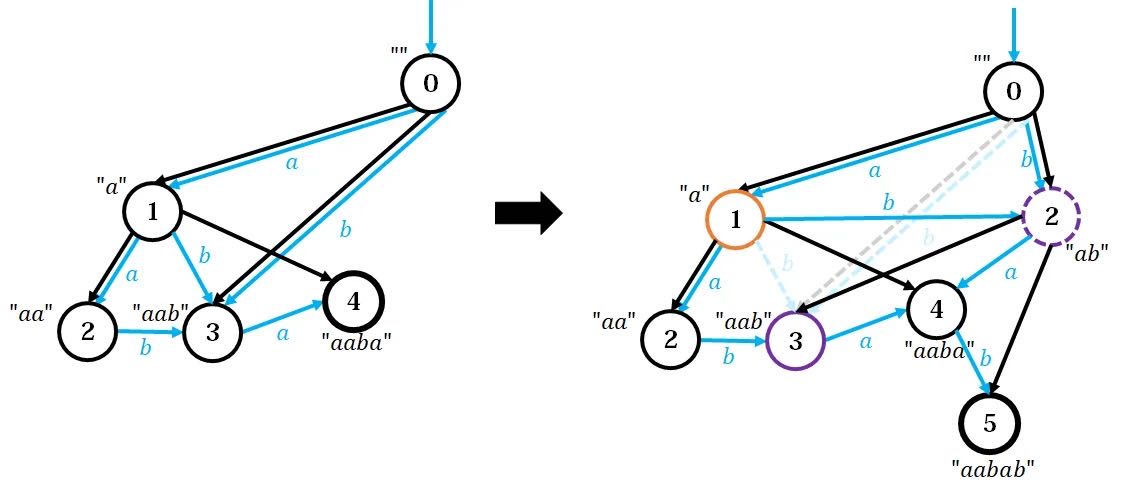
左图为添加 \(\texttt{aaba}\) 后的形态,右图新添加了字符 \(\texttt{b}\)。这次我们不模拟了,直接开始讲解(因为太麻烦了)。
观察左图,找到原串的节点 \(4\),它代表的字符串有 \(\texttt{aaba,aba,ba}\),这些都是原串的后缀,而它们不存在 \(\texttt{b}\) 的出边,即原串中不存在 \(\texttt{aabab,abab,bab}\),所以要连到新点 \(5\) 上。此时新点 \(5\) 表示的字符串有 \(\texttt{aabab,abab,bab}\)。
接着沿着 tree 往上爬,找到节点 \(1\),它代表的字符串为 \(\texttt{a}\)。这个节点存在 \(\texttt{b}\) 的出边,指向 \(3\),这意味着原串中已经存在新串的后缀 \(\texttt{ab}\),且归属节点 \(3\)。
如果我们像上面一样,直接把新点 \(5\) 的 fa 设为 \(3\),即节点 \(3\) 为新串的后缀,就会产生问题: \(3\) 所代表的另一个字符串 \(\texttt{aab}\) 并非新串后缀。
因为,\(3\) 的 \(len\) 并不是 \(1\) 的 \(len+1\),这意味着 \(3\) 代表的最长串并非由 \(1\) 转移而来。如果 \(3\) 表示的某个串比 \(\texttt{ab}\) 更长,则其一定不是新串后缀。这是因为,比 \(\texttt{ab}\) 更长的新串后缀如 \(\texttt{bab}\) 等,已经确定在原串中没有出现,所以才连到了新点 \(5\)。
原来,在原串中 \(\texttt{ab}\) 和 \(\texttt{aab}\) 之所以能共用一个节点 \(3\),是因为历史的局限性,我们以为这两个串是等价的。但加上新字符后,我们发现,\(\texttt{ab}\) 是新串后缀而 \(\texttt{aab}\) 不是,所以这两个必须区分开。为此,我们专门开一个新节点 \(r\),只存这个 \(\texttt{ab}\),而剥夺节点 \(3\) 对 \(\texttt{ab}\) 的占有权。
由于以前这两个等价,所以 \(r\) 应该与节点 \(3\) 有相同的出边,但对于所有原串的更短的后缀 \(x\),如果 \(x\xrightarrow{\texttt{b}}3\),则更改为 \(x\xrightarrow{\texttt{b}}r\)。这是因为,\(x\) 存的一定为 \(\texttt{a}\) 的后缀,添加一个字符 \(\texttt{b}\) 才到 \(\texttt{ab}\),而现在 \(r\) 才是真的 \(\texttt{ab}\),所以要这样连。对于那些连到 \(3:\texttt{aab}\) 的点,如 \(2:\texttt{aa}\),一定不是原串的后缀,不会被更改。
此时,还要将 \(3\) 的 fa 设为 \(r\)(因为 \(r\) 显然是 \(3\) 的后缀),且 \(r\) 的 fa 设为 \(3\) 的原 fa。这样,我们才能在 tree 上正确的遍历这些串的后缀。最后的最后,别忘了将新点的 fa 设为 \(r\)。
现在可以解释第二节最后的问题了:为什么 \(0\) 的 \(len+1\) 等于 \(1\) 的 \(len\),就不需要这么麻烦?因为此时 \(1\) 代表的字符串总共就只有一个,不会出现因历史局限性而混淆两个串的情况,是合法的新串后缀。
完结撒花! 如果有哪些部分没看懂或不清楚,强烈建议先对照图和算法流程模拟一遍,再看我的解析。个人认为绝对能理解(蜜汁自信)
应用
基础应用可以直接看 pecco 大佬的原文,讲得比较明白。这里着重说一下较难理解的最长公共子串。
要求 \(s\) 和 \(t\) 的最长公共子串,可以对 \(s\) 建 SAM,从左到右扫 \(t\) 的每一位,算以这一位结尾的最长公共子串所在的节点。每次新加入一位时,如果可以直接转移则转,如果没有这条转移边,就退而求其次,跳到 fa 节点试图转移(因为 fa 是本质不同的最长后缀),直到有转移边为止。
如果要求 \(s_1,s_2,\cdots,s_n\) 的最长公共子串,可以对 \(s_1\) 建 SAM,把 \(s_2\sim s_n\) 都跑一遍,对每个节点算出跑到这个节点的最短长度(因为要公共子串),最后取 \(\max\)。注意,跑到一个节点相当于也跑到了它的 tree 上的祖先(因为祖先是后缀),所以要树形 DP 更新一遍再统计答案。
更多神仙应用可参见 OI-wiki。
例题
由于作者很菜,所以这里只放链接,就不班门弄斧了。
标签:SAM,sam,后缀,texttt,笔记,学习,fa,len,节点 From: https://www.cnblogs.com/cxm1024/p/17151058.html