本文仅发布于此博客和作者的洛谷博客,不允许任何人以任何形式转载,无论是否标明出处及作者。
一、割点
模板题:link
首先我们先来看看割点这个玩意到底是什么。
在一个无向连通图中,如果删掉某个点和所有连接这个点的边,原图不再连通,那么这个点就是一个割点。
举个例子:
对于这个图,节点3和6就是割点,因为删掉3后4和其他点不连通,删掉6后2和其他点不连通。
可以进行\(O(n^2)\)的sb暴力,不过多进行废话。
我们直接来看作为正解的\(Tarjan\)算法。
为了介绍这个算法,我们需要引入一些名词。
-
dfs序(
dfn[i]):在图中进行dfs的时候,
dfn[i]表示第\(i\)个节点是第几个被遍历到的。还用上面那张图,如果从节点\(1\)开始遍历,从左到右遍历每个孩子,那么
节点编号 \(1\) \(2\) \(3\) \(4\) \(5\) \(6\) dfs序( dfn)\(1\) \(6\) \(4\) \(5\) \(3\) \(2\) 很好理解对罢。
-
树边:
在dfs的时候经过的边。

红色的就是树边 配合dfs序表格理解效果更佳。
-
非树边:
不是树边(没有在dfs中经过)的边就是非树边。
-
low值:
这玩意相对来说就稍微有点变态了。
它的定义是:
“
low[i]表示 节点\(i\)及它的子树中所有点 和 从上述点出发通过一条非树边能到达的点 中最小的dfn.”我们拿张图来看一下。

看到4号点。4号点本身和它的子树中的点都被画成了蓝色(4 5 6 7 8),由这些蓝色点出发,只经过一条非树边,可以到达的点被画成了绿色(2 3 4),经过的非树边也是绿色的。
在这些有颜色的点中,
dfn最小的点(dfn已经被整理成和节点的编号一样)是2,所以low[4]就是2.自己尝试给出
low[11]的值。(
low[11]\(=11\))可以自己再尝试算一下
low[15]和low[9]。(分别为\(11\)和\(9\))
一定要想明白
low是什么东西再继续。
我们先不管dfn和low怎么求 什么的,下面再来看一个牛逼的性质:
对于非根节点,如果一个点的某一个孩子的
low值\(\geq\)这个点的dfn,那么这个点为割点。
为什么?我们可以进行如下十分不严谨的理解:
如果我们把上面那张图里所有的非树边全部刨去,只剩下一棵树,那这棵树就是这个样子的:

比如说,我们删掉点4,那么现在以5为根的那棵子树一定是会和其他部分分离开来。
但是可能有非树边,让下边的部分仍然连着上面。
非树边很多,只画了一条,剩下的不多画了。

就像这个样子。
我们发现,这种让下面连着上面的边一定是一个端点在“以4的儿子为根(此处为5)的子树上”,一个在4的祖先上。
子树上很好理解,为什么一定是在祖先上呢?不能连到别的树上,比如连到点11?
对不起,真不行,因为这棵树是dfs出来的。
想一下,比如说如果9连着11,那为什么dfs到9以后不进一步以\(9\to11\)为树边dfs呢?
所以,像这种的“横叉边”是绝对不可能在这棵dfs树上出现的。
于是,下面连着上面的那种边一定是在4的祖先上的。
而我们又有一个十分显然且好用的性质:
一个点的祖先的dfs序一定比当前点小。
因为遍历肯定是从祖先到儿子遍历的,儿子遍历到了祖先肯定在此之前也被遍历到,所以性质显然成立。
那我们就很明确了,如果找到一条边,上面连着4的祖先,下面挂着5的子树,那么删掉4以后,以5为根的这棵子树就还能继续挂着,4也就不是割点。
这里就有一条\(7\to3\).
不过这里注意,并不是所有的非树边都可以挂上,比如说\(6\to4\),连的是4而不是4的祖先,4删掉以后这条边也没了,还是挂不上去。或者连一条\(7\to5\)(原图中没有),在自己这个子树上连来连去,也是没有任何用的。
我们转回来看一眼low的定义:“low[i]表示节点\(i\)及它的子树中所有点和从上述点出发通过一条非树边能到达的点中最小的dfn.”
如果节点i的所有儿子的low都\(<\)dfn[i],那么它的所有子树在它本身删掉以后还能原封不动挂在主树上面,那么这个点就不是割点。反之,如果有一个儿子的子树挂不上去,那么这个点删掉以后那棵子树就被分开了,图就不再连通,于是这个点就是割点。
这样,我们就得到了上面那个性质:对于非根节点,如果一个点的某一个孩子的low值\(\geq\)这个点的dfn,那么这个点为割点。
不过,对于根节点,我们还需要进行特殊处理。
根节点的dfn最小,没有比它的dfn更小的节点,所以根节点的所有儿子的low一定\(\geq\)dfn,根节点也一定是割点,这显然是荒谬的。
对于根节点,如果子树数量\(\geq2\),那么根节点就是割点,否则不是。证明显然。
现在我们再来看看dfn和low怎么求的问题。
dfn很简单,记录一个cnt,每次遍历一个新的点的时候cnt++并保存一下这个时间戳就是dfn了。
一个点的儿子的子树肯定也是这个点的子树的一部分,从儿子子树往外走一条非树边也就是从这个点的子树往外走一条边。
所以我们尝试递归求解low。每次先dfs它的所有儿子,算出来它们的low,然后low[i]=min(low[i],low[son])即可。(另外如果没有son那么low[i]就等于dfn[i])
不过,在dfs完儿子以后,也要从自己往外走一条非树边(如果有),low[i]=min(low[i],dfn[to]).
这样我们的low就更新出来了。
还有一堆细节没有说,但是因为比较繁琐就直接扔进代码注释里面了。
#include<bits/stdc++.h>
using namespace std;
vector<int> g[100005];//邻接表
int dfn[100005];
int low[100005];
int fa[100005];//记录一个点的父亲
bool cut[100005];
int cnt=0;
void tarjan(int k,int root){//k是当前点,root是这个子图的根节点
int child=0;//k=root时专属,判断root是不是割点用的
cnt++;//时间戳
dfn[k]=cnt;
low[k]=cnt;//同dfn,low初始赋值为cnt.
for(int i=0;i<g[k].size();i++){//进行一个对所有子树的遍历
if(g[k][i]==fa[k]){//显然不能遍历到父亲节点上。
/*
有人直接把判父亲的这段直接不要了,也是没什么问题的,此时low的意义发生了一点轻微的改变。
但是为了严谨一点还是加上罢 反正多两行又死不了(划掉
*/
continue;
}
if(dfn[g[k][i]]==0){//这里表示找到了一个新点
if(k==root){//k=root专属,root的儿子++
child++;
}
fa[g[k][i]]=k;
tarjan(g[k][i],root);//把过来的这条边整成树边,遍历这个儿子
low[k]=min(low[k],low[g[k][i]]);//更新当前low
if(k!=root&&low[g[k][i]]>=dfn[k]){//如果它的儿子的low比自己的dfn大,那么自己是割点。
cut[k]=true;//mark一下
}
}else{//不写else也没问题,具体实现还是很宽松的。
//找到的点之前来过,代表这是一条非树边
low[k]=min(low[k],dfn[g[k][i]]);//走非树边
}
}
if(k==root&&child>1){//判断root是不是割点
cut[k]=true;
}
}
int main(){
int n,m;
int tmpa,tmpb;
cin>>n>>m;
for(int i=1;i<=m;i++){//存边
cin>>tmpa>>tmpb;
g[tmpa].push_back(tmpb);
g[tmpb].push_back(tmpa);
}
for(int i=1;i<=n;i++){//割点要求必须是无向连通图,但是题目并没有保证。显然题目的意思是求出每一个连通子图里的割点。
if(dfn[i]==0){//意思是当前节点还没遍历到,这里就是一个全新的子图。
tarjan(i,i);
}
}
int sum=0;
for(int i=1;i<=n;i++){
if(cut[i]){
sum++;
}
}
cout<<sum<<endl;//先输出总数再输出具体id
for(int i=1;i<=n;i++){
if(cut[i]){
cout<<i<<' ';
}
}
return 0;
}
我们的割点终于就大功告成了...
二、割边
先看一下割边是什么。
割边的定义和割点类似,不过更好理解:在无向连通图中如果有一条边,删掉后图变成非连通图,那么这条边就是割边。
人话就是砍掉以后图裂开成两半的边。
举个例子理解一下。
9 11
1 2
2 3
3 4
4 5
5 6
3 5
4 6
5 7
7 8
8 9
7 9

显然,三个割边分别为\(7\to5\),\(3\to2\),\(1\to2\).原因显然。
显然,和割点一样,如果一个点某个儿子的low\(>\)这个点的dfn,那么儿子到这个点的这条边是割边。(子树挂不上主树)
\(<\)dfn的情况呢?

同割点,可以挂上。
\(=\)呢?

和割点不一样,可以挂上,不是割边。
由此,我们总结出割边的判断方法:
如果一个点的某个孩子的
low\(>\)
这个点的dfn,那么这个孩子到这个点的边是割边。
我们发现和割点的判断方法只有两点不同。
-
\(\geq\)变成了\(>\),\(=\)时不是割边。
-
“对于非根节点”没了。
第一条上面解释过了,第二条比较显然,根节点也能用。
所以,我们的割边就圆满结束了,最后和割点的核心区别也只有少了一个等于号,砍掉了算子树的部分而已。
#include<bits/stdc++.h>
using namespace std;
vector<int> g[100005];
vector<bool> bridge[100005];//记录一条边是不是割边
int dfn[100005];
int low[100005];
int fa[100005];//记录一个点的父亲
int cnt=0;
void tarjan(int k){
cnt++;
dfn[k]=cnt;
low[k]=cnt;
for(int i=0;i<g[k].size();i++){
if(g[k][i]==fa[k]){
continue;
}
if(dfn[g[k][i]]==0){
fa[g[k][i]]=k;
tarjan(g[k][i]);
low[k]=min(low[k],low[g[k][i]]);
if(low[g[k][i]]>dfn[k]){//如果是割边就记录。注意是>不是>=
bridge[k][i]=true;
}
}else{
low[k]=min(low[k],dfn[g[k][i]]);
}
}
//没有烦人的什么根节点什么的 很清爽
}
int main(){
int n,m;
int tmpa,tmpb;
cin>>n>>m;
for(int i=1;i<=m;i++){
cin>>tmpa>>tmpb;
g[tmpa].push_back(tmpb);
g[tmpb].push_back(tmpa);
bridge[tmpa].push_back(false);
bridge[tmpb].push_back(false);//这个bridge写的很丑。。但是能跑 就行
}
for(int i=1;i<=n;i++){
if(dfn[i]==0){
tarjan(i);
}
}
int sum=0;
for(int i=1;i<=n;i++){
for(int j=0;j<bridge[i].size();j++){
if(bridge[i][j]==true){
sum++;
}
}
}
cout<<sum<<endl;
for(int i=1;i<=n;i++){
for(int j=0;j<bridge[i].size();j++){
if(bridge[i][j]==true){
cout<<i<<' '<<g[i][j]<<endl;
}
}
}
return 0;
}
可惜没有模板题...这份代码我们后面还要用 原封不动完全不带改的那种。
三、点双连通分量
定义点双连通图为“不存在任何割点的无向连通图”。
则一个无向图中的点双连通分量为“极大”的点双连通子图。
“极大”的意思是“不管往这个点双连通子图里面加多少点,加什么点,都会让这个子图不再是点双连通子图”。
人话其实就是尽可能的大啦。
注意,一个图里可以(甚至绝大部分都)有很多点双连通分量(以下就简称点双了)。
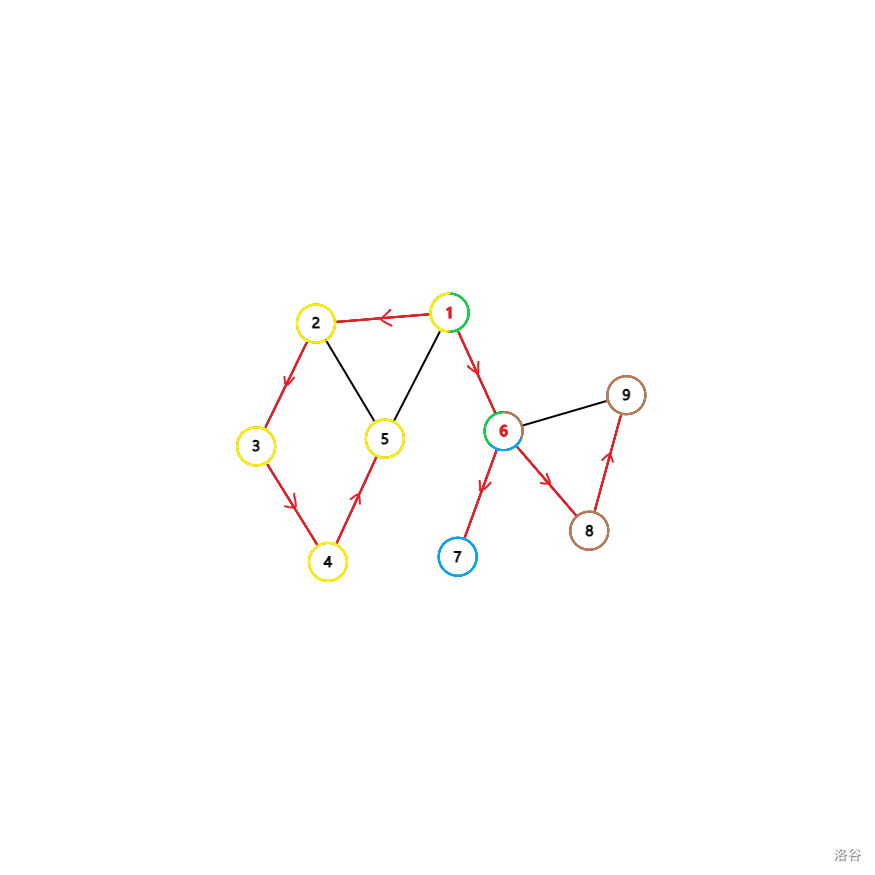
上图中,一个颜色的是一个点双,可以发现割点\(1\),\(6\)(标红)同时属于多个点双。
我们先来证几个东西。
- 只有割点会同时在多个点双中。

如图,如果1不是割点,那删掉1后,两个点双依旧连通。所以,两个点双之间就有两条连通的路径了(一条是绿边,还有一条经过1)。此时两个点双合并起来还是点双,不符合“极大”的定义。
- 对于一个点双,如果某个非根节点的父亲节点不在这个点双中,那这个点一定是割点。
由割点性质,如果这个点不是割点,那一定有一条非树边可以返回到父亲节点或父亲节点的祖先。这样,就能通过那条非树边找到一个环,包含父亲和它本身。这个环显然是点双连通子图。根据“极大”的定义,这个点双连通子图一定被一个点双连通分量完全包含,所以得证。
- 一个点双在dfs中最先被遍历到的一定是割点或树根。
根据2,可知一个点双最靠上的点一定是割点或树根,其他点都在它的子树中。所以dfs时想要遍历到其他点必须先经过割点/树根,割点/树根一定是最先遍历到的,得证。
由1,2,我们可以把一个点双看做“在一个割点上生长出来的”,来更容易地理解这个算法。

从根节点开始生长,每到一个割点就会被截断一部分(或全部),在割点的基础上生长出新的点双。
算法的过程是从下往上遍历,每找到一个割点和“删掉这个点就不和图连通”的儿子,就代表在这个割点上,往这个儿子的方向生长出了一个点双。在图中删除掉儿子的子树(把新生的点双去掉),继续往上遍历。
在实际情况中,我们会用stack记录经过的点,来更方便地进行删除子树的操作(弹栈即可)。
实际情况(模板题)中,可能会有重边自环,注意处理即可。
#include<bits/stdc++.h>
using namespace std;
vector<int> g[500005];
int dfn[500005];
int low[500005];
int fa[500005];
vector<int> dcc[500005];//存点双
stack<int> s;
int cnt=0;
int sum=0;//点双总数
int n,m;
bool isolated(int k){//判断当前节点是否为孤立节点
for(int i=0;i<g[k].size();i++){
if(g[k][i]!=k){
return false;
}
}
return true;//连出来的边全是自环||根本没边
}
void tarjan(int k){
cnt++;
dfn[k]=cnt;
low[k]=cnt;
if(isolated(k)){//孤立节点直接单独成一个点双
sum++;
dcc[sum].push_back(k);
return;
}
s.push(k);//当前节点push进去
for(int i=0;i<g[k].size();i++){
if(g[k][i]==fa[k]){
continue;
}
if(dfn[g[k][i]]==0){
fa[g[k][i]]=k;
tarjan(g[k][i]);
low[k]=min(low[k],low[g[k][i]]);
if(low[g[k][i]]>=dfn[k]){//找到割点
sum++;
while(s.top()!=g[k][i]){//断掉的割点儿子的子树中的所有点全部扔掉
dcc[sum].push_back(s.top());
s.pop();
}
dcc[sum].push_back(g[k][i]);//没删干净,把那个割点儿子也扔进去
s.pop();
dcc[sum].push_back(k);//割点本身也push进去但是不删
}
}else{
low[k]=min(low[k],dfn[g[k][i]]);
}
}
}
int main(){
cin>>n>>m;
int t1,t2;
for(int i=1;i<=m;i++){
cin>>t1>>t2;
g[t1].push_back(t2);
g[t2].push_back(t1);
}
for(int i=1;i<=n;i++){
if(dfn[i]==0){
while(!s.empty()){//stack可能没清干净
s.pop();
}
tarjan(i);
}
}
cout<<sum<<endl;
for(int i=1;i<=sum;i++){
cout<<dcc[i].size()<<' ';
for(int j=0;j<dcc[i].size();j++){
cout<<dcc[i][j]<<' ';
}
cout<<endl;
}
return 0;
}
四、边双连通分量
咕咕咕咕
五、强连通分量
咕咕咕咕咕
标签:Tarjan,Unfinished,连通,int,割点,dfn,low,节点 From: https://www.cnblogs.com/CerebralFissure/p/Tarjan.html