网络最大流学习笔记
形式化的定义
网络流问题是指:
给定一张有向图(称之为网络) \(G(V, E)\), 每条边都有一个权值(称之为容量) \(c(u,v)\), 对于 \((u,v)\notin E\) 有 \(c(u,v)=0\)
定义两个特殊的点:源点 \(s\in V\) 和 汇点 \(t\in V\) \((s\ne t)\)
设 \(f(u,v)\) 定义在二元组 \((u\in V,v\in V)\) 上的实数函数且满足
\[f(u,v)=\left\{ \begin{aligned} &f(u,v),&(u,v)\in E\\ &-f(v,u),&(v,u)\in E\\ &0,&(u,v)\notin E,(v,u)\notin E \end{aligned}\right. \]容易发现其满足如下的性质:
- 容量限制:对于每条边,流经该边的流量不得超过该边的容量,即,\(f(u,v)\leq c(u,v)\)
- 斜对称性:每条边的流量与其相反边的流量之和为 0,即 \(f(u,v)=-f(v,u)\)
- 流守恒性:从源点流出的流量等于汇点流入的流量,即 \(\forall x\in V-\{s,t\},\sum_{(u,x)\in E}f(u,x)=\sum_{(x,v)\in E}f(x,v)\)
那么 \(f\) 称为网络 \(G\) 的流函数。对于 \((u,v)\in E\),\(f(u,v)\) 称为边的 流量,\(c(u,v)-f(u,v)\) 称为边的 剩余容量。整个网络的流量为 \(\sum_{(s,v)\in E}f(s,v)\),即 从源点发出的所有流量之和。
通常而言, 要求的流量指的是 整个网络的流量
通俗理解
通俗的讲, 可以把流理解为水流, 边理解为水管, 源点为水池, 汇点为水龙头, 水管有粗有戏, 问最多能流出多少水。
网络最大流的求解
网络最大流的常见求解方法都是基于 反悔贪心, 具体地说, 贪心地进行流, 然后利用一条 反向边 用来 抵消 先前流过的流量, 相当于是抵消了先前错误的决定
Ford-Fulkerson
通常来说, 在求解网络流的过程中, 每次在图上找到一条路径, 满足:路径上所有边剩余流量都 \(> 0\)(称之为增广路) ,然后找到这条路径上边权最小的边(限制这一条路径能流的流量的边), 把这条路径上所有边的实际流量都加上这一条边的流量, 再把这条边上所有反边的实际流量都扣除掉这一条边的流量(等价于 \(c(u,v)\) 的增加, 可以用来反悔)
OI-wiki上的一个例子
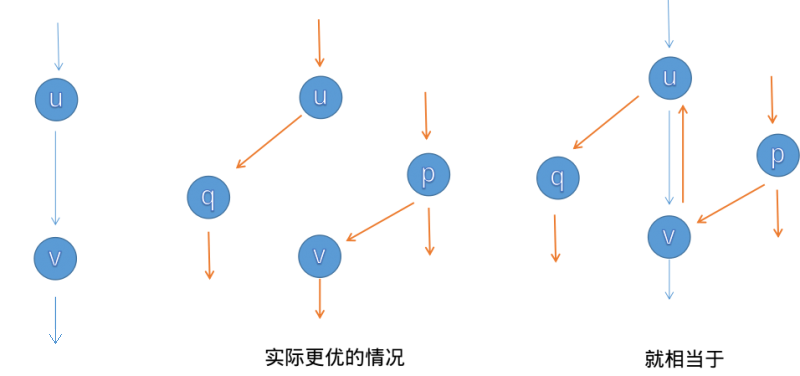
第一次走时, 给 \((u,v)\) 增加了流量, 给 \((v,u)\) 扣除了流量(剩余流量增加), 那么从 \(p\) 再流时可以 \(v\) 回流一部分(或者如图中,全部回流)到 \(u\), 抵消掉 \(u\) 不需要贡献给 \(v\) 的流量, 再从 \(u\) 流去其他节点, 这等价于从 \(u\) 直接流出到其他节点
如果直接暴力 DFS 找最大流, 时间复杂度为 \(O(|E||f|)\) 其中 \(|f|\) 为图中的最大流, 因为每轮增广流量单调递增, 所以最多有 \(|f|\) 次增广, 单轮增广最坏 \(O(|E|)\), 这个复杂度很坏, 但是可以在这个求最大流的思想上对其继续优化。
Dinic
网络流卡 Dinic 的出题人都有才无德
Dinic 利用 BFS 分层和 DFS 找增广路保证复杂度, 具体地说, 在每次 DFS 找增广路之前先利用 BFS 给图分层, 保证 DFS 不会走回头路, 随后把找出来的新流并入原来的流中, 持续找增广路直到无路可走为止
注意到如果一个点的度数很大, 那可能需要枚举每一条边来判断是否需要流出流量, 对此我们可以引入当前弧优化——所有流满的边都不需要流, 那么维护第一条还需要流的边即可
示例代码如下
#include <bits/stdc++.h>
using namespace std;
const int N = 250, M = 1e4 + 1000;
const long long INF = 0x3f3f3f3f;
int n, m, s, t;
int idx = 0, h[N], e[M], ne[M];
//w:存的是这条边的最大流量
long long w[M];
inline void add(int a, int b, long long c){
e[idx] = b, ne[idx] = h[a], w[idx] = c, h[a] = idx++;
}
//now:当前弧 dep:点的深度(分层图)
int now[N], dep[N];
bool bfs(){
//每次都初始化深度
memset(dep, 0x3f, sizeof dep);
dep[s] = 0;
now[s] = h[s];
queue<int> Q;
Q.push(s);
while (!Q.empty()) {
int u = Q.front();
Q.pop();
for (int i = h[u]; ~i; i = ne[i]) {
int v = e[i];
//当前弧优化
if (w[i] > 0 && dep[v] == INF) {
Q.push(v);
now[v] = h[v];
dep[v] = dep[u] + 1;
//在所有流量非空的边连起来的图里还能找到终点, 也就是还能再流
if (v == t)
return true;
}
}
}
return false;
}
int dfs(int u, long long maxflow){
//流到头了或者流不出了就返回
if (u == t || !maxflow)
return maxflow;
//flow 是当前这个点的流量
long long k = 0, flow = 0;
for (int i = now[u]; ~i && maxflow > 0; i = ne[i]) {
now[u] = i;
int v = e[i];
if (w[i] > 0 && (dep[v] == dep[u] + 1)) {
//当前点能流出的最多流量与这条边能承受的流量取min
k = dfs(v, min(maxflow, (long long)w[i]));
if (k == 0)
dep[v] = INF;
//在这条边上增加流量, 相当于在c(u,v)上扣除流量
w[i] -= k;
//i ^ 1是反边, 同上
w[i ^ 1] += k;
flow += k;
//maxflow是这个点还能流出的最大流量
maxflow -= k;
if(!maxflow)
break;
}
}
return flow;
}
int main()
{
memset(h, -1, sizeof h);
scanf("%d%d%d%d", &n, &m, &s, &t);
for (int i = 1; i <= m; i++) {
int a, b;
long long c;
scanf("%d%d%lld", &a, &b, &c);
//一个技巧:正边编号偶数, 反边编号奇数, 那么任何一条边编号 xor 1 都是自己的反边
//反边的初始流量为 0
add(a, b, c), add(b, a, 0);
}
long long ans = 0;
while (bfs()) {
ans += dfs(s, INF);
}
printf("%lld\n", ans);
return 0;
}
时间复杂度分析
Dinic 在一般图上的复杂度最坏为 \(O(|V|^2|E|)\) 然而极其难卡
在二分图上的复杂度是 \(O(\sqrt{|V|} |E|)\), 如果所有边流量都为 \(1\), 复杂度为 \(O(|E|\min(|E|^{\frac{1}{2}}, |V|\sqrt|V|))\)
参见 OI-wiki上的Dinic复杂度分析