前缀和-差分-双指针（上）

标签：25 前缀 nums 差分 let 数组 10 指针

1.前缀和

• 前n个元素的和作为当前元素的值
• a 为元素数组 s[i] 为前缀和数组
• 一维前缀和
  • s[i]=s[i-1]+a[i]
  • s[m]-s[n]=a[n+1]+...+a[m] m>n
• 二维前缀和
  • s[i][j]=s[i-1][j]+s[i][j-1]-s[i-1][j-1]+a[i][j]

LeetCode

1248. 统计「优美子数组」

给你一个整数数组 nums 和一个整数 k。如果某个连续子数组中恰好有 k 个奇数数字，我们就认为这个子数组是「优美子数组」。

请返回这个数组中 「优美子数组」 的数目。

示例 1：

输入：num
s = [1,1,2,1,1], k = 3
输出：2
解释：包含 3 个奇数的子数组是 [1,1,2,1] 和 [1,2,1,1] 。

示例 2：

输入：nums = [2,4,6], k = 1
输出：0
解释：数列中不包含任何奇数，所以不存在优美子数组。

示例 3：

输入：nums = [2,2,2,1,2,2,1,2,2,2], k = 2
输出：16

提示：

• 1 <= nums.length <= 50000
• 1 <= nums[i] <= 10^5
• 1 <= k <= nums.length

完整代码

/**
 * @param {number[]} nums
 * @param {number} k
 * @return {number}
 */
var numberOfSubarrays = function(nums, k) {

    // 解题思路

    // 连续子数组恰有k个奇数数字
    // 我们把偶数置为0，奇数置为1
    // 问题转换为连续子数组的和为k

    // 转换为前缀和 即s[i]-s[j]=k
    // 即s[j]=s[i]-k  ==> s[j]>=0   ==>s[i]-k>=0

    // s[i]-k 其实是前缀和s[j]   那么这样的s[j]有多少个呢 即统计s[j] 的count

    // 转换数组并计算前缀和

    // 定义一个count数组，通过s[j]的个数
    let count=new Array(nums.length+1).fill(0)
    count[0]=1
    let s=new Array(nums.length+1).fill(0)
    for(let i=0;i<nums.length;i++){
        nums[i]=nums[i]%2
        s[i+1]=s[i]+nums[i]
        count[s[i+1]]++
    }

    console.log(s)

    let res=0
    for(let i=1;i<nums.length+1;i++){
        if(s[i]-k>=0){
            res+=count[s[i]-k]
        }
    }

    return res

};

304. 二维区域和检索 - 矩阵不可变（模板题）

给定一个二维矩阵 matrix，以下类型的多个请求：

• 计算其子矩形范围内元素的总和，该子矩阵的 左上角 为 (row1, col1) ，右下角 为 (row2, col2) 。

实现 NumMatrix 类：

• NumMatrix(int[][] matrix) 给定整数矩阵 matrix 进行初始化
• int sumRegion(int row1, int col1, int row2, int col2) 返回 左上角 (row1, col1) 、右下角 (row2, col2) 所描述的子矩阵的元素 总和 。

示例 1：

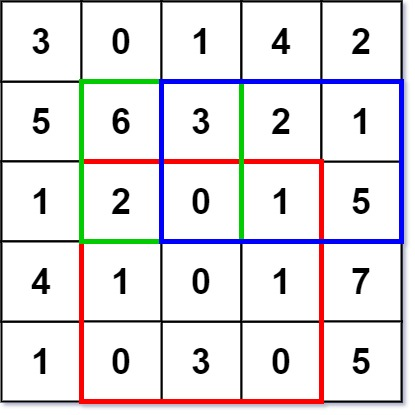
输入: 
["NumMatrix","sumRegion","sumRegion","sumRegion"]
[[[[3,0,1,4,2],[5,6,3,2,1],[1,2,0,1,5],[4,1,0,1,7],[1,0,3,0,5]]],[2,1,4,3],[1,1,2,2],[1,2,2,4]]
输出: 
[null, 8, 11, 12]

解释:
NumMatrix numMatrix = new NumMatrix([[3,0,1,4,2],[5,6,3,2,1],[1,2,0,1,5],[4,1,0,1,7],[1,0,3,0,5]]);
numMatrix.sumRegion(2, 1, 4, 3); // return 8 (红色矩形框的元素总和)
numMatrix.sumRegion(1, 1, 2, 2); // return 11 (绿色矩形框的元素总和)
numMatrix.sumRegion(1, 2, 2, 4); // return 12 (蓝色矩形框的元素总和)

提示：

• m == matrix.length
• n == matrix[i].length
• 1 <= m, n <= 200
• -105 <= matrix[i][j] <= 105
• 0 <= row1 <= row2 < m
• 0 <= col1 <= col2 < n
• 最多调用 104 次 sumRegion 方法

解题思路

1. 二维前缀和
2. 面积计算，计算阴影面积一样，

完整代码

/**
 * @param {number[][]} matrix
 */
var NumMatrix = function(matrix) {

    // 生成二维前缀和矩阵
    let m=matrix.length
    let n=matrix[0].length
    // this.sums=new Array(m+1).fill(new Array(n+1).fill(0))

    this.sums = new Array(m + 1).fill(0).map(() => new Array(n + 1).fill(0));

    // console.log(this.sums)
    // console.log(matrix)
    
    // 生成二维前缀和
    for(let i=0;i<m;i++){
        for(let j=0;j<n;j++){
            this.sums[i+1][j+1]=this.sums[i][j+1]+this.sums[i+1][j]-this.sums[i][j]+matrix[i][j]
        }
    }

    // console.log(this.sums[0][1])

};

/** 
 * @param {number} row1 
 * @param {number} col1 
 * @param {number} row2 
 * @param {number} col2
 * @return {number}
 */
NumMatrix.prototype.sumRegion = function(row1, col1, row2, col2) {
    // console.log(this.sums)

    // 计算阴影面积
    return this.sums[row2+1][col2+1]-this.sums[row1][col2+1]-this.sums[row2+1][col1]+this.sums[row1][col1]
};

/**
 * Your NumMatrix object will be instantiated and called as such:
 * var obj = new NumMatrix(matrix)
 * var param_1 = obj.sumRegion(row1,col1,row2,col2)
 */

2.差分

• 原数组A

  • [1,2,1,3,2]

• 差分数组B，b[1]=a[1] , b[i]=a[i]-a[i-1]

  • [1,1,-1,2,-1]

• 性质

  • 差分数组B的前缀和数组为原数组A
  • 将原数组m-n之间的元素+d，对应的差分数组B，B[m]+d，B[n+1]+d

LeetCode

1109. 航班预订统计

这里有 n 个航班，它们分别从 1 到 n 进行编号。

有一份航班预订表 bookings ，表中第 i 条预订记录 bookings[i] = [firsti, lasti, seatsi] 意味着在从 firsti 到 lasti （包含 firsti 和 lasti ）的 每个航班 上预订了 seatsi 个座位。

请你返回一个长度为 n 的数组 answer，里面的元素是每个航班预定的座位总数。

示例 1：

输入：bookings = [[1,2,10],[2,3,20],[2,5,25]], n = 5
输出：[10,55,45,25,25]
解释：
航班编号        1   2   3   4   5
预订记录 1 ：   10  10
预订记录 2 ：       20  20
预订记录 3 ：       25  25  25  25
总座位数：      10  55  45  25  25
因此，answer = [10,55,45,25,25]

示例 2：

输入：bookings = [[1,2,10],[2,2,15]], n = 2
输出：[10,25]
解释：
航班编号        1   2
预订记录 1 ：   10  10
预订记录 2 ：       15
总座位数：      10  25
因此，answer = [10,25]

提示：

• 1 <= n <= 2 * 104
• 1 <= bookings.length <= 2 * 104
• bookings[i].length == 3
• 1 <= firsti <= lasti <= n
• 1 <= seatsi <= 104

解题思路

1. 如果使用朴素算法，则需要遍历k*n次 k为预定记录数，n为每条记录预定的航班（超时）
2. 使用差分，因为我们发现每个预定记录k，预定的航班是连续的，且票数相同，其实我们只需要算首尾就行了
   时间复杂度2*k

完整代码

/**
 * @param {number[][]} bookings
 * @param {number} n
 * @return {number[]}
 */
var corpFlightBookings = function(bookings, n) {

    // 使用差分数组

    // 原数组 都为0，差分数组也是都为0
    let b=new Array(n+2).fill(0)

    // m到n加上一个数，差分数组b[m]+数 b[n+1]-数

    bookings.forEach(item=>{
        b[item[0]]+=item[2]
        b[item[1]+1]-=item[2]
    })

    // 得到b的前缀和数组，即可以得到原数组

    let s=new Array(n+1)
    s[0]=0
    for(let i=1;i<b.length-1;i++){
        s[i]=s[i-1]+b[i]
    }

    return s.slice(1)


};

53. 最大子数组和

给你一个整数数组 nums ，请你找出一个具有最大和的连续子数组（子数组最少包含一个元素），返回其最大和。

子数组 是数组中的一个连续部分。

示例 1：

输入：nums = [-2,1,-3,4,-1,2,1,-5,4]
输出：6
解释：连续子数组 [4,-1,2,1] 的和最大，为 6 。

示例 2：

输入：nums = [1]
输出：1

示例 3：

输入：nums = [5,4,-1,7,8]
输出：23

提示：

• 1 <= nums.length <= 105
• -104 <= nums[i] <= 104

进阶：如果你已经实现复杂度为 O(n) 的解法，尝试使用更为精妙的 分治法 求解。

完整代码

/**
 * @param {number[]} nums
 * @return {number}
 */
var maxSubArray = function(nums) {

    // 解题思路

    // 即求 a[m]+a[m+1]+....+a[n] 为最大

    // 一般遇到这么的，转换为s[n]-s[m-1]

    // 所以我们先求出前缀和数组
    let s=new Array(nums.length+1).fill(0)
    s[0]=0
    for(let i=0;i<nums.length;i++){
        s[i+1]=s[i]+nums[i]
    }

    // 问题已经转换为s[n]-s[m] 为最大
    // 即在n不变的情况下，寻找s[m]为最小 且m<n ,即前缀和s[m]最小
    // 先求前缀最小值，sMin(5) 前5个元素最小和

    let sMin=new Array(nums.length+1).fill(0)
    sMin[0]=0
    for(let i=0;i<nums.length;i++){
        sMin[i+1]=Math.min(sMin[i],s[i+1])
    }


    // 回归问题，求满足s[i]-s[j] 为 最大的s[j],即s[j]最小，且j<i

    // 而前缀最小和sMin[j] 即为s[j] 最小

    let res=-Infinity
    for(let i=1;i<nums.length+1;i++){
        res=Math.max(res,s[i]-sMin[i-1])
    }

    return res
};

标签：25,前缀,nums,差分,let,数组,10,指针
From： https://www.cnblogs.com/lingxin1123/p/17087586.html