Codeforces Round #818 (Div. 2) D

标签：res ll Codeforces 818 左边 fac Div inv mod

 

 

D：

题意： 由2^n个人进行锦标赛，编号1~2^n，每一场输的人失去比赛资格，赢的人继续。你可以选择他们进行的顺序，以及决定哪一边赢得比赛。你的目标是尽量让编号小的人赢得最终比赛。主办方可以改变其中至多k场比赛的结果，即本来是左边赢改为右边赢，本来是右边赢的改为左边。如下图，最左边红线是你选择的胜方。而主办方改动左边的一个结果，使得最终赢的人变成3。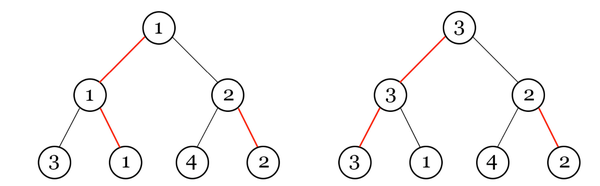 问题是，求一个最小的编号，使得主办方无论怎么改，都可以让他赢。主办方的目的是使编号尽可能大的人赢。

分析：

 

杨辉三角最后一排的和刚好是2^n，也就是最后一排刚好有2^n 个人，杨辉三角，从左往右数，每个位置i ，代表这个位置经过 i 次修改后可以获胜，且这个数的右上角的数是上一层经过 i 次修改可以获胜的数，所以这一层的这一个数在杨辉三角中也代表经过刚好 i 次修改，整个杨辉三角中可以获胜的数的总和。

首先让最左边的人赢，我们让编号小的人尽量在左边，这样如果主办方仅修改一次，左边一侧的1的右边一个会刚好获胜，修改两次，右边第二个刚好会获胜，所以修改k次后会获得胜利的数直接通过累加最后一排的k个数即可

 

 答案就是 s

//#define int ll
const int N = 2e5+10,mod = 1e9+7;
int n,k;

int fac[N],inv[N];

ll qmi(ll a,ll b) {
    ll res = 1;for(;b;b>>=1,a = a * a % mod) if(b&1) res = res * a % mod;return res;
}

ll mul(ll a,ll b) {
    return (a * b) % mod;
}

void init() {
    fac[0] = 1;
    fo(i,1,2e5) fac[i] = (1ll * fac[i-1] * i) % mod;//记得要开ll
    inv[200000] = qmi(fac[200000],mod - 2);
    of(i,2e5,1) inv[i-1] = mul(inv[i],i);
}

ll C(ll n,ll m) {
    if(n < m || m < 0) return 0;
    return mul(fac[n],mul(inv[m],inv[n-m]));
}

void solve()
{
    cin>>n>>k;
    ll res = 0;
//    fo(i,0,10) {
//        dbb(i,fac[i]);
//    }
//    db(C(1,1));
    fo(i,0,(min(k,n))) 
    {
        
        res += C(n,i);
        res %= mod;
    } 
    cout<<res<<endl;
}

 

 

标签：res,ll,Codeforces,818,左边,fac,Div,inv,mod
From： https://www.cnblogs.com/er007/p/16653787.html