链式前向星

注意到邻接矩阵空间复杂度为 \(n^2\) ,查找边复杂化为 \(O(n)\),这在处理数据较大的时候是极其不利好的,我们需要考虑优化.

注意到实际上邻接矩阵存在许多空间的浪费,因为他把所有的边的关系都存入了数组,不过是否相连.如果我们只记录边和边的关系,这样不但 空间是 \(m\),且时间复杂度近似 \(O(1)\) .

想一想,有没有什么数据结构是可以存边的,且不限长度的?你或许会说 \(vector\),这的确是个方法,但是如果不开 \(O2\) 的话,会非常的慢.不妨考虑链表.我们对每一条边都表个号(我无法保证我会连续读入同一点的边),用 \(head_{tot}\) 表示连的下一条边的编号即可,我们知道的编号,就还可以维护其他信息,比如长度这种.

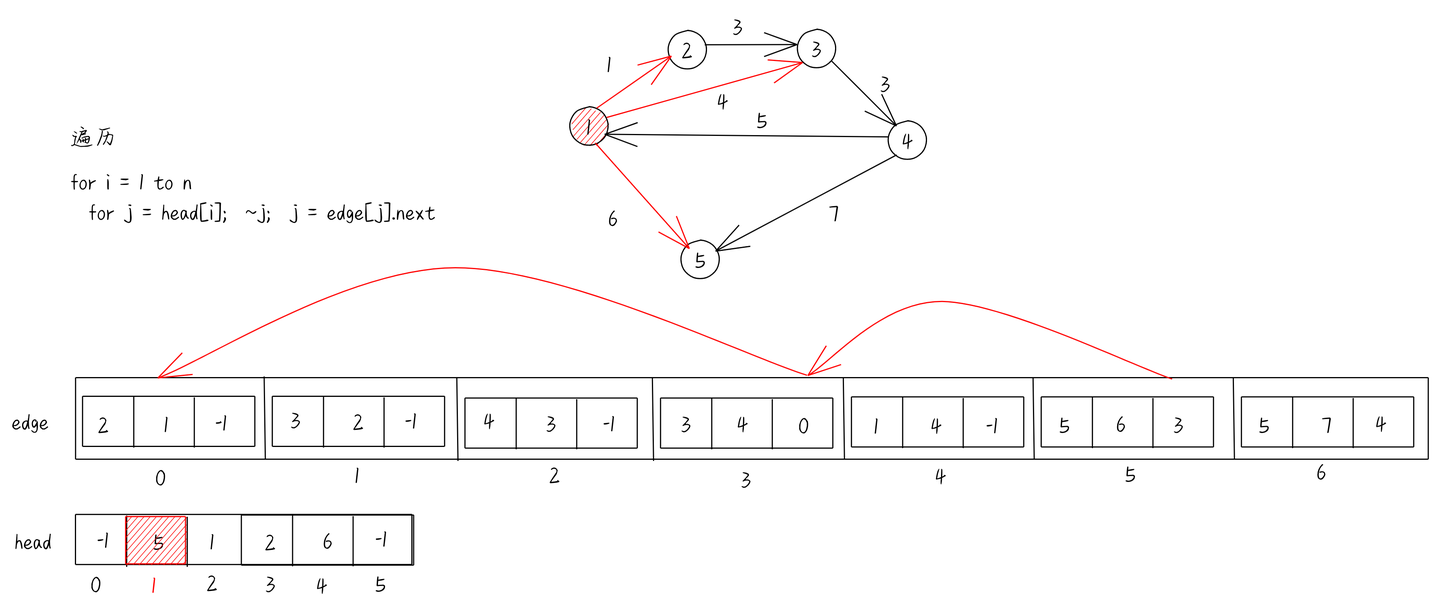
代码如下:

	inline void AddEdge(int u,int v,int w1=0){
    	to[++tot]=v;
      	nxt[tot]=head[u];
      	head[u]=tot;
  	
    }