权值线段树详解

标签：le int 线段 leq 详解 权值 节点

前言

首先明确，权值线段树是线段树的一个子集。它的思想与线段树一模一样，只是实现的功能更加神奇。

前置知识：

• 线段树
• 树状数组

本文将介绍权值线段树、可持久化权值线段树、树状数组套可持久化权值线段树。

权值数组

对于一个序列 \(a\)，若它的权值数组 \(b\)，则：

\[\forall i\in\mathbb{Z},b_i=\sum_{j=1}^{|a|}{[a_j=i]} \]

即 \(b_i\) 为 \(i\) 在 \(a\) 中的出现次数。

我们可以使用线段树来维护权值数组，该线段树便称为权值线段树。

注意 \(b\) 的大小与值域有关，可能特别大，但中的非 \(0\) 值分布十分稀疏（最多 \(|a|\) 个）。我们可以使用下面的方法解决：

• 使用离线 + 离散化将 \(b\) 的大小缩减到 \(|a|\) 级别。
• 使用动态开点线段树来维护。如果值域有负数我们可以使用加上偏移值实现。

权值线段树实现平衡树

概述

实现平衡树的功能（所有操作 \(O(\log n)\)）是权值线段树的基本应用（据说还可以实现文艺平衡树，可是我不会）。

这里我们使用动态开点线段树来维护权值数组。

定义的一些东西：

#define ls (t[i].l) // 左子节点
#define rs (t[i].r) // 右子节点
#define mid ((l+r)>>1) // 区间中部

const int N = 1e5+5;
const int MOV = 1e7; // 值域，也就是偏移值

struct node{// 线段树节点结构体
    int v,l,r;
} t[N<<4];
int tot,root;// tot:节点个数，root：根节点

inline void newnode(int &i){// 如果该节点还没有创建，新建节点
    if(!i) i=(++tot);
}

插入 / 删除

考虑插入对权值数组 \(b\) 的贡献：

• 插入 \(i\)：\(b_i=b_i+1\)
• 删除 \(i\)：\(b_i=b_i-1=b_i+(-1)\)。

于是我们可以写一个线段树的单点修改来实现：

void update(int p,int v,int &i,int l,int r){
    // p:插入的值 v: 1为插入 -1为删除
    newnode(i);
    t[i].v+=v;// 注意到权值线段树经过的地方都会带来贡献，因此我们可以在这里就加上，以后就不用写 pushup 了
    if(l==r){
        if(t[i].v<0) t[i].v=0;// 防止删除不存在的元素
        return; 
    }
    if(p<=mid) update(p,v,ls,l,mid);
    else update(p,v,rs,mid+1,r);
}

查询元素排名

解决这个问题之前，先想想权值数组的前缀和 \(b\) 的意义：

\(\sum_{i=1}^{k}{b_i}\) 为原序列中小于等于 \(k\) 的元素个数。

于是我们想到，\(k\) 的排名其实就是小于 \(k\) 的元素个数加 \(1\)，也就是：

\[(\sum_{i=1}^{k-1}{b_i})+1 \]

可以使用线段树的区间查询（元素和）实现。

int rnk(int ql,int qr,int &i,int l,int r){
    if(!i) return 0;// 如果访问到不存在的节点，直接返回0（不会造成贡献）
    if(ql<=l&&r<=qr) return t[i].v;
    int ans=0;
    if(ql<=mid) ans+=rnk(ql,qr,ls,l,mid);
    if(qr>mid) ans+=rnk(ql,qr,rs,mid+1,r);
    return ans;
}
// 这里只写了区间查询。不过区间查询都实现了查询元素排名您还不会吗？

查询指定排名的元素

仍然考虑使用线段树上遍历实现。

如果遍历到 \(i\) 节点的子树中排名为 \(k\) 的数，我们只需要判断这个数在左子树或右子树即可（除非 \(l=r\)，否则不可能是该节点本身）。

考虑节点的 \(v\) （和）的意义。\(i\) 节点的 \(v\) 是原序列位于 \([l,r]\) 的个数。而左子节点的 \(v\) 是原序列位于 \([l,\lfloor\frac{l+r}{2}\rfloor]\) 的个数。右子节点的 \(v\) 是原序列位于 \([\lfloor\frac{l+r}{2}\rfloor+1,r]\) 的个数。

我们可以发现，如果 \(k\leq\) 左子节点的 \(v\)，那么它一定在左子树。否则在右子树（\(k\gt\) 左子节点的 \(v\)，说明左子节点容不下排名为 \(k\) 的树）。

于是我们可以写出代码：

int kth(int k,int &i,int l,int r){
    if(l==r) return l;
    if(t[ls].v>=k) return kth(k,ls,l,mid);
    else return kth(k-t[ls].v,rs,mid+1,r);
}

查询前驱 / 后继

前驱可以通过查询原来的数的排名前 \(1\) 位对应的数实现。后继可以通过查询比原来的数大 \(1\) 的数的排名对应得数实现。

// 前驱
(kth(rnk(1,x+MOV-1,root,1,MOV<<1),root,1,MOV<<1)-MOV)
// 后继
(kth(rnk(1,x+MOV,root,1,MOV<<1)+1,root,1,MOV<<1)-MOV)

P3369 【模板】普通平衡树

您需要写一种数据结构（可参考题目标题），来维护一些数，有 \(n\) 个操作，需要提供以下操作：

1. 插入 \(x\) 数
2. 删除 \(x\) 数(若有多个相同的数，应只删除一个)
3. 查询 \(x\) 数的排名(排名定义为比当前数小的数的个数 \(+1\) )
4. 查询排名为 \(x\) 的数
5. 求 \(x\) 的前驱(前驱定义为小于 \(x\)，且最大的数)
6. 求 \(x\) 的后继(后继定义为大于 \(x\)，且最小的数)

\(1\le n \le 10^5\)，\(|x| \le 10^7\)

普通平衡树模板题，可以使用权值线段树实现（在权值树状数组科技出现之前，权值线段树是最快的，也许比红黑树还快）

完整代码

权值线段树的其他应用

求值位于某个区间的元素个数

其实就是权值线段树的区间和。

求值位于某个区间的元素和

插入 \(i\) 时从单点加 \(1\) 改为单点加 \(i\)，删除类似。

然后转化为求权值线段树的区间和。

同理我们还可以求有没有值位于某一个区间的元素。

CF69E Subsegments

给出两个整数 \(n,k\) 和一个序列 \(a\)。

你需要对于每一个长度为 \(k\) 的区间。求出区间中仅出现过一次的元素的最大值。如果不存在仅出现过一次的元素，输出 Nothing。

\(1 \leq n \leq 10^5,1 \leq k \leq n,-10^9\leq a_i\leq 10^9\)

考虑使用权值线段树解决这个问题。

先将 \([1,k-1]\) 的元素插进权值线段树，然后对于每一个区间，维护一个类似滑动窗口的东西。我们滑动区间时删除不在窗口里的元素，插入新来的元素。然后考虑如何求出仅出现过一次的元素的最大值。

单点修改时，维护 \(t,v\)。\(t\) 表示元素个数，\(v\) 表示对答案的贡献。到达叶子节点时，先更新 \(t\)。如果 \(t=1\)，则 \(v=l\)，否则 \(v=0\)。然后 pushup 时对 \(v\) 取 \(\max\) 即可。答案为 Nothing 当且仅当根节点的 \(v=0\)。

至于值域问题，我们加上偏移值 \(10^9\)，然后使用动态开点线段树。

可持久化权值线段树

概述

可持久化权值线段树，又叫主席树。指的是权值线段树的可持久化版本。最经典的应用就是实现静态区间第 \(k\) 小。

一般的线段树单点修改，我们会遍历待修改的叶子节点到根节点的链，然后逐级修改。这样子非常省事，但是不利于版本之间的存储（没修改一次就要重新建一棵线段树，时间空间都无法接受）。

我们考虑每一次修改访问的链，拉出来成为一个新的链（记得完善树结构），在新的链上修改，这样只需要版本每一个版本的树根即可。如下图：

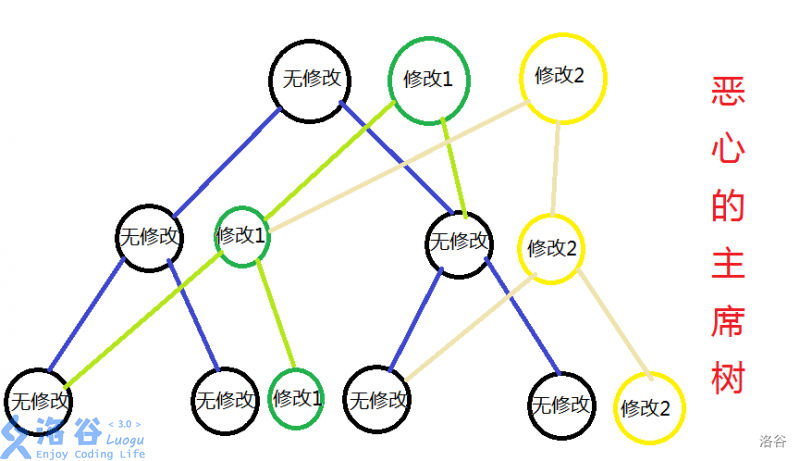
图片来源：P3919 【模板】可持久化数组 -初步探究主席树 - hyfhaha 的博客

这就是主席树。

P3834 【模板】可持久化线段树 2

这是个非常经典的可持久化权值线段树入门题——静态区间第 \(k\) 小。

给定 \(n\) 个整数构成的序列 \(a\)，有 \(m\) 个询问，每个询问对于指定的闭区间 \([l, r]\) 查询其区间内的第 \(k\) 小值。

\(1 \leq n,m \leq 2\times 10^5\)，\(|a_i| \leq 10^9\)，\(1 \leq l \leq r \leq n\)，\(1 \leq k \leq r - l + 1\)。

我们可以对于每一个 \(i\)，将 \(i\) 作为一个版本，将 \(a_i\) 插入到主席树中。

这样如果查询 \([l,r]\) 的第 \(k\) 小，关键之处在于左节点的 \(v\)，如果我们要查询版本区间的 \(v\) 和，我们可以考虑维护版本的前缀和即可。例子：如果我们需要到 \([l,r]\) 的某一个节点左节点的 \(v\)，只需要求出 \([1,r]\) 的减去 \([1,l-1]\) 的即可。（事实上主席树的最大应用就是维护差分信息）

至于前缀和如何维护，我们每一次插入的时候以前一个版本为基础即可。

时间复杂度 \(O((n+m)\log n)\)，空间复杂度 \(O(n\log n)\)。

说了这么多，下面我带大家写一下代码：

修改，修改单个节点，会自动重新创建一条链，并记录到 \(i\) 中：

inline void newnode(int &i){
    t[++tot]=t[i];i=tot;// 从 i 复制一个节点过来
}
void update(int p,int v,int &i,int l,int r){
    newnode(i); // 每到的节点都需要重新创建出来
    t[i].v+=v;
    if(l==r) return;
    if(p<=mid) update(p,v,ls,l,mid);
    else update(p,v,rs,mid+1,r);
}

查询，查询 \([\operatorname{ql},\operatorname{qr}]\) 的第 \(k\) 小。

注意实际上前缀和得 \(l\) 需要减去 \(1\)，但是在里面减一不方便，我们移到主函数里去减去 \(1\)。至于左子树右子树之类的我在上面讲过了。

int query(int ql,int qr,int k,int l,int r){
    if(l==r) return l;
    int delta=t[t[qr].l].v-t[t[ql].l].v; // 查询左子树元素个数
    if(delta>=k) return query(t[ql].l,t[qr].l,k,l,mid); // 在左子树
    else return query(t[ql].r,t[qr].r,k-delta,mid+1,r); // 在右子树
}

主程序：

int n,m,a[N],b[N];

signed main(){
    cin>>n>>m;
    for(int i=1;i<=n;i++) cin>>a[i];
	// 以下为初始化部分
    for(int i=1;i<=n;i++) b[i]=a[i];
    sort(b+1,b+n+1);
    int top=unique(b+1,b+n+1)-b-1; // 离散化三部曲：复制、排序、去重
    for(int i=1;i<=n;i++){
        int p=root[i-1];// 保存 i-1 版本树根
        update(lower_bound(b+1,b+top+1,a[i])-b,1,root[i-1],1,top); // 建出第 i 个版本，根暂存在 root[i-1] 中
        root[i]=root[i-1],root[i-1]=p; // 保存 root[i]，还原 root[i-1]
    }
	// 以上为初始化部分
    while(m--){
        int l,r,k;
        cin>>l>>r>>k;
        cout<<b[query(root[l-1],root[r],k,1,top)]<<'\n'; // 记得这里 l 要减去 1
    }
    return 0;
}

完整代码

P3567 [POI2014]KUR-Couriers

给出一个长度为 \(n\) 的正整数序列 \(a\)。共有 \(m\) 组询问，每次询问一个区间 \([l,r]\) ，是否存在一个数在 \([l,r]\) 中出现的次数严格大于一半。如果存在，输出这个数，否则输出 \(0\)。

\(1 \leq n,m \leq 5 \times 10^5\)，\(1 \leq a_i \leq n\)。

考虑修改查询函数。如果左子树的元素个数大于区间长度的一半，那么我们称左子树有希望，我们可以递归找找满不满足条件。如果右子树的元素个数大于区间长度的一半，我们称右子树有希望，我们可以递归找找满不满足条件。

如果到了叶子节点，说明 \(l\) 就是答案，返回。

如果没有子树有希望，我们返回 \(0\)。

不难发现，这样可以不重不漏地找到出现次数严格大于一半的数。

查询函数代码：

int query(int ql,int qr,int v,int l,int r){// v:区间长度
    if(l==r) return l;
    int lsiz=t[t[qr].l].v-t[t[ql].l].v,rsiz=t[t[qr].r].v-t[t[ql].r].v;
    if((lsiz<<1)>v) return query(t[ql].l,t[qr].l,v,l,mid);
    if((rsiz<<1)>v) return query(t[ql].r,t[qr].r,v,mid+1,r);
    return 0;
}

完整代码

P1972 [SDOI2009] HH的项链

给出一个长为 \(n\) 的序列 \(a\)，有 \(m\) 个询问，每个询问给出一个区间 \([l,r]\)，求出区间中有多少个不同的数字。

\(1 \leq n,m,a_i \leq 10^6\)

时间限制 \(2.00\text{s}\)，空间限制 \(512.00\text{MB}\)。

这是一道离线 + 树状数组练习题（莫队被 cz 卡得很惨）。不过也可以使用在线的主席树做。

做这道题时，我感觉 update 返回根节点比传引用好用，于是我把 update 改成了这样：

int update(int p,int v,int i,int l,int r){
    newnode(i);
    t[i].v+=v;
    if(l==r) return i;
    if(p<=mid) ls=update(p,v,ls,l,mid);
    else rs=update(p,v,rs,mid+1,r);
    return i;
}

我们设 \(L(i)\) 为 \(i\) 前面一个与 \(a_i\) 相同的数的下标（如果不存在，为 \(0\)）。

我们对于每一个时刻，对 \(L\) 建一棵权值线段树。也就是建可持久化权值线段树。

查询时我们发现 \([l,r]\) 内权值线段树的值都是重复的，我们统计一下位于这个区间的权值线段树中元素个数，用区间长度减去它即可。

注意这道题时空都非常紧张。所以不要 #define int long long！

完整代码

P4587 [FJOI2016]神秘数

一个可重复数字集合 \(S\) 的神秘数定义为最小的不能被 \(S\) 的子集的和表示的正整数。

现给定长度为 \(n\) 的正整数序列 \(a\)，\(m\) 次询问，每次询问包含两个参数 \(l,r\)，你需要求出由 \(a_l,a_{l+1},\cdots,a_r\) 所组成的可重集合的神秘数。

\(1\le n,m\le {10}^5\)，\(\sum a\le {10}^9\)

我们考虑每一个询问，设当前可以表示出来的区间为 \([1,x]\)。那么答案可能时 \(x+1\)，如果当前区间小于等于 \(x\) 的数的和 \(r\)（这个可以用权值线段树维护）大于等于 \(x+1\)，那么 \(x+1\) 不是最终的答案（因为可以被表示出来）,令 \(x=r+1\)，重复以上操作。如果小于，那么无法表示，答案就是 \(x\)。

可以证明，这个算法的时间复杂度为 \(O(n\log\sum a+m\log n\log\sum a)\)。可以通过本题。

完整代码

P3293 [SCOI2016]美味

有一个长为 \(n\) 的序列 \(a\)，有 \(m\) 个询问，每个询问给出两个整数 \(b,x\) 和一个区间 \([l,r]\)。求：

\[\max_{i=l}^{r}{(b \otimes (a_i+x))} \]

其中 \(a\otimes b\) 指 \(a\) 按位异或 \(b\)。

\(1 \le n \le 2 \times 10^5\)，\(0 \le a_i,b,x < 10^5\)，\(1 \le l \le r \le n\)，\(1 \le m \le 10^5\)

这道题最自然的思路是可持久化 01-Trie，但是我不会处理 \(x\)。

但是我们可以引入 01-Trie 求最大异或对的经典思想——按位贪心（从高位开始，每一位选当前可以选的最大的，可以简单地证明这个策略全局最优）。

设选出来的 \(a_i+x\) 为 \(K\)。

如果 \(b\) 的第 \(i\) 位为 \(1\)，那么最好填 \(0\)（因为 \(1\otimes 0=1\)）。填 \(0\) 不用累加 \(K\)。因此我们考虑什么时候需要填 \(1\)，也就是没有第 \(i\) 位为 \(0\) 的数。容易发现前 \(i+1\) 位来自 \(K\)，第 \(i\) 位为 \(0\) 的数位于一个连续区间 \([K,K+2^i-1]\)。看看有没有元素即可。

同理，若 \(b\) 的第 \(i\) 位为 \(0\)，那么最好填 \(1\)。第 \(i\) 位为 \(1\) 的位于 \([K+2^i,K+2^{i+1}-1]\) 区间内。看看有没有元素即可。

以上的分析过程没有考虑偏移值 \(x\)，我们只需要将上述所有区间的左右界减去 \(x\) 即可。

时间复杂度 \(O(n\log n+m\log n\log \max a)\)。

树状数组套可持久化权值线段树

概述

树状数组套可持久化权值线段树，又称带修改主席树，由于主席树可以看成权值线段树的前缀和。如果我们需要维护动态前缀和，我们一般会选择树状数组（如果你不怕常数大，也可以使用线段树）。所以我们自然想到用树状数组来辅助维护可持久化权值线段树，即树套树，来支持带修改的主席树。

P2617 Dynamic Rankings

给定一个含有 \(n\) 个数的序列 \(a_1,a_2 \dots a_n\)，需要支持两种操作：

• Q l r k 表示查询下标在区间 \([l,r]\) 中的第 \(k\) 小的数
• C x y 表示将 \(a_x\) 改为 \(y\)

\(1\le n,m \le 10^5\)，\(1 \le l \le r \le n\)，\(1 \le k \le r-l+1\)，\(1\le x \le n\)，\(0 \le a_i,y \le 10^9\)

如果去掉 C 操作，我们可以使用主席树简单地完成，加上 C 操作后，我们考虑使用带修改主席树完成。

先是主席树的基本操作，放上去即可：

struct node{
    int v,l,r;
} t[N<<5];
int tot,root[N];

void update(int p,int v,int &i,int l,int r){
    if(!i) i=(++tot);
    t[i].v+=v;
    if(l==r) return;
    if(p<=mid) update(p,v,ls,l,mid);
    else update(p,v,rs,mid+1,r);
}

然后是树状数组部分：

inline int lowbit(int x){return x&(-x);}

void update(int p,int v){// 单点修改
    for(int i=p;i<=n;i+=lowbit(i)) update(a[p],-1,root[i],0,1e9);
    a[p]=v;
    for(int i=p;i<=n;i+=lowbit(i)) update(a[p],1,root[i],0,1e9);
}

讲一下 update 函数。首先我们需要将原来的 \(a_p\) 清除，然后加上新的 \(a_p\)。树状数组的每一个节点都存储一个主席树（的根），修改时在对应的主席树上操作即可。

然后是重头戏，查询。查询时我们考虑在主席树的查询第 \(k\) 小的基础上进行修改。我们不再是维护一个节点，而是一次性维护树状数组维护的前缀权值线段树的所有节点对应的主席树（有点绕口，建议大家多读几遍）。

首先先将树状数组维护的主席树拉出来：

int lr[N],rr[N],tl,tr;// 左边的，右边的，左边计数器，右边计数器

inline void split(int l,int r){// 将 l-1 和 r 的主席树拉出来
    l--,tl=0,tr=0;
    for(int i=l;i;i-=lowbit(i)) lr[++tl]=root[i];
    for(int i=r;i;i-=lowbit(i)) rr[++tr]=root[i];
}

然后 kth 函数就不难写了：

int kth(int k,int l,int r){
    if(l==r) return l;
    int siz=0;
    for(int i=1;i<=tl;i++) siz-=t[t[lr[i]].l].v; // 减去 l-1
    for(int i=1;i<=tr;i++) siz+=t[t[rr[i]].l].v; // 加上 r
    if(k<=siz){
        // 所有节点改成左节点
        for(int i=1;i<=tl;i++) lr[i]=t[lr[i]].l;
        for(int i=1;i<=tr;i++) rr[i]=t[rr[i]].l;
        return kth(k,l,mid);
    }
    else{
        // 所有节点改为右节点
        for(int i=1;i<=tl;i++) lr[i]=t[lr[i]].r;
        for(int i=1;i<=tr;i++) rr[i]=t[rr[i]].r;
        return kth(k-siz,mid+1,r);
    }
}

然后这道题就做完了。

时间复杂度 \(O(n\log^2 n+m\log^2 n)\)，空间复杂度 \(O(n\log^2 n)\)。

完整代码

P3380 【模板】二逼平衡树（树套树）

您需要写一种数据结构（可参考题目标题），来维护一个初始长度为 \(n\) 的有序数列，有 \(m\) 个操作，需要提供以下操作：

1. 查询 \(k\) 在区间内的排名

2. 查询区间内排名为 \(k\) 的值

3. 修改某一位值上的数值

4. 查询 \(k\) 在区间内的前驱（前驱定义为严格小于 \(x\)，且最大的数，若不存在输出 -2147483647）

5. 查询 \(k\) 在区间内的后继（后继定义为严格大于 \(x\)，且最小的数，若不存在输出 2147483647）

\(1\le n,m\le5\times 10^4\)，序列中的值在任何时刻 \(\in[0,10^8]\)。

首先序列中的值太大了，我们先离散化（动态开点应该会喜提 MLE+RE+TLE 大礼包）。

然后 2,3 操作我们已经会了。

1 操作我们同样需要维护前缀和，也是使用 kth 差不多的方法，先 split 出来，然后统一维护，代码如下：

int rnk(int v,int l=1,int r=btot){
    if(l==r) return 1;
    if(v<=mid){
        for(int i=1;i<=tl;i++) lr[i]=t[lr[i]].l;
        for(int i=1;i<=tr;i++) rr[i]=t[rr[i]].l;
        return rnk(v,l,mid);
    }
    else{
        int siz=0;
        for(int i=1;i<=tl;i++) siz-=t[t[lr[i]].l].v;
        for(int i=1;i<=tr;i++) siz+=t[t[rr[i]].l].v;
        // 以上先把左边的求出来
        for(int i=1;i<=tl;i++) lr[i]=t[lr[i]].r;
        for(int i=1;i<=tr;i++) rr[i]=t[rr[i]].r;
        return siz+rnk(v,mid+1,r);
    }
}

4 操作我们考虑查询 \(k\) 的排名 \(p\)，然后访问排名为 \(p-1\) 的数。这个操作不合法当且仅当 \(p=1\)。

5 操作我们考虑查询 \(k+1\) 的排名 \(p\)，然后访问排名为 \(p\) 的数 \(s\)。这个操作合法仅当 \(s\neq k\) 且 \(p\leq r-l+1\)。

然后这道题我们也做完了。

完整代码

标签：le,int,线段,leq,详解,权值,节点
From： https://www.cnblogs.com/zheyuanxie/p/wsgt.html