[LeetCode] 684. Redundant Connection

In this problem, a tree is an undirected graph that is connected and has no cycles.

You are given a graph that started as a tree with n nodes labeled from 1 to n, with one additional edge added. The added edge has two different vertices chosen from 1 to n, and was not an edge that already existed. The graph is represented as an array edges of length n where edges[i] = [ai, bi] indicates that there is an edge between nodes ai and bi in the graph.

Return an edge that can be removed so that the resulting graph is a tree of n nodes. If there are multiple answers, return the answer that occurs last in the input.

Example 1:

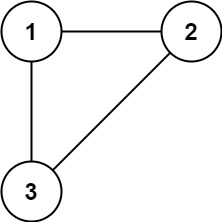
Input: edges = [[1,2],[1,3],[2,3]]
Output: [2,3]

Example 2:

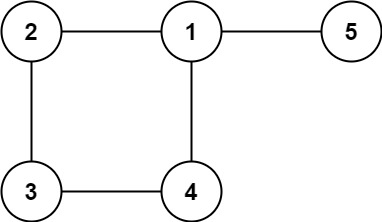
Input: edges = [[1,2],[2,3],[3,4],[1,4],[1,5]]
Output: [1,4]

Constraints:

• n == edges.length
• 3 <= n <= 1000
• edges[i].length == 2
• 1 <= ai < bi <= edges.length
• ai != bi
• There are no repeated edges.
• The given graph is connected.

冗余连接。

树可以看成是一个连通且 无环 的 无向 图。

给定往一棵 n 个节点 (节点值 1～n) 的树中添加一条边后的图。添加的边的两个顶点包含在 1 到 n 中间，且这条附加的边不属于树中已存在的边。图的信息记录于长度为 n 的二维数组 edges ，edges[i] = [ai, bi] 表示图中在 ai 和 bi 之间存在一条边。

请找出一条可以删去的边，删除后可使得剩余部分是一个有着 n 个节点的树。如果有多个答案，则返回数组 edges 中最后出现的边。

来源：力扣（LeetCode）
链接：https://leetcode.cn/problems/redundant-connection
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

思路是并查集。这是一道典型的并查集的题目。题目说给了一棵树但是多一条边，注意如果是树的话，如果节点数为 n 的话，那么边的数量是 n - 1。

我们用并查集的模板代码去遍历每条边，每条边都有两个端点 node，我们用并查集的方法去找每个 node 的父节点并记录下来。当我们遍历到某条边，发现这条边上的两个 node 的父节点是一样的时候，就说明这条边是多余的。

时间O(nlogn) - n个点，每个点找自己的父节点的复杂度 ≈ logn

空间O(n)

Java实现

 1 class Solution {
 2     public int[] findRedundantConnection(int[][] edges) {
 3         int[] parent = new int[2001];
 4         for (int i = 0; i < parent.length; i++) {
 5             parent[i] = i;
 6         }
 7         
 8         for (int[] e : edges) {
 9             int from = e[0];
10             int to = e[1];
11             if (find(from, parent) == find(to, parent)) {
12                 return e;
13             }
14             union(from, to, parent);
15         }
16         return new int[2];
17     }
18     
19     private int find(int node, int[] parent) {
20         while (node != parent[node]) {
21             node = parent[node];
22         }
23         return node;
24     }
25     
26     private void union(int a, int b, int[] parent) {
27         int aRoot = find(a, parent);
28         int bRoot = find(b, parent);
29         if (aRoot == bRoot) {
30             return;
31         }
32         parent[aRoot] = bRoot;
33     }
34 }

LeetCode 题目总结