标签：直线 right mathbf 优秀论文 SLAM mathcal based array left

论文简介

提出了一种UV-SLAM的算法，整体建立与VINS-MONO的基础上：

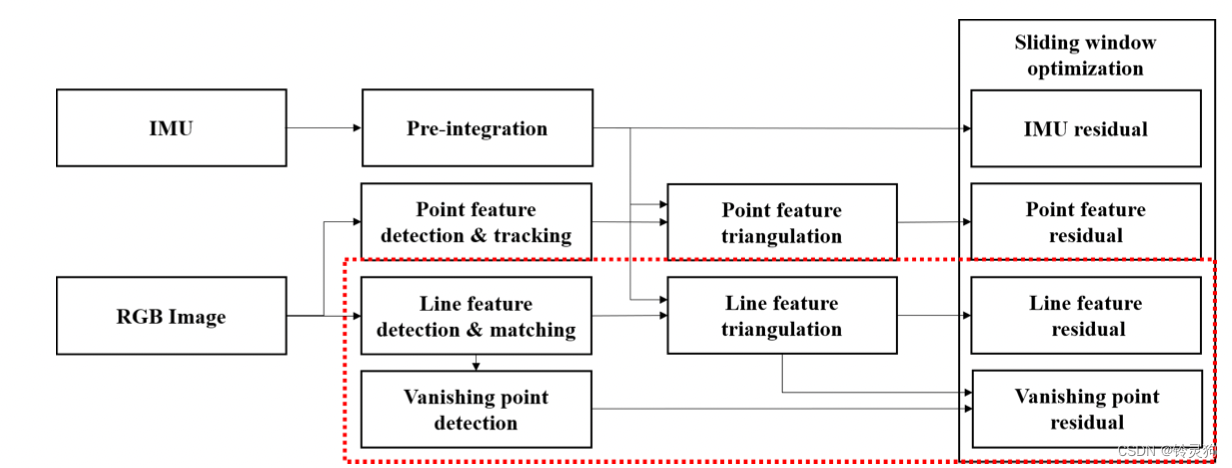
在VINS—MONO的基础上增加了线特征的约束和消影点的约束。
其中线特征的提取用的是line segment detector（LSD）算法，线特征的跟踪或线特征的描述子的提取用的是line binary descriptor（LBD）算法。
构建如下的误差方程：

\[\begin{array}{c} \min _{\mathcal{X}}\left\{\left\|\mathbf{r}_{0}-\mathbf{J}_{0} \mathcal{X}\right\|^{2}\right. \\ +\sum_{i \in \mathcal{B}}\left\|\mathbf{r}_{I}\left(\mathbf{z}_{b_{i+1}}^{b_{i}}, \mathcal{X}\right)\right\|_{\Sigma_{b_{i+1}}^{b_{i}}}^{2}+\sum_{(i, j) \in \mathcal{P}} \rho_{p}\left\|\mathbf{r}_{p}\left(\mathbf{z}_{p_{j}}^{c_{i}}, \mathcal{X}\right)\right\|_{\Sigma_{p_{j}}^{c_{i}}}^{2} \\ \left.+\sum_{(i, k) \in \mathcal{L}} \rho_{l}\left\|\mathbf{r}_{l}\left(\mathbf{z}_{l_{k}}^{c_{i}}, \mathcal{X}\right)\right\|_{\Sigma_{l_{k}}^{c_{i}}}^{2}+\sum_{(i, k) \in \mathcal{V}} \rho_{v}\left\|\mathbf{r}_{v}\left(\mathbf{z}_{v_{k}}^{c_{i}}, \mathcal{X}\right)\right\|_{\Sigma_{v_{k}}^{c_{i}}}^{2}\right\} \end{array} \]

其中第一项为边缘化 后面分别对应IMU、point、line和vanishing point（消影点）

图构建如下：

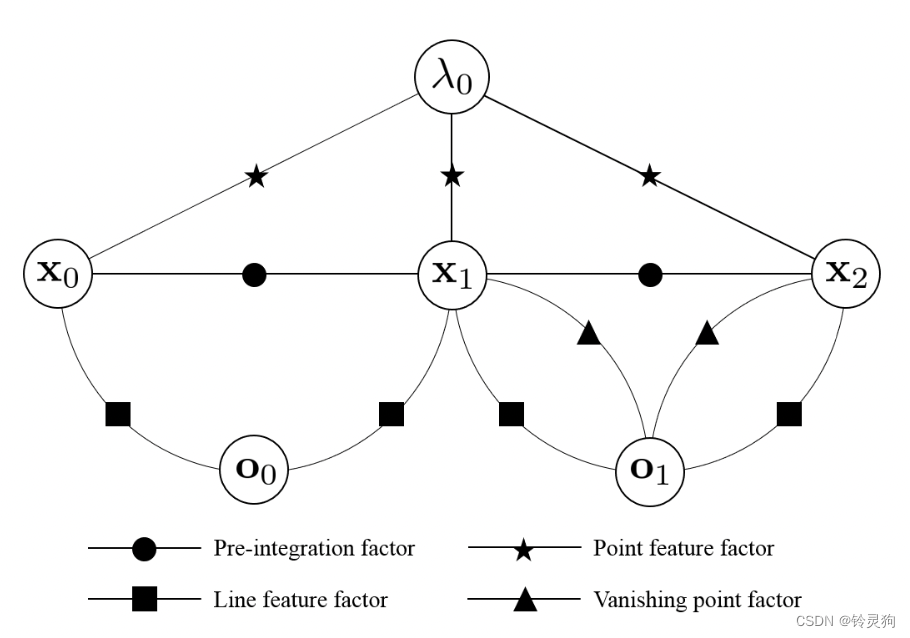
x为不同状态 原来只有预积分和特征点的边 现增加了线特征的边和消影点的边。
下面围绕着新增加的这两个边的约束进行讲解

线特征模型

两种直线表示法的说明：

原文中的讲解有一点点啰嗦 其实就是很正常的线特征误差函数构建。使用Plücker坐标系表示直线会用六个参数表示四自由度的直线 所以导致了六个参数并不是无约束的 因此这无法使用无约束优化 但是它的优点是初始化直线和空间变换的时候的形式表达非常简单。

因此在进行优化的时候 我们使用另一种直线的表达方式——正交表达。正交表达正好是四个参数表达四个自由度。且能够很方便的和Plücker坐标进行相互转换。

感性上构建直线残差的方式

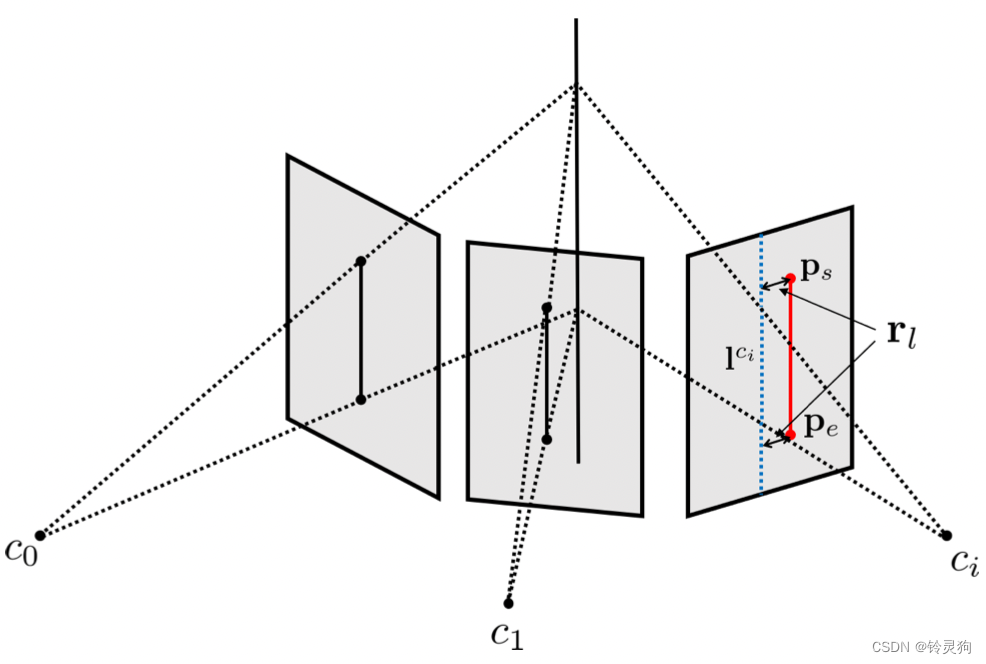
图片的说明如下：

清晰明了。图片为线特征残差构建的举例说明。直线通过另外两帧三角化得到再重投影到第三帧图像上，和第三帧图像上的对直线的观测求差构建目标函数。

这里有一个三维直线的投影说明。论文中的公式较为冗余，这里做简化说明：

\[l=\mathcal{K} \mathbf{n}=\left[\begin{array}{ccc} f_{y} & 0 & 0 \\ 0 & f_{x} & 0 \\ -f_{y} c_{x} & -f_{x} c_{y} & f_{x} f_{y} \end{array}\right] \mathbf{n} \]

\(l\)为重投影的直线表达形式 \(k\)为相机矩阵的内参 \(n\)为三维直线的Plücker坐标表示中的法向量 即直线和相机光心组成的平面的法向量

论文中强调 都是在归一化平面做处理 所以\(k\)为单位阵 导致二者直接相等了。

残差的构建 其实就是观测到的线段的端点分别到重投影直线的距离

\[\mathbf{r}_{l}=\left[\begin{array}{l} d\left(\mathbf{p}_{s}, \mathbf{l}^{c}\right) \\ d\left(\mathbf{p}_{e}, \mathbf{l}^{c}\right) \end{array}\right] \]

对状态量和直线的位置同时求雅可比进行优化。

消影点特征模型

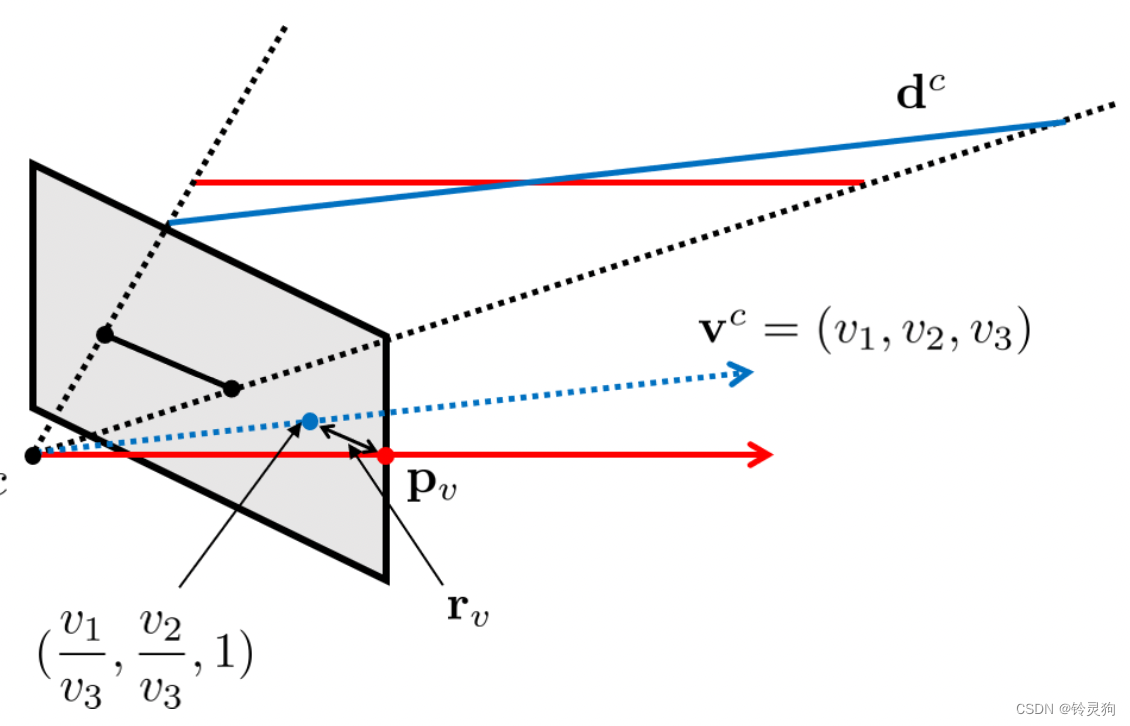
图中红色为观测的消影点 蓝色为计算的消影点。

计算消影点的方法：

\[\mathbf{v}^{c}=\left[\begin{array}{l}v_{1} \\v_{2} \\v_{3}\end{array}\right]=\lim _{t \rightarrow \infty} \mathbf{P}\left(\mathbf{V}_{0}+t \mathbf{D}\right)=\mathbf{K d}^{c}=\mathbf{d}^{c} \]

可以得到消影点的齐次坐标等于三维直线的方向向量

于是构建约束：

\[\mathbf{r}_{v}=\mathbf{p}_{v}-\frac{1}{v_{3}}\left[\begin{array}{l} v_{1} \\ v_{2} \end{array}\right] \]

关于雅可比的构建同线特征模型 这里不再赘述。

实验结果

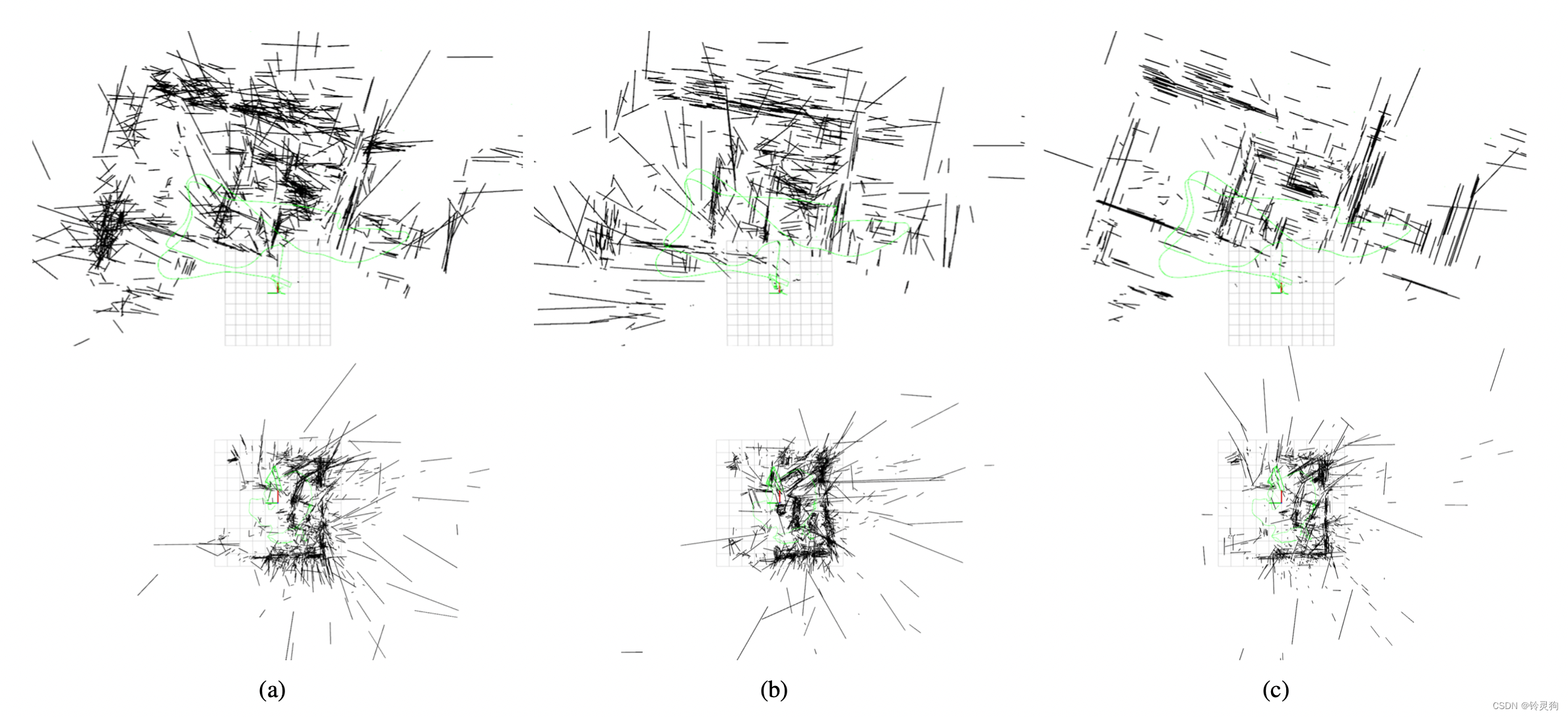
a为ALVIO的结果 b为该实验室以前的结果 c为本实验做出的结果

本文最大的亮点还是将消影点考虑进了残差内 得到的线特征比规整了很多。数据上看：

In addition, we showed that localization accuracy and mapping quality have increased through quantitative and qualitative comparisons with state-of-the-art algorithms. For future work, we will implement mesh or pixel-wise mapping through sparse line mapping from the proposed algorithm.

精度和质量都有提高 下一步工作是从稀疏的线条中恢复地图。

标签：直线,right,mathbf,优秀论文,SLAM,mathcal,based,array,left
From： https://www.cnblogs.com/linglingdog/p/17059851.html