题目描述
给定一棵树,树中包含 \(n\) 个结点(编号\(1\)~\(n\))和 \(n-1\) 条无向边,每条边都有一个权值。
请你在树中找到一个点,使得该点到树中其他结点的最远距离最近。
解题思路
\(\qquad\)在一棵树上,每一个节点都有两种选择,向父亲走或者向儿子走。
\(\qquad\)所以我们不妨进行一下分类讨论:
\(\qquad\qquad\)定义 \(ans[x]\) 为经过 \(x\) 点的最长路径,则可以分成两部分
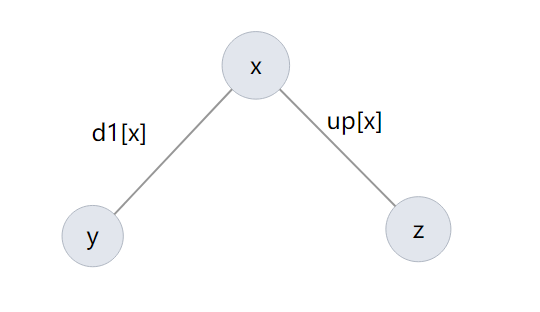
如图所示,从 \(x\) 出发向子节点走的最大距离 \(d1[x]\) 和从 \(x\) 出发向父节点走的最大距离 \(up[x]\),则 \(ans[x] = d1[x] + up[x]\)
但是可能会出现特殊情况,如下图所示:
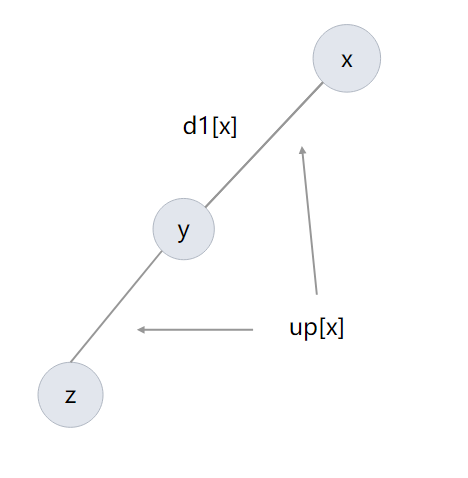
这时候我们不能这样走了,因为重边不划算,所以我们可以维护一个次大值,当发现这种情况的时候我们就用次大值 \(d2[x]\) 加上 \(up[x]\) 来更新,如图所示
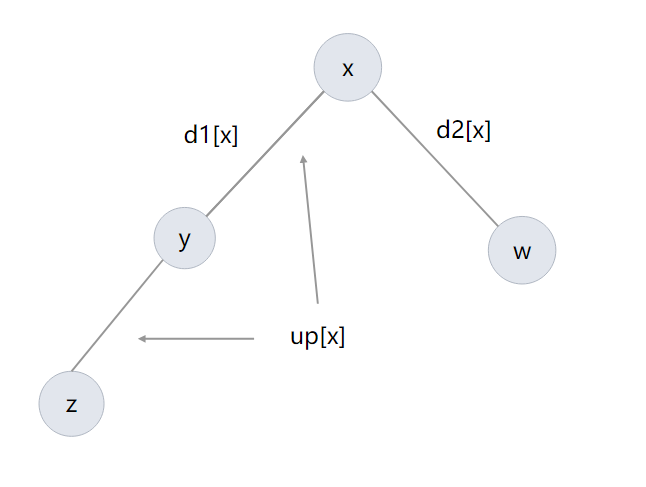
为什么次大值就不会出现重边呢,这里我们采用反证法:
我们先假设最大值和次大值经过同一个点,我们可以分析一下这段代码
int GoDown(int u, int fa)
{
for (int i = h[u]; ~i; i = ne[i])
{
int j = e[i];
if (j == fa) continue ; //遍历到父节点了
int dist = GoDown(j, u) + w[i]; // 递归子节点
//在这里的d1和d2一定是上一个子节点更新的,所以与dist找出来的子节点一定是不同的
if (dist >= d1[u]) //当d1被dist更新的时候,最长路的点是当前的点j
//而次长路被之前的最长路更新过了,所以这种情况最长路和次长路在不同子节点
{
d2[u] = d1[u], d1[u] = dist;
pre[u] = j;
}
else if (dist > d2[u]) d2[u] = dist;
//这种情况下,次长路被新节点更新,新节点与最长路所在的节点不同
//因此不管是哪种情况都一定能保证最长路与次长路不经过同一子节点
//注意只是子节点,后面的路径不能保证
}
if (d1[u] == 0) leaf[u] = true ; //没被更新就是叶子,因为所有边的权重都大于0
return d1[u];
}
证明完成,接下来可以直接上代码了
代码
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 2e5 + 10, INF = 0x3f3f3f3f;
int h[N], e[N], ne[N], w[N], idx;
int d1[N], d2[N], up[N]; //d1存一个数向子节点走的最大距离,d2次大,up是向父节点走的最长距离
int leaf[N], pre[N], n; //
void add(int a, int b, int c) // 添加一条边a->b,边权为c
{
e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx ++ ;
}
int GoDown(int u, int fa)
{
for (int i = h[u]; ~i; i = ne[i])
{
int j = e[i];
if (j == fa) continue ; //遍历到父节点了
int dist = GoDown(j, u) + w[i]; // 递归子节点
if (dist >= d1[u])
{
d2[u] = d1[u], d1[u] = dist;
pre[u] = j;
}
else if (dist > d2[u]) d2[u] = dist;
}
if (d1[u] == 0) leaf[u] = true ; //没被更新就是叶子,因为所有边的权重都大于0
return d1[u];
}
void GoUp(int u, int fa)
{
for (int i = h[u]; ~i; i = ne[i])
{
int j = e[i];
if (j == fa) continue ;
if (pre[u] == j) up[j] = max(d2[u], up[u]) + w[i];
else up[j] = max(d1[u], up[u]) + w[i];
GoUp(j, u);
}
}
int main()
{
scanf("%d", &n);
memset(h, -1, sizeof h);
for (int i = 1; i < n; i ++ ) //读入树
{
int u, v, w;
scanf("%d%d%d", &u, &v, &w);
add(u, v, w), add(v, u, w);
}
GoDown(1, -1), GoUp(1, -1); //以1为根节点进行DP
int res = d1[1];
for (int i = 2; i <= n; i ++ )
{
if (leaf[i]) res = min(res, up[i]); // 叶子节点不能向子节点走
else res = min(res, max(up[i], d1[i])); // 否则就向两个方向走
}
printf("%d\n", res);
return 0;
}