前置芝士
团
设 \(V\) 为 \(G\) 子图,当 \(V\) 中任意两点都有边相连,则 \(V\) 为 \(G\) 的一个团。
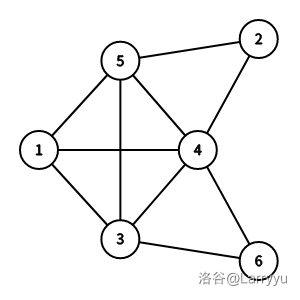
此图为本题样例
最大团: \(\{1,3,4,5\}\)
大小为 \(\dfrac {1}{3}n\) 的团: \(\{1,3\}\space \{3,6\} \space \{ 1,5\} \space \{1,4\}\space \{3,5\} \space \{4,5\}\space\{3,4\}\space\{4,6\}\space \{4,2\}\space\{5,2\}\)
一点点的图论
Description
给定一个大小为 \(n\) 的图,保证 \(n\) 为 \(3\) 的倍数,且存在一个大小为 \(\dfrac {2}{3}n\) 的团,要求输出一个大小为 \(\dfrac {1}{3}n\) 的团(输出点编号即可)。
Solution
由题意得: 至少有 \(\dfrac {2}{3}n\) 个点两两相连,所以剩下的 \(\dfrac {1}{3}n\) 个点与这个大小为 \(\dfrac {2}{3}n\) 两两不一定相连。那就只要见一对点不相连,就删一对,见两对删两对。明显,最多只会删 \(\dfrac {1}{3}n\) 对点,也就是 \(\dfrac {2}{3}n\) 个点,剩下的点即为题目所求。
结合样例
\(\{1,2\}\) 无连边,删去。
\(\{5,6\}\) 无连边,删去。
\(\{3,4\}\) 即为题目所求 。
Code
int n,m,cnt;
bool is_con[10010][10010],vis[10010]; //是否连边或删除
int main(){
cin>>n>>m;
for(int i=1;i<=m;i++){
int a,b;
cin>>a>>b;
is_con[a][b]=is_con[b][a]=1; //连边
}
for(int i=1;i<=n;i++){
if(vis[i]) continue;
for(int j=1;j<=n;j++){
if(j==i||vis[j]||is_con[i][j]) continue; //已经删了或不
vis[i]=1; //满足删的条件
vis[j]=1;
break;
}
}
for(int i=1;i<=n;i++){
if(vis[i]) continue;
cout<<i<<" ";
cnt++;
if(cnt==n/3) return 0; //大小已满足
}
cout<<endl;
return 0;
}