前置知识
三角函数。
引文
给定一个中心点 \(O\) 与 \(n\) 个点,求按点与 \(O\) 的连线与 \(x\) 轴的夹角排序后的点对。
正文
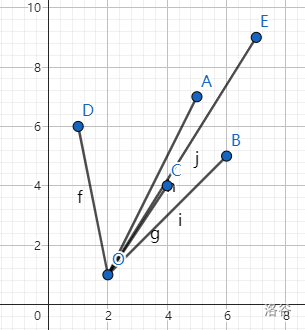
显而易见,不论我们如何移动 \(O\) 点,
点对都是不变的,所以,化难为简,索性将 \(O\) 点直接移动到原点上,
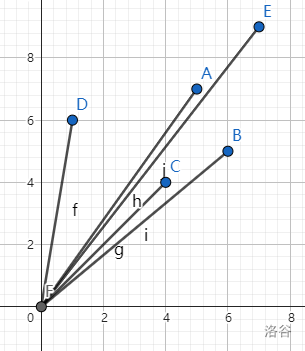
然后同过三角函数,我们可以算出这个角度,
直接调用 \(tan\) 的反函数 \(atan\) (备注: \(atan\) 或许精度更加准确),求出角度,
然后根据角度进行排序。
代码
struct point { // 存储点
double x,y;
};
double cross(double x1,double y1,double x2,double y2){ // 计算叉积
return (x1 * y2 - x2 * y1);
}
double compare(point a,point b,point c){ // 计算极角
return cross((b.x - a.x), (b.y - a.y), (c.x - a.x), (c.y - a.y));
}
bool cmp1(point a,point b) {
if (atan2(a.y, a.x) != atan2(b.y, b.x)) {
return atan2(a.y, a.x) < atan2(b.y, b.x);
}
else return a.x<b.x;
}