题目链接。
WC2023 之前补一下 WC2022 的题,参考了官方题解。
首先,把括号序列转化为二叉树,\(\texttt{(A)B}\) 转为一个点的左子树是 \(A\),右子树是 \(B\)。相当于括号序列先转为森林,再通过左儿子右兄弟转化为二叉树。
前四种操作对应的树上操作:
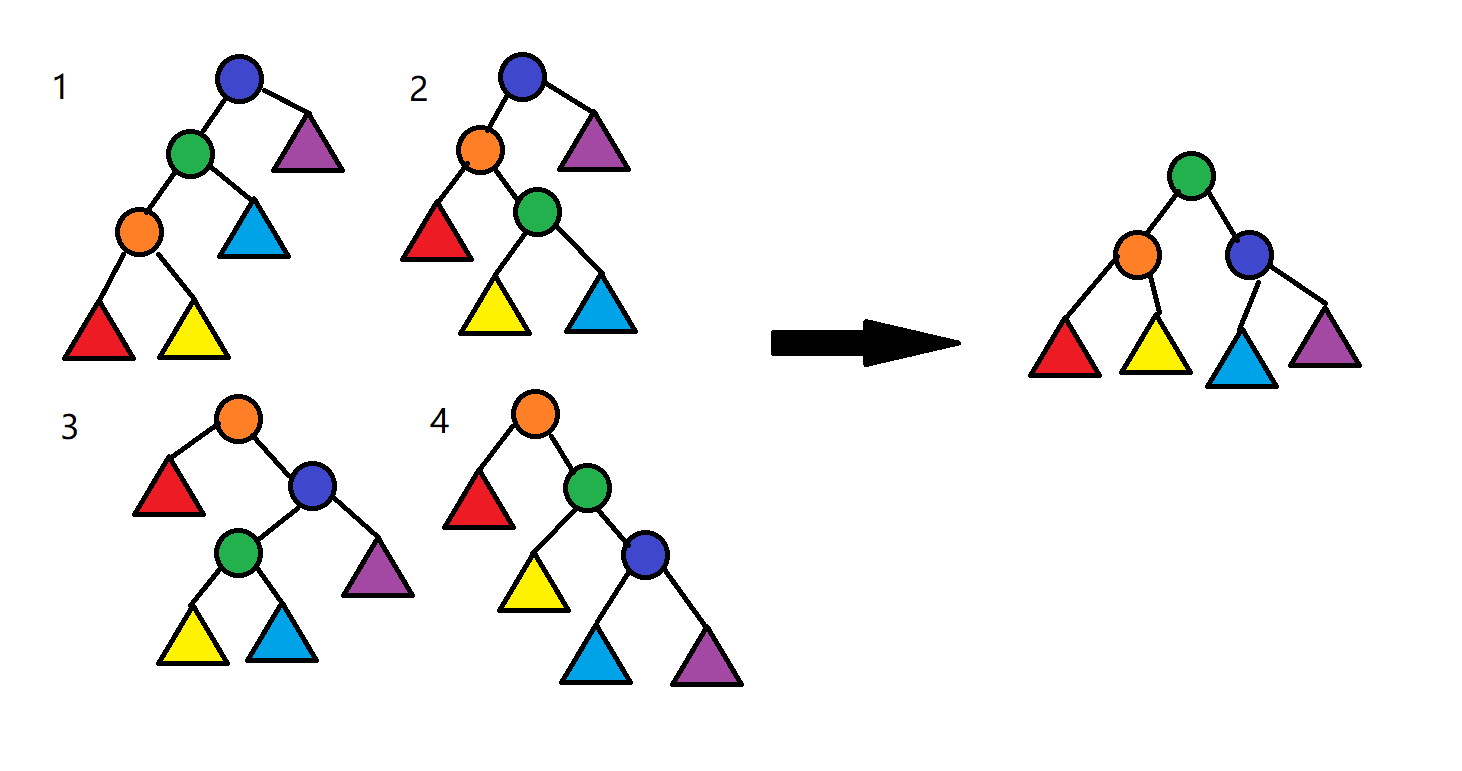
操作 1、4 类似于平衡树的旋转。这四种操作都不会改变二叉树的中序遍历。
操作 5、6 相当于添加、删除一个没有左儿子的点。
考虑先把 \(s_1\) 变换为 \(\texttt{(())()()()()}\) 的形式,即对应的二叉树只有根节点有左儿子。
从二叉树右链的底端开始操作。
- 若无左儿子,说明当前子树已经是右链,考虑父节点。
- 若左儿子有左儿子,对当前点使用操作 1,此时右链长度增加 \(1\)。
- 若左儿子只有右儿子,对当前点使用操作 2,此时右链长度增加 \(1\)。
- 若左儿子为叶子节点且当前点不是根,对父节点使用操作 3,右链长度不变,而此时上图黄、蓝子树为空,故当前点(对应上图深蓝色节点)不再有左儿子。
操作 1、2 会使右链长度增加 \(1\),右链长度最多从 \(1\) 增加到 \(n - 1\),故操作 1、2 总次数不超过 \(n - 2\) 次。
操作 3 不会改变右链长度,对于右链上非根的点,最多作为深蓝色点操作 \(1\) 次,而右链有 \(n - 1\) 个点,故操作 3 次数不超过 \(n - 2\) 次。
最后删除根节点的左儿子,并在右链底端增加一个叶子节点。
然后把 \(s_2\) 用相反的操作变换为右链。从根开始,若存在左儿子,则对当前点反向使用操作 4;若不存在左儿子,则考虑右子树。
但如果直接这样做,当右链底存在左儿子时,无法反向使用操作 4,所以先在右链底端加一个节点,保证反向操作 4 总能进行。最后再删除这个点。
这时树上有 \(n + 1\) 个点,正向操作的初始状态右链长度为 \(n + 1\),每次操作 4 会使右链长度减少 \(1\),故操作 4 次数不超过 \(n\) 次。
总操作次数不超过 \(3n\),可以通过。
对于题目中要输出的 \(p\) 的长度,由于前四种操作的点都在右链上,操作点的子树对应括号序列的一段后缀,所以 \(p\) 的长度等于 \(2(m-size_x)\),\(m\) 为当前树上节点数,执行操作时需要维护子树大小。
参考代码(暂无数据,能通过样例,不保证正确性,欢迎 hack):
#include <bits/stdc++.h>
using namespace std;
const int N = 2e5 + 5;
int id, T, n, k, val[N];
char sa[N], sb[N];
int fa[N], ls[N], rs[N], siz[N], root;
inline void pushup(int x) {
siz[x] = siz[ls[x]] + siz[rs[x]] + 1;
}
void dfs(int x) {
if (ls[x]) dfs(ls[x]);
if (rs[x]) dfs(rs[x]);
pushup(x);
}
void build(char s[]) {
root = 0;
for (int i = 1; i <= n; ++i)
fa[i] = ls[i] = rs[i] = siz[i] = 0;
int cnt = 0;
stack<int> st;
for (int i = 1; i <= 2 * n; ++i) {
if (s[i] == '(') {
val[i] = ++cnt;
st.push(cnt);
if (i == 1) root = cnt;
else {
fa[cnt] = val[i - 1];
if (s[i - 1] == '(') ls[val[i - 1]] = cnt;
else rs[val[i - 1]] = cnt;
}
} else {
val[i] = st.top();
st.pop();
}
}
dfs(root);
}
inline void rotateA(int z) {
int y = ls[z], f = fa[z], c = rs[y];
rs[y] = z, fa[z] = y;
ls[z] = c, fa[c] = z;
rs[f] = y, fa[y] = f;
fa[0] = ls[0] = rs[0] = 0;
if (!f) root = y;
pushup(z);
pushup(y);
}
inline void rotateB(int z) {
int x = ls[z], y = rs[x], f = fa[z], b = ls[y], c = rs[y];
ls[y] = x, fa[x] = y;
rs[y] = z, fa[z] = y;
rs[x] = b, fa[b] = x;
ls[z] = c, fa[c] = z;
rs[f] = y, fa[y] = f;
fa[0] = ls[0] = rs[0] = 0;
if (!f) root = y;
pushup(x);
pushup(z);
pushup(y);
}
inline void rotateC(int x) {
int z = rs[x], y = ls[z], f = fa[x], b = ls[y], c = rs[y];
ls[y] = x, fa[x] = y;
rs[y] = z, fa[z] = y;
rs[x] = b, fa[b] = x;
ls[z] = c, fa[c] = z;
rs[f] = y, fa[y] = f;
fa[0] = ls[0] = rs[0] = 0;
if (!f) root = y;
pushup(x);
pushup(z);
pushup(y);
}
inline void rotateD(int y) {
int x = ls[y], f = fa[y], b = rs[x];
rs[x] = y, fa[y] = x;
ls[y] = b, fa[b] = y;
rs[f] = x, fa[x] = f;
fa[0] = ls[0] = rs[0] = 0;
if (!f) root = x;
pushup(y);
pushup(x);
}
typedef pair<int, int> pii;
vector<pii> ans1, ans2;
void work(int x) {
while (x) {
while (ls[x]) {
if (ls[ls[x]]) {
ans1.emplace_back(1, 2 * (n - siz[x]));
rotateA(x);
} else if (rs[ls[x]]) {
ans1.emplace_back(2, 2 * (n - siz[x]));
rotateB(x);
} else if (fa[x]) {
ans1.emplace_back(3, 2 * (n - siz[fa[x]]));
rotateC(fa[x]);
} else {
break;
}
}
x = fa[x];
}
}
void workB() {
int x = root;
while (x) {
if (ls[x]) {
ans2.emplace_back(4, 2 * (n + 1 - siz[x]));
rotateD(x);
x = fa[x];
} else {
x = rs[x];
}
}
}
inline void clear() {
for (int i = 1; i <= 2 * n; ++i)
val[i] = sa[i] = sb[i] = 0;
for (int i = 1; i <= n + 1; ++i)
fa[i] = ls[i] = rs[i] = siz[i] = 0;
root = 0;
ans1.clear();
ans2.clear();
}
void solve() {
cin >> n >> k >> (sa + 1) >> (sb + 1);
build(sa);
int R = root;
while (rs[R]) R = rs[R];
work(R);
if (ls[root]) {
ans1.emplace_back(6, 1);
ans1.emplace_back(5, 2 * n - 2);
}
ans1.emplace_back(5, 2 * n);
build(sb);
R = root;
while (rs[R]) R = rs[R];
rs[R] = n + 1;
fa[n + 1] = R;
dfs(root);
ans2.emplace_back(6, 2 * n);
workB();
reverse(ans2.begin(), ans2.end());
cout << ans1.size() + ans2.size() << '\n';
for (pii p : ans1) {
int x, y;
tie(x, y) = p;
cout << x << ' ' << y << '\n';
}
for (pii p : ans2) {
int x, y;
tie(x, y) = p;
cout << x << ' ' << y << '\n';
}
clear();
}
int main() {
ios::sync_with_stdio(0);
cin.tie(0);
cin >> id >> T;
while (T--) solve();
return 0;
}