二分图
定义
给出一张图(通常是无向图),如果存在一种方案让这个图满足以下性质:
- 将图中的点分为两个点集,分别为左点集和右点集。
- 没有任意一条边的端点来自同一个点集。
那么我们称这张图为二分图。
换一种说法,如果将图中的边理解为两人之间关系的话:
如果可以将一张图中的点分为男生和女生且不存在同性恋关系(SP3377 A Bug's Life),那么这张图为二分图。
比如说这就是一张二分图。
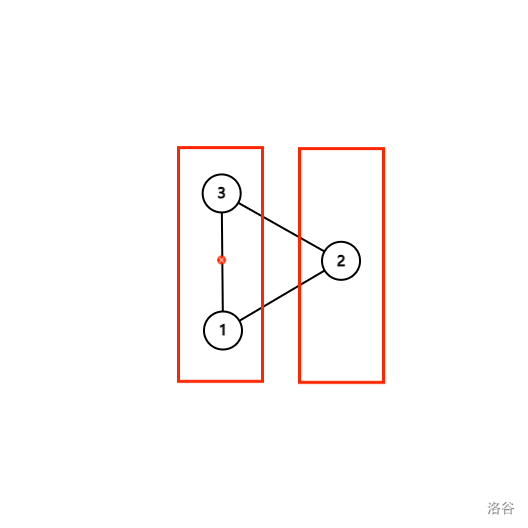
这不是二分图。
有一点需要记住,那就是 所有的树都是二分图。
判断
二分图的判断很简单,用 染色法 即可。根据二分图的定义,我们感性理解就可以得到如果这张图是二分图,那么相邻两点的颜色一定不同。
就拿上面这张图举例。

首先枚举第 1 个点:
- 给第 1 个点染白色(用 1 表示)。
- 发现第 1 个点连向第 2 个点以及第 3 个点,它们都没有染上色,所以给它们都染上黑色(用 2 表示)。
接着去看第 2 个点:
- 第 2 个点已经被染色,所以不用再继续染色。
- 发现第 2 个点连向第 1 个点以及第 3 个点,第 1 个点是白色,符合条件。但是第 2 个点连向了第 3 个点,第 2 个点和第 3 个点都是黑色,不满足二分图的条件,所以这张图不是二分图。
过程就是这么简单,接下来看代码。
我们以 洛谷P1330 封锁阳光大学 为例。
1 存图以及加边
这里我用的链式前向星存图。
如果不知道什么是链式前向星的话,可以左转看这里。
2 核心部分
比较好理解的代码,采用 DFS 完成二分图判断。
由于这道题需要我们求最小的河蟹数量,感性的理解就用两个变量 \(x\),\(y\) 记录左点集和右点集的点的数量,求出 \(x\) 和 \(y\) 的最小值就是答案。
还要注意这道题的图可能不是连通的,会产生多个二分图,需要多次判断。
DFS部分:
void dfs(int u,int c)//二分图染色+判断
{
color[u]=c;//染色
if(color[u]==1) x++;//记录点集1
if(color[u]==2) y++;//记录点集2
for(int i=head[u];i;i=e[i].nxt)//遍历以i为起点的每一条边
{
int j=e[i].to;//终点
if(color[j]>0)//如果j点已经染色
{
if(color[j]==c)//如果j点的颜色和起点颜色c相同,不满足二分图性质
f=1;
}
else dfs(j,3-c);//继续染色
}
}
3 完整代码
#include<bits/stdc++.h>
using namespace std;
int n,m,u,v,f,x,y,ans;
struct edge
{
int to,nxt;
} e[2*100005];
int head[100005],color[100005],cnt;
void init()//初始化函数
{
for(int i=0;i<=n;i++) head[i]=-1;
cnt=0;
}
void add(int u,int v)//链式前向星加边
{
e[++cnt].to=v;
e[cnt].nxt=head[u];
head[u]=cnt;
}
void dfs(int u,int c)//二分图染色+判断
{
color[u]=c;//染色
if(color[u]==1) x++;//记录点集1
if(color[u]==2) y++;//记录点集2
for(int i=head[u];i;i=e[i].nxt)//遍历以i为起点的每一条边
{
int j=e[i].to;//中点
if(color[j]>0)//如果j点已经染色
{
if(color[j]==c)//如果j点的颜色和起点颜色c相同,不满足二分图性质
f=1;
}
else dfs(j,3-c);//继续染色
}
}
int main()
{
init();
scanf("%d%d",&n,&m);
for(int i=1;i<=m;i++)
{
scanf("%d%d",&u,&v);
add(u,v);
add(v,u);
}
for(int i=1;i<=n;i++)
{
if(!color[i])//无向图不一定连通,需要多次搜索
{
x=y=0;
dfs(i,1);
if(f==0) ans+=min(x,y);
}
}
if(f==1) printf("Impossible\n");
else printf("%d\n",ans);
}
二分图最大匹配
1 定义
在二分图的边集中选出一个子集,使得子集中所有边的节点互不相交。
2 求二分图最大匹配
用 匈牙利算法 求解。匈牙利算法分为DFS版本和BFS版本,DFS较为好理解,BFS效率更高。
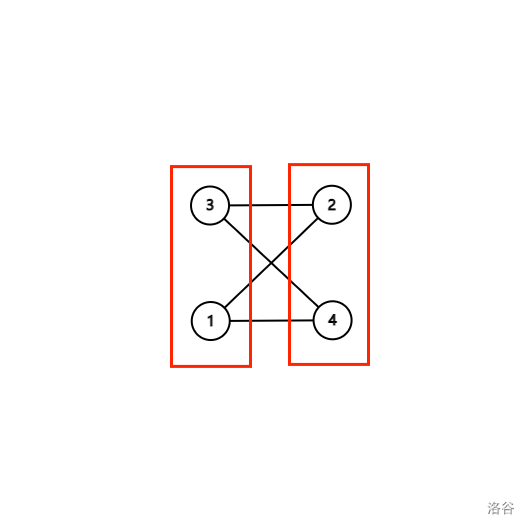
先介绍DFS基本实现过程。我们以这张图为例。

首先看 3 号点:
- 3 号点连向 2 号点以及 4 号点。因为 2 号点没有被访问过,且 2 号点没有与它匹配的点。所以我们记录 2 号点的匹配点是 3 号点。
接着看 1 号点:
- 1 号点连向 2 号点以及 4 号点。因为 2 号点没有被访问过,但是 2 号点已经有与它相匹配的 3 号点了。这时候该怎么办?
- 我们考虑给 2 号点当前匹配的点 ———— 3 号点换一个匹配的点,我们发现 3 号点还连向了 4 号点,所以我们将 3 号点与 4 号点相匹配。
- 这样就可以将 1 号点与 2 号点相匹配了。
所有的左部点都遍历了,循环结束,求出答案为 2。
3 完整代码
#include<bits/stdc++.h>
using namespace std;
int n,m,num,u,v,t,vis[5050],a[5050],ans;
//vis[i]表示 i 点是否被访问过。
//a[i]表示 i 点相连的左部点的编号。
//t表示时间标记,会用在vis[i]的判断中。如果觉得复杂,可以在每一轮搜索的时候memset一下,但是要注意时间复杂度。
struct edge
{
int to,nxt;
} e[100000];
int head[505],cnt;
void add(int u,int v)
{
e[++cnt].to=v;
e[cnt].nxt=head[u];
head[u]=cnt;
}
bool fnd(int x)
{
for(int i=head[x];i;i=e[i].nxt)
{
if(vis[e[i].to]==t) continue;//如果已经访问过了
vis[e[i].to]=t;//更新时间标记
if(!a[e[i].to]||fnd(a[e[i].to]))//如果e[i].to这个点还没有相匹配的点 或者 e[i].to这个点相匹配的点可以找到另一个右部点来匹配
{
a[e[i].to]=x;
return true;
}
}
return false;
}
int main()
{
scanf("%d%d%d",&n,&m,&num);
for(int i=1;i<=num;i++)
{
scanf("%d%d",&u,&v);
add(u,v);//注意这里加有向边
}
for(int i=1;i<=n;i++)
{
t=i;//记得更新时间标记
if(fnd(i)) ans++;
}
printf("%d\n",ans);
}
二分图最小点覆盖
1 定义
从二分图点集中选出一个子集,使得二分图中的边至少有一个端点在子集中。这样的子集中点数最少的就称为二分图最小点覆盖。
2 定理
二分图最小点覆盖=二分图最大匹配数。
二分图最大独立集
1 定义
从二分图点集中选出一个子集,使得子集中的点两两没有边相连。这样的子集中点数最多的就称为二分图最大独立集。
2 定理
二分图最大独立集=点总数-二分图最小点覆盖数。
二分图最大加权匹配
题单
洛谷:二分图
标签:二分,匹配,个点,int,color,号点 From: https://www.cnblogs.com/wangchai2009/p/17045572.html