关于置换环我们先从ABC241的E题引入
题面如下:
输入输出样例
输入 #1
5 3
2 1 6 3 1
输出 #1
11
输入 #2
10 1000000000000
260522 914575 436426 979445 648772 690081 933447 190629 703497 47202
输出 #2
826617499998784056
解:
这道题先给定一个n和一个k
再给出A数列,X表示盘子中现有的糖果数
往后执行k次操作,每次操作加入A[x%n]颗糖
咳咳,经过分析我们可以知道x%n最多只有n个取值,也就是说我们可以预先把这些值都处理出来
例如对于样例
2 1 6 3 1
产生的图为。
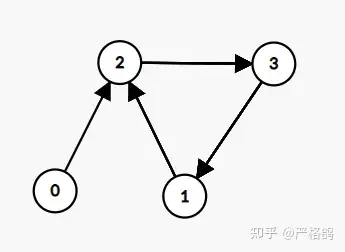
所有的操作会产生一条链和一个环,环里的操作都是循环往复的
链上的操作可以单独计算,对于k次操作,我们可以减去链的长度来判断在环上走了多远
核心代码:
const int N=2e5+10;
int n,m,k,a[N],b[N],p[N];
int pre[N],id[N];
void solve(){
//try it again.
cin>>n>>k;
up(0,n-1)cin>>a[o];
id[0]=0;
up(1,n-1)id[o]=-1;//预处理,id==-1的点就是没有被循环过的点
pre[0]=0;//起点
int st=0,ed=0;
up(0,n-1){
pre[o+1]=pre[o]+a[pre[o]%n];//o是操作的次数
if(id[pre[o+1]%n]!=-1){//已经循环过就成环了
st=id[pre[o+1]%n];//第一次前往这个点的点
ed=o+1;//这个点的次数
break;
}
id[pre[o+1]%n]=o+1;//经过这个点更新一次
}
int ans=0;
if(k<=st)ans=pre[k];//未进入循环节,计算链的值
else{
int len=ed-st;//一次循环所用的次数
int val=pre[ed]-pre[st];//一次循环所放进的糖果数
int x1=(k-st-1)/len;//经过的循环数
int x2=(k-st-1)%len;//未走完剩下的步数
ans=x1*val+pre[x2+st+1];//更新答案
}
puts(ans);//得到答案
}
经过刚才的这个题可以对环有一个新的认识
关于更详细的图论建议看严鸽鸽的这篇题解
Educational Codeforces Round 4 E(图论/构造) - 知乎 (zhihu.com)
//上面那个题有些难,可以去严鸽鸽的知乎看讲解
刚刚VP补了一道置换环的题
Codeforces Round #842 (Div. 2)
Problem - D - Lucky Permutation
题意大致是这样的:
给你一个数组,一次操作可以给数组的两个元素交换位置,请问需要多少次操作才能够让数组中仅存在一对逆序对
//PS:有一个小性质 一个数组中逆序对的数量就是将其还原到顺序所需的操作次数
//这个题也有一个特殊的性质,下面来讲一下(因为比较懒所以就直接引用严鸽鸽的了哈哈哈)
考虑置换环,也就是 i↔p[i] 之间连边。
例如以下排列 [1,7,5,8,2,6,3,4]
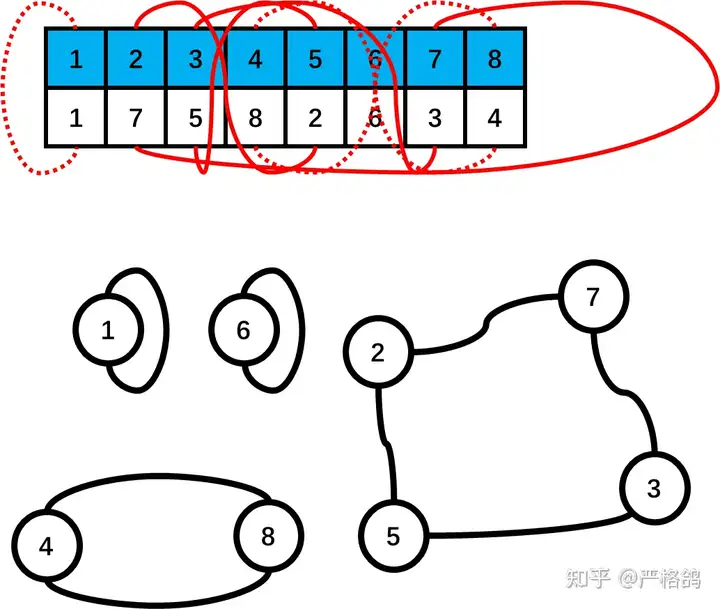
我们看看那个4个点的环
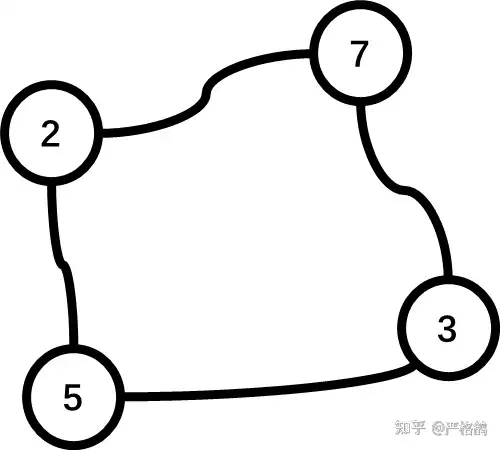
在排列上,进行交换
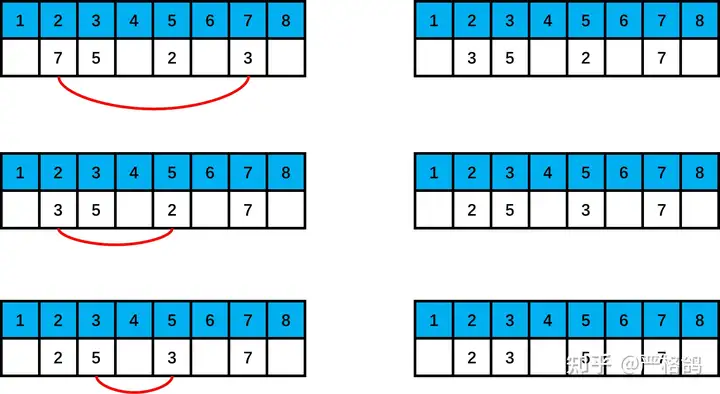
执行了3次交换,就可以使得4个数,到 [1,2,3,4,5...n] 相应的位置上。
如果有cur个环,那么只需要 n−cur 次交换就可以把排列变成 [1,2,3...n] 了。
然后执行一次相邻交换的操作就可以了。
但是,还有一种情况。
对于上面的4个点的环,我们这样交换
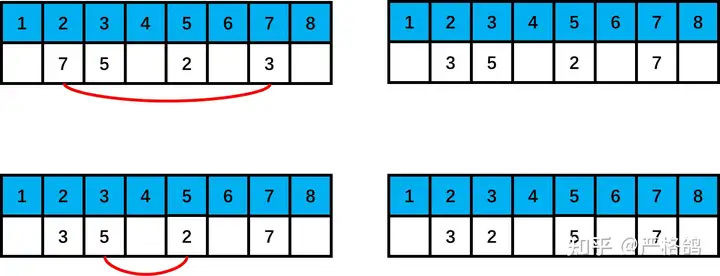
此时,我们交换了两次,而 p[2],p[3] 构成了一个逆序对。
也就是,如果环中,有相邻的两个点,那么可以通过减少一次交换,使得其贡献出一个逆序对。
此时的操作次数为 n−cur−1
//那么我们得到了一条很重要的性质
//如果一个数组中的任一置换环中有相邻的元素,那么将其还原到仅留一个逆序对所需的次数就是n-置换环的数量-1
//反之如果没有的话,那么所需的次数就是n-置换环的数量+1 (因为还原顺序以后就需要单独造出一对逆序对)
下面是这道题的主要代码
const int N=2e5+10;
int n,m,k,a[N],b[N],p[N];
bool vis[N];//计算所有的环
map<int,bool>mp;//计算每一个环
bool flag;
void dfs(int u){//搜环的数量
vis[u]=true;
mp[u]=true;
if(mp[u-1]||mp[u+1])flag=true;
if(!vis[a[u]])dfs(a[u]);
}
void solve(){
//try it again.
flag=false;
cin>>n;
up(1,n)vis[o]=false;
up(1,n)cin>>a[o];
int cnt=0;
up(1,n){
if(!vis[a[o]]){
cnt++;
mp.clear();
dfs(a[o]);
}
}
int gg=0;
if(flag)cout<<n-cnt-1<<endl;
else cout<<n-cnt+1<<endl;
}
