首页 > 其他分享 >MaoWei-2020-HistoryRepeatsItself-ECCV

MaoWei-2020-HistoryRepeatsItself-ECCV

时间：2023-01-06 21:44:14浏览次数：73  
标签：MaoWei tmp src kernel self 2020 dct HistoryRepeatsItself size

History Repeats Itself: Human Motion Prediction via Motion Attention #paper

1. paper-info

1.1 Metadata

  • Author:: [[Wei Mao]], [[Miaomiao Liu]], [[Mathieu Salzmann]]
  • 作者机构::
  • Keywords:: #DCT , #GCN , #Attention
  • Journal:: #ECCV
  • Date:: [[2020-07-22]]
  • 状态:: #Done
  • 链接:: http://arxiv.org/abs/2007.11755
  • 阅读时间:: 2023.01.05

1.2. Abstract

Human motion prediction aims to forecast future human poses given a past motion. Whether based on recurrent or feed-forward neural networks, existing methods fail to model the observation that human motion tends to repeat itself, even for complex sports actions and cooking activities. Here, we introduce an attention-based feed-forward network that explicitly leverages this observation. In particular, instead of modeling frame-wise attention via pose similarity, we propose to extract motion attention to capture the similarity between the current motion context and the historical motion sub-sequences. Aggregating the relevant past motions and processing the result with a graph convolutional network allows us to effectively exploit motion patterns from the long-term history to predict the future poses. Our experiments on Human3.6M, AMASS and 3DPW evidence the benefits of our approach for both periodical and non-periodical actions. Thanks to our attention model, it yields state-of-the-art results on all three datasets. Our code is available at https://github.com/wei-mao-2019/HisRepItself.

keywords:: GCN, DCT, Attention, HPM.

2. Introduction

  • 领域:: HMP -- Human motion prediction
  • 之前的方法::
    • Hidden Markov models
    • Gaussian Process Dynamical Models
    • RNN-based
  • 作者的方法主要针对RNN-based的方法
    • 问题::
      • RNN倾向于生成静态姿势，因为他们很难跟踪长期历史。
    • 方法::
      • attention-based motion prediction approach
      • Discrete Cosine Transform(DCT):: 利用运得到的动注意力作为权重，将整个DCT编码的运动历史聚合到历史的运动估计中。然后将该估计与最新观察的运动相结合，结果作为GCN的输入。(GCN 用于编码关节之间的空间依赖性。)
    • 方法动机:: 人体的动作序列总是重复的，(预测差异即可)

3. Methods

符号
\(X_{1:N}=[x_1,x_2,...,x_N]\):: 历史序列，时间长度为\(N\)。
\(x_i\in\mathbb{R}^K\)
\(X_{N+1:N+T}\):: 待预测序列。


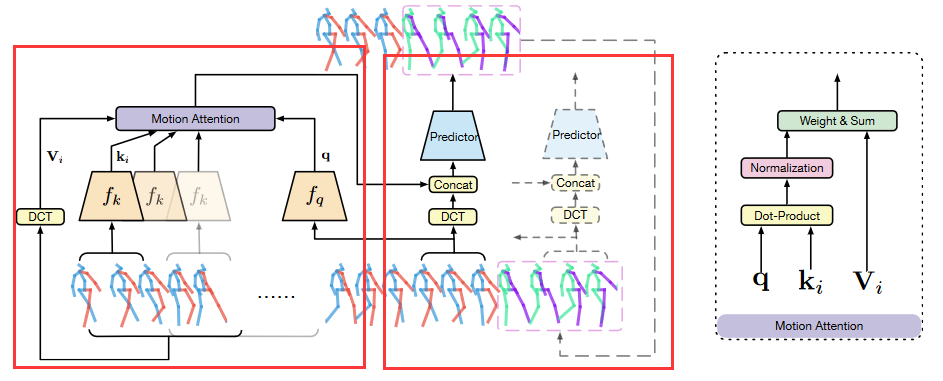
Fig.1.模型的结构。主要分为两部分，第一部分为Attention，计算注意力；第二部分为预测部分，预测器采用GCN。观测序列的最后M帧作为query，历史序列的前面部分中的M帧连续序列作为key,然后与DCT编码后的历史序列计算得到最后的注意力分数。将注意力分数作为权重与DCT编码的最后M帧串联作为Predictor的输入，然后通过自回归的方式进行预测。
Source: 源paper

3.1 Motion Attention Model

该注意力机制是基于动作序列大多重复的现象，也就是说该注意力机制是为了发现当先序列与历史序列之间的相似之处，该机制包含一个query，和多个key-value对。如图Fig.1的右边，最后计算的方式是通过Weight & Sum的方式，不同于传统的注意力机制。

将\(X_{1:N}\)分为多个\(\{X_{i:i+M+T-1}\}^{N-M-T+1}_{i=1}\)子序列

  • query:: last observed sub-sequence
  • key-value对::
    • key:: 历史子序列。\(X_{i:i+M-1}\)
    • value:: 历史子序列加上其对应的未来序列的DCT编码。\(X_{i:i+M+T-1}\)经过DCT编码后，会得到\(\{V_i\}_{i=1}^{N-M-T+1}\in \mathbb{R}^{K\times (M+T)}\) ,其中\(V_i\)的每一行对应了每一个关节点的DCT系数。
      注：由于后面的预测器采用的是GCN(作用于DCT编码)的方式，所以为了保持Attention model的输出与GCN的输入一致，这里的value为DCT编码。
      计算过程
      \(f_q:\mathbb{R}^{K\times M} \rightarrow \mathbb{R}^{d}\ and \ f_k:\mathbb{R}^{K\times M} \rightarrow \mathbb{R}^{d}\) :: 通过RELU的限制，让其中的值都非负，防止得到非负的注意力分数
      \(q = f_q(X_{N-M+1:N})\,\ k_i=f_k(X_{i:i+M-1})\)
      其中\(q,k_{i\in}\mathbb{R}^{d}\ and\ i\in \{1,2,...,N-M-T+1\}\)，对于每一个key，通过下面的公式计算注意力分数::

\[a_i=\frac{qk_i^T}{ {\textstyle \sum_{i=1}^{N-M-T+1}}qk_i^T } \]

不同于传统用softmax作为归一化的操作，这里使用的是sum。

然后结合\(V_i\)得到最后的输出::

\[U = \sum_{i=1}^{N-M-T+1}a_iV_{i} \; \in \mathbb{R}^{K\times (M+T)} \]

3.2 Prediction Model

GCN+DCT 的方式，DCT 用于捕捉时间信息，GCN用于捕捉空间信息。
DCT Temporal encoding
DCT \(\{C_{k,l}\}_{l=1}^{L}\)的计算方式::

\[C_{k,l}=\sqrt{\frac{2}{L} }\sum_{n=1}^{L}x_{k,n}\frac{1}{\sqrt{1+\delta_{l1} }} cos(\frac{\pi }{L}(n-\frac{1}{2} )(l-1) ) \]

IDCT的计算方式::

\[x_{k,n}=\sqrt{\frac{2}{L} }\sum_{l=1}^{L}x_{k,n}\frac{1}{\sqrt{1+\delta_{l1} }} cos(\frac{\pi }{L}(n-\frac{1}{2} )(l-1) ) \]

注：使用了同[1]的padding strategy，将\(M+T\)长度的DCT系数\(D\in \mathbb{R}^{K\times (M+T)}\)与注意力\(U\)作为输入。
GCN Spatial encoding
GCN 的公式::

\[H^{(p+1)} = \sigma(A^{(p)}H^{(p)}W^{(p)}) \; A^{(p)}\in \mathbb{R}^{K\times K} \; H^{(p)}\in \mathbb{R}^{K\times 2(M+T)} \; W^{(p)}\in \mathbb{R}^{F\times \hat{F}} \]

\(\; F = 2(M+T) \; 因为U+D的维度。\)

3.3 loss function

Mena Per Joint Position Error

4. Experiment

  • datasets
    • Human3.6M
    • AMASS
    • 3DPW
  • Evaluation Metrics
    • Mean Per Joint Position Error

5. 核心代码

class AttModel(Module):

    def __init__(self, in_features=48, kernel_size=5, d_model=512, num_stage=2, dct_n=10):
        """
        :params in_features: 输入的特征维度大小
        :params kernel_size: 对应论文中M的数量 过去帧数
        :params d_model: 注意力机制中的特征维度
        :params num_stage: 模型层数
        :params dct_n: DCT中保存程度数
        """
        super(AttModel, self).__init__()

        self.kernel_size = kernel_size
        self.d_model = d_model
        # self.seq_in = seq_in
        self.dct_n = dct_n
        # ks = int((kernel_size + 1) / 2)
        assert kernel_size == 10

        self.convQ = nn.Sequential(nn.Conv1d(in_channels=in_features, out_channels=d_model, kernel_size=6,
                                             bias=False),
                                   nn.ReLU(),
                                   nn.Conv1d(in_channels=d_model, out_channels=d_model, kernel_size=5,
                                             bias=False),
                                   nn.ReLU())

        self.convK = nn.Sequential(nn.Conv1d(in_channels=in_features, out_channels=d_model, kernel_size=6,
                                             bias=False),
                                   nn.ReLU(),
                                   nn.Conv1d(in_channels=d_model, out_channels=d_model, kernel_size=5,
                                             bias=False),
                                   nn.ReLU())

        # 用于预测的GCN
        self.gcn = GCN.GCN(input_feature=(dct_n) * 2, hidden_feature=d_model, p_dropout=0.3,
                           num_stage=num_stage,
                           node_n=in_features)

    def forward(self, src, output_n=25, input_n=50, itera=1):
        """

        :param src: [batch_size,seq_len,feat_dim]
        :param output_n: 输出序列长度
        :param input_n: 输入序列长度
        :param itera: 迭代次数
        :return:
        """
        dct_n = self.dct_n                                                                  # dct_n DCT中的保留程度
        src = src[:, :input_n]  # [bs,in_n,dim]                                             # src: 得到输入序列 历史序列
        src_tmp = src.clone()                                                               # str_tmp 用于后面的更新
        bs = src.shape[0]                                                                   # bs: batch_size 的大小
        src_key_tmp = src_tmp.transpose(1, 2)[:, :, :(input_n - output_n)].clone()          # src_key_tmp: 注意力中的key [bs,feature_dim, i->N-T+1]
        src_query_tmp = src_tmp.transpose(1, 2)[:, :, -self.kernel_size:].clone()           # src_query_tmp: 注意力中的query对应序列的最后一个子序列 [bs, feature_dim, -kernel-size]

        dct_m, idct_m = util.get_dct_matrix(self.kernel_size + output_n)                    # 得到DCT and IDCT 系数矩阵[M+L, M+L] kernel_size 对应论文中的M 
        dct_m = torch.from_numpy(dct_m).float().cuda()                                      # 将DCT 系数矩阵转为tensor and to GPU
        idct_m = torch.from_numpy(idct_m).float().cuda()                                    # 将IDCT 系数矩阵转为tensor and to GPU

        vn = input_n - self.kernel_size - output_n + 1                                      # vn: 除去最后一个子序列的历史序列，用于计算注意力 N-M-T+1
        vl = self.kernel_size + output_n                                                    # vl: M+L
        idx = np.expand_dims(np.arange(vl), axis=0) + \
              np.expand_dims(np.arange(vn), axis=1)                                         #
        src_value_tmp = src_tmp[:, idx].clone().reshape(
            [bs * vn, vl, -1])                                                              # src_value_tmp: 注意力机制中的value，
        src_value_tmp = torch.matmul(dct_m[:dct_n].unsqueeze(dim=0), src_value_tmp).reshape(
            [bs, vn, dct_n, -1]).transpose(2, 3).reshape(
            [bs, vn, -1])  # [32,40,66*11]                                                  # 计算DCT编码后的value值

        idx = list(range(-self.kernel_size, 0, 1)) + [-1] * output_n                        
        outputs = []

        key_tmp = self.convK(src_key_tmp / 1000.0)                                          # key_tmp: [batch_size, d_model] 论文中的f_k
        """自回归，迭代的预测"""
        for i in range(itera):
            query_tmp = self.convQ(src_query_tmp / 1000.0)                                  # query_tmp: [batch_size, d_model] 论文中的f_q
            score_tmp = torch.matmul(query_tmp.transpose(1, 2), key_tmp) + 1e-15            # 计算 当前子序列的注意力分数
            att_tmp = score_tmp / (torch.sum(score_tmp, dim=2, keepdim=True))               # 归一化 注意力分数
            dct_att_tmp = torch.matmul(att_tmp, src_value_tmp)[:, 0].reshape(
                [bs, -1, dct_n])                                                            # dct_att_tmp: 计算得到论文中的U

            input_gcn = src_tmp[:, idx]                                                     # 得到GCN的原始输入
            dct_in_tmp = torch.matmul(dct_m[:dct_n].unsqueeze(dim=0), input_gcn).transpose(1, 2) # DCT编码
            dct_in_tmp = torch.cat([dct_in_tmp, dct_att_tmp], dim=-1)                       # 论文中的U+D
            dct_out_tmp = self.gcn(dct_in_tmp)                                              # gcn 的预测输出
            out_gcn = torch.matmul(idct_m[:, :dct_n].unsqueeze(dim=0),      
                                   dct_out_tmp[:, :, :dct_n].transpose(1, 2))               # IDCT 得到最后的动作序列 
            outputs.append(out_gcn.unsqueeze(2))                                            # 将结果加入最终输出
            if itera > 1:
                # update key-value query
                out_tmp = out_gcn.clone()[:, 0 - output_n:]                                 # out_tmp 预测的一个序列
                src_tmp = torch.cat([src_tmp, out_tmp], dim=1)                              # src_tmp 将预测的加入src
                """更新 key-value query 然后计算方式同上"""
                vn = 1 - 2 * self.kernel_size - output_n                                    
                vl = self.kernel_size + output_n
                idx_dct = np.expand_dims(np.arange(vl), axis=0) + \
                          np.expand_dims(np.arange(vn, -self.kernel_size - output_n + 1), axis=1)

                src_key_tmp = src_tmp[:, idx_dct[0, :-1]].transpose(1, 2)
                key_new = self.convK(src_key_tmp / 1000.0)
                key_tmp = torch.cat([key_tmp, key_new], dim=2)

                src_dct_tmp = src_tmp[:, idx_dct].clone().reshape(
                    [bs * self.kernel_size, vl, -1])
                src_dct_tmp = torch.matmul(dct_m[:dct_n].unsqueeze(dim=0), src_dct_tmp).reshape(
                    [bs, self.kernel_size, dct_n, -1]).transpose(2, 3).reshape(
                    [bs, self.kernel_size, -1])
                src_value_tmp = torch.cat([src_value_tmp, src_dct_tmp], dim=1)

                src_query_tmp = src_tmp[:, -self.kernel_size:].transpose(1, 2)

        outputs = torch.cat(outputs, dim=2)
        return outputs

[1]Mao, W., Liu, M., Salzmann, M., Li, H.: Learning trajectory dependencies for human motion prediction. In: ICCV. pp. 9489–9497 (2019)

标签：MaoWei,tmp,src,kernel,self,2020,dct,HistoryRepeatsItself,size
From： https://www.cnblogs.com/guixu/p/17031663.html

相关文章

赞助商

阅读排行

网站主页关于我们联系我们网站地图

本网站内容转载自其他媒体，侵权联系[admin##ips99.com]。

Copyright © 2020-2023 IPS99 版权所有 IPS99