题解 校内考20230104 T2 旗木双翼

题目描述

菲菲和牛牛在一块 \(n\) 行 \(m\) 列的棋盘上下棋，菲菲执黑棋先手，牛牛执白棋后手。

棋局开始时，棋盘上没有任何棋子，两人轮流在格子上落子，直到填满棋盘时结束。落子的规则是：一个格子可以落子当且仅当这个格子内没有棋子且这个格子的左侧及上方的所有格子内都有棋子。

Itachi 听说有不少学弟在省选现场 AC了 D1T1，解决了菲菲和牛牛的问题，但是 Itachi 听说有的人认为复杂度玄学，Itachi 并不想难为学弟学妹，他想为大家节约时间做剩下的题，所以将简化版的 D1T1带给大家。

Itachi 也在一块 \(n\) 行 \(m\) 列的棋盘上下棋，不幸的是 Itachi 只有黑棋，不过幸好只有他一个人玩。现在，Itachi 想知道，一共有多少种可能的棋局（不考虑落子顺序，只考虑棋子位置）。

Itachi 也不会为难学弟学妹们去写高精度，所以只需要告诉 Itachi 答案 \(\bmod 998244353\)（一个质数）的结果。

思路

由于一个格子可以落子当且仅当这个格子内没有棋子且这个格子的左侧及上方的所有格子内都有棋子，则作为一种结果，其从上到下每行的棋子个数是不严格单调递减的，如下图：

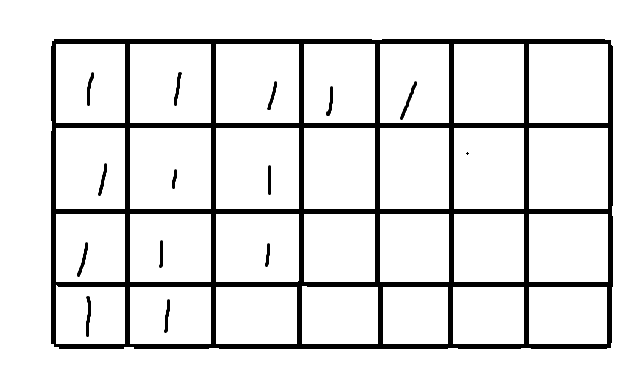
按行分析，只考虑每行的棋子个数，得到一个不严格单调递减序列，由于序列长度和范围固定，则考虑排列组合。但排列组合选的数各不相同，于是要想办法将其变成一个严格单调递减序列且不影响结果。

将最后一行加上 \(1\) 个棋子，倒数第二行加上 \(2\) 个棋子...第一行加上 \(n\) 个棋子，于是得到了下图：

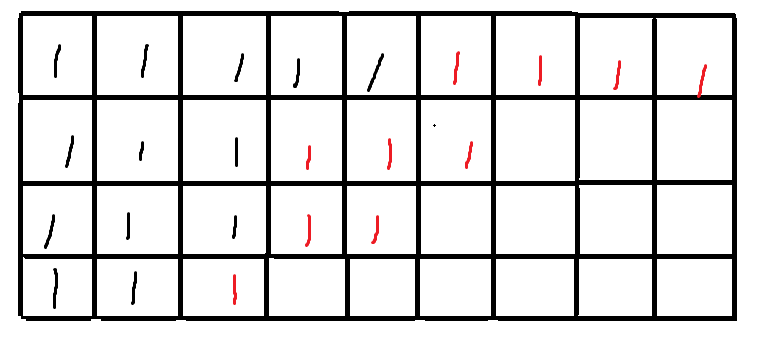
这样一来，原先的序列 \(5,3,3,2\) 变成了现在的序列 \(9,7,5,3\) 成了严格单调笛剑序列且与前面的序列一一对应，则达到了先前的目的，可以进行排列组合。 考虑到第一行最多可以有 \(n+m\) 列，最后一行最少可以有 \(1\) 列（原本可以没有，加上了一个棋子），则问题就转化成了在 \([1,n+m]\) 范围内，任选 \(n\) 个数（一共有 \(n\) 行），有多少种结果。很明显，答案就是 \(C_{n+m}^n\) 。最后，由于 \(n,m\) 较大，且题目在疯狂暗示 \(9982443353\) 是个质数，所以要求逆元。

CODE

#include <bits/stdc++.h>
typedef long long ll;
using namespace std;
template<typename T>inline T read(){
    T a=0;bool s=0;
    char ch=getchar();
    while(ch>'9' || ch<'0'){
        if(ch=='-')s^=1;
        ch=getchar();
    }
    while(ch>='0' && ch<='9'){
        a=(a<<3)+(a<<1)+(ch^48);
        ch=getchar();
    }
    return s?-a:a;
}
const int mn=1e5+10;
const int mod=998244353;
ll inv[mn];
inline void init(){
    inv[1]=1;
    for(int i=2;i<=100000;i++)
        inv[i]=(ll)(mod-mod/i)*inv[mod%i]%mod;
}
int main(){
    // freopen("giveyouacandy.in","r",stdin);
    // freopen("giveyouacandy.out","w",stdout);
    int n=read<int>(),m=read<int>();
    init();
    ll ans=1;
    for(int i=1;i<=n+m;i++)
        ans=ans*i%mod;
    for(int i=1;i<=m;i++)
        ans=ans*inv[i]%mod;
    for(int i=1;i<=n;i++)
        ans=ans*inv[i]%mod;
    printf("%lld\n",ans);
    // while(1)getchar();
    return 0;
}