红黑树起源以及插入解析

红黑树的起源

二分查找具有Ologn的时间复杂度，使用二分查找的基础是数据有序。很明显数组可以完成这一条件，但是数组也有缺点，扩容，增加，删除非常不方便。而链表则没有这些缺点，但是链表却不满足随机存取，无法使用二分查找。解决方法便是二叉搜索树，而二叉搜索树的缺点是极端情况下链化又成为了链表。那么可以考虑平衡树，平衡树具有数据分布均匀的特性，但是由于其平衡要求过于严格，进行插入删除会频繁的调整树结构。因此，改善平衡树的特点就出现了红黑树。红黑树具有自平衡（相对平衡，并非平衡树）和有序的特性，很好的完成检索的需求。

红黑树中红黑的含义

红黑是为了保证树的平衡而产生的两种节点的表示。理解红黑之前，先了解另一种树，2-3树。2-3树同样是二叉搜索树的变种，具有名称中的2，3代表两种节点。

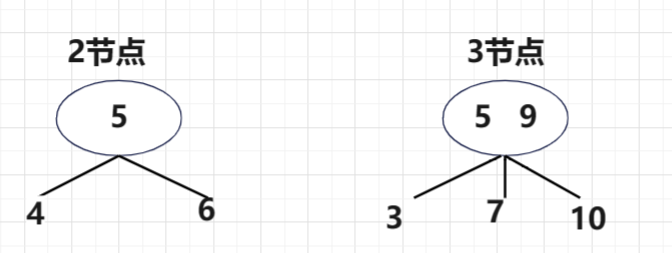
2节点：包含一个元素，两个子节点引用，左节点小于父节点，右节点大于父节点

3节点：包含两个元素，三个子节点引用，左边节点小于第一个父节点，中间节点大于第一个小于第二个父节点，右边节点大于第二个父亲节点。

检查2，3节点是否正确的一个有效方法是，节点全部投影到x轴此时为有序序列，如4，5，6和3，5，7，9，10。

两种节点搭配下，保证了任意叶子节点到根节点的距离相同，也就是数据分布均匀而不是链化。二叉搜索树链化的结果是因为插入操作，插入从根节点开始比较，大于走向右边，小于走向左边，走到空则进行插入。而2-3树插入正是改善了插入操作，从而完成相对平衡。

2节点插入一个元素，即成为3节点。

而3节点插入一个元素，需要分类讨论。

• 一、3节点没有父亲节点，即整棵树只有它一个三节点。那么三节点插入后将进行分解变成二叉搜索树

  

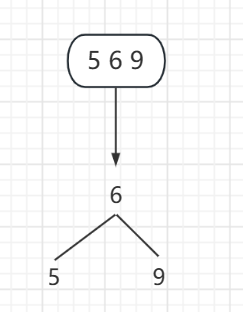
• 二、3节点有一个2节点的父亲节点。3节点插入分解后的得到的父节点融入到2节点成为3节点。

  

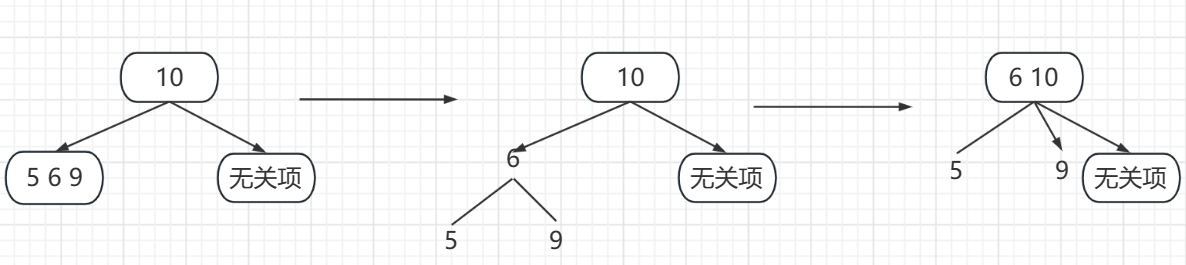
• 三、3节点的父亲节点为3节点。子3节点分解得到的父节点，融入到父3节点，父3节点再次分解

  

但是将这种思想直接转换为编码实现起来不是很方便，因为需要维护两种类型的节点还需要不断的分解和融合。因此，红黑树出现了，红黑树使用红色黑色的连接作为标记，区分2，3节点，使得代码思想实现更加凝练。

那么红色黑色是怎么标记的呢？在红黑树中，所有节点都是2节点，而3节点是通过连接两个2节点而表示的，连接一个黑色节点和一个红色节点。2-3树的所有叶子节点到树根的路径长度相同，在红黑树中转变为从所有叶子节点到树根的路径长度途径黑色节点的数目相同。因此红黑树并非平衡树，而是黑色节点平衡树。

使用图像表示

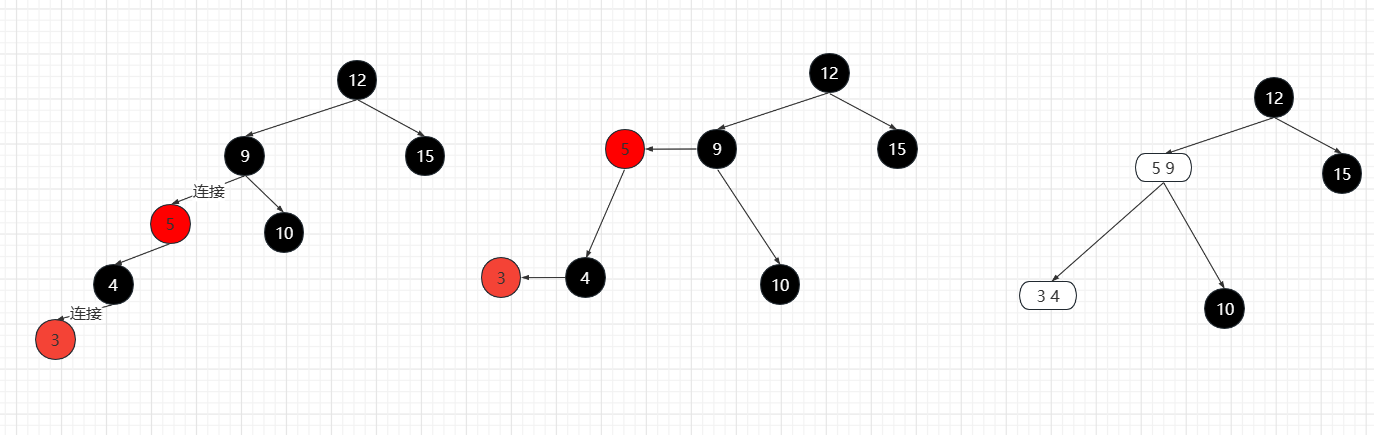
红黑树的性质

• 每个节点要么是红色，要么是黑色
• 根节点是黑色
• 每个叶子节点是黑色
• 两个红节点不直接相连，在2-3树相连会被分解
• 任意一节点到每个叶子节点的路径包含数量相同的黑节点

红黑树插入操作

插入操作为两步，第一是查找插入位置，第二则是插入后维护红黑树。

依靠三种操作维护红黑树：左旋、右旋、变色。左旋，右旋是为了保持平衡，变色时因为需要保持任意两个红色节点不直接相连。

• 变色：红黑转变

• 左旋：以某个节点作为旋转节点，其右子节点变为旋转节点的父亲节点，右子节点的左节点变为旋转节点的右子节点

  

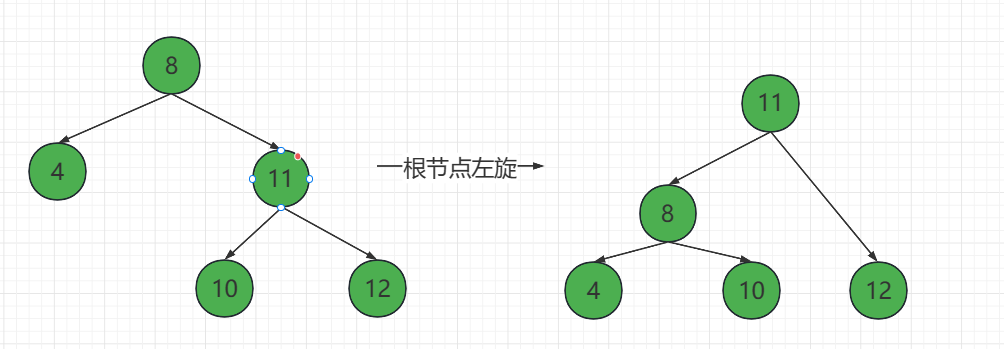
• 右旋：以某个节点作为旋转节点，其左子节点变为旋转节点的父亲节点，左子节点的右节点变为旋转节点的左子节点

  

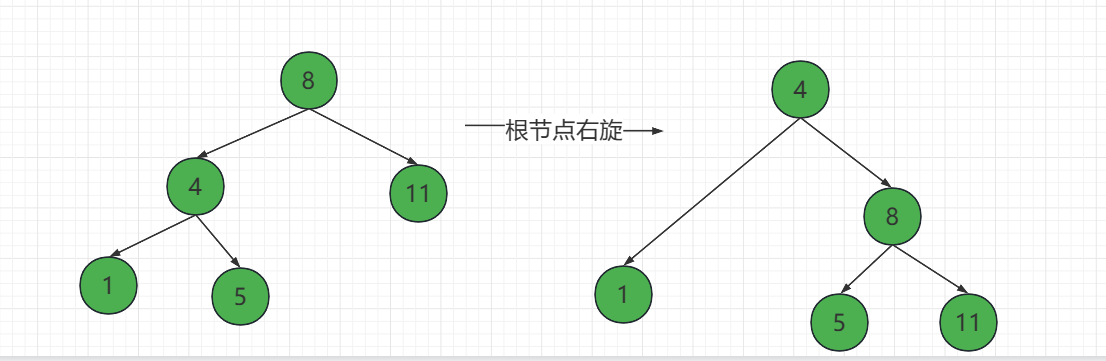
  注意：插入节点为红色节点。因为插入时需要保持黑色平衡，如果为黑色节点则有可能破坏，而红色节点一定不会破坏。

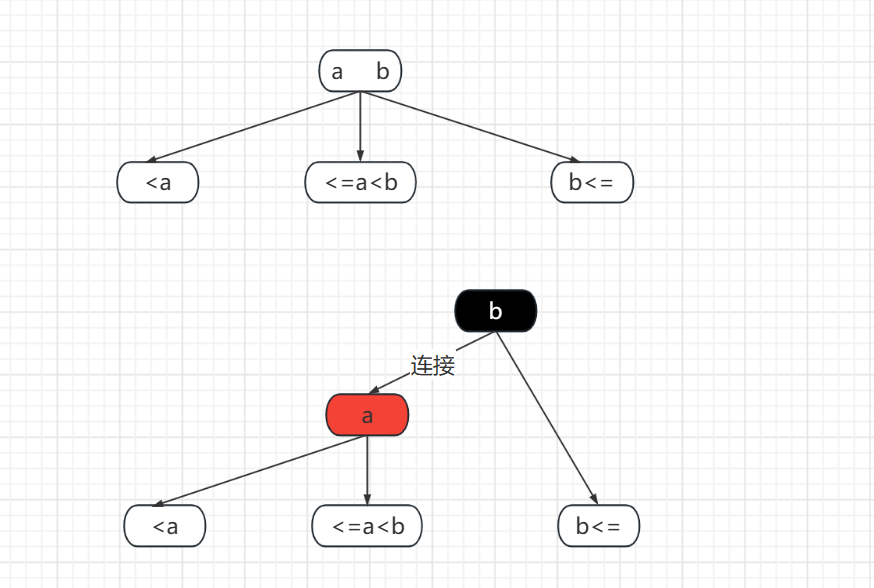
  我们约定如图

  

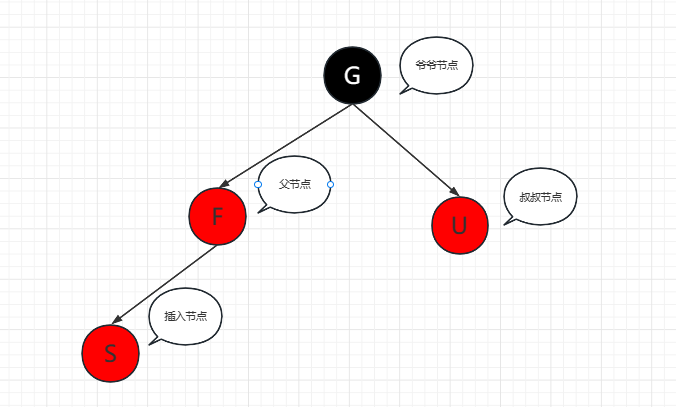
  插入环境分析

• 空树

  插入节点作为根节点，并且变为黑色

• 插入节点的key值已经存在

  更新节点值

• 插入节点的父节点为黑色节点

  直接插入即可

• 插入节点的父节点为红色节点

  因为一定还存在一个黑色根节点，因此此时一定存在爷爷节点。

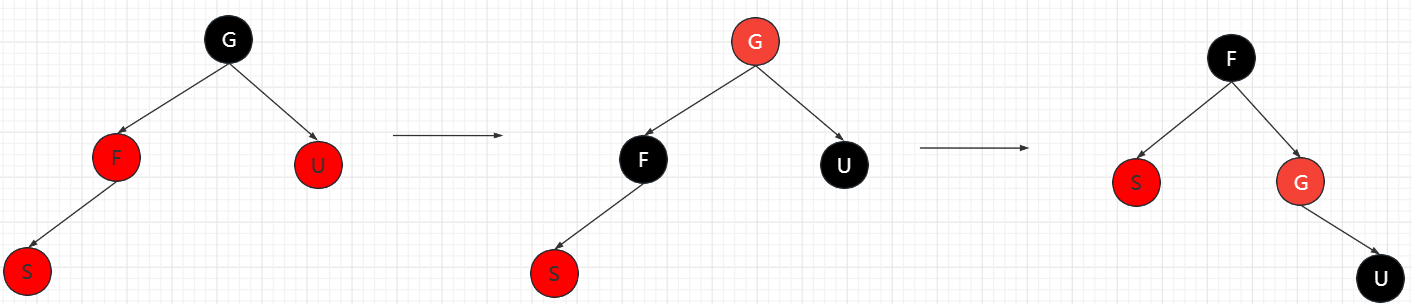
  • 叔叔节点存在并且为红色节点

    将F，U节点变为黑色，G变为红色，再设置G节点为当前插入节点。因为此时G节点此时就相当于一个插入节点

    

  • 叔叔节点不存在

    • 父节点为爷爷节点的左节点，

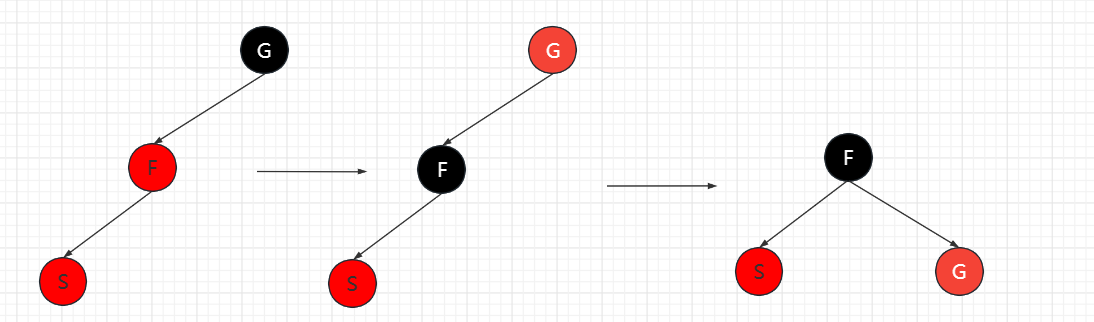
      • 插入节点为父节点的左节点（LL红）

        F节点变为黑色，G节点变为红色，对G节点进行右旋

      

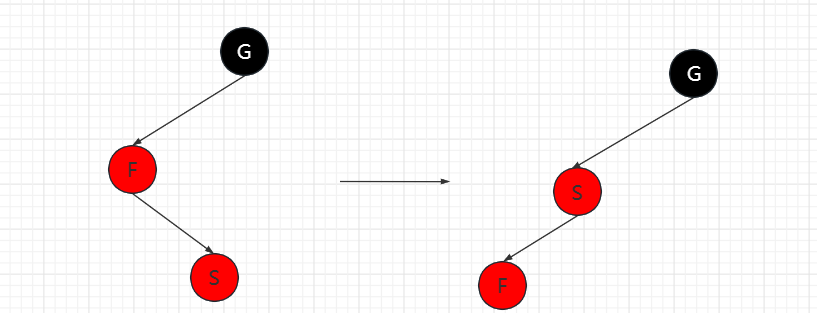
      • 插入节点为父节点的右节点（LR红）

        对F节点进行左旋，设置F节点为插入节点。此时便转换为LL红

        

    • 父节点为爷爷节点的右节点

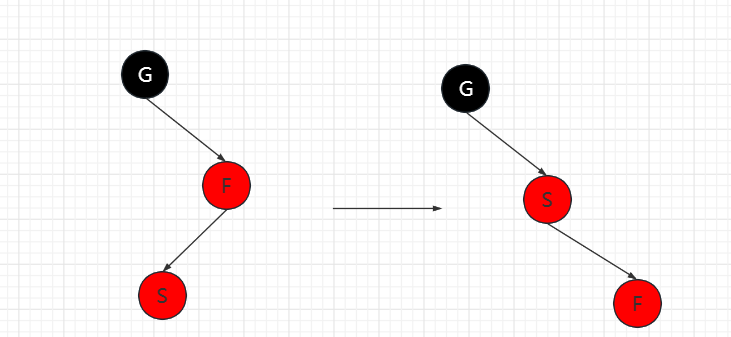
      • 插入节点为父节点的左节点（RL红）

        对F节点进行右旋，设置F节点为插入节点。此时便转换为RR红

        

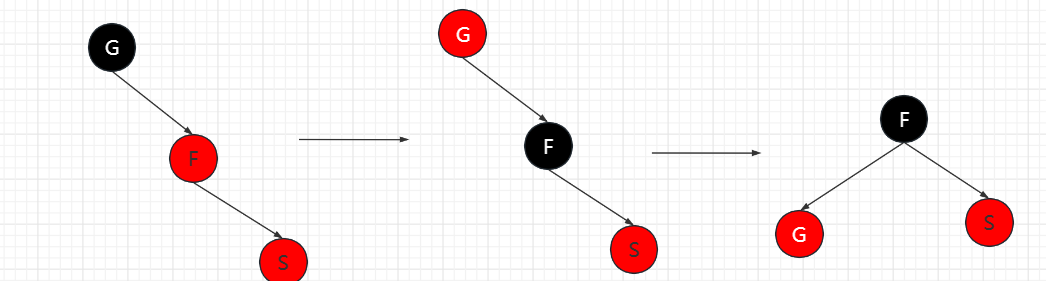
      • 插入节点为父节点的右节点（RR红）

        F节点变为黑色，G节点变为红色，对G节点进行左旋

        

参考资料

https://blog.csdn.net/chen_zhang_yu/article/details/52415077?utm_medium=distribute.pc_relevant.none-task-blog-baidujs_title

https://www.bilibili.com/video/BV1UJ411J7CU?p=4&vd_source=f6a308f875296edd5f437b68e0c3253a