网络瘤
前言:关于网络流有个生动的比喻,想象一个自来水厂向各处供水,自来水厂有无限多的水,但每条管子单位时间内允许的最大流量有限,现在钦定一个出水口为汇点,现在要做的就是在满足每一条管子不爆的情况下,最大化汇点流出的水量。
一、几个定义
1.网络
对于有向图 \(G=(V,E)\),其中每条边 \((u,v)\in E\) 都有权值 \(w(u,v)\),称之为容量,图中有两个特殊的点 \(s,t(s\not =t)\),称 \(s\) 为源点,\(t\) 为汇点,这个图称为网络。
2.流
对于任意的 \((u,v)\in E\),称 \(f(u,v)\) 为 \((u,v)\) 边的流量,\(f(u,v)\) 恒满足:
(1) \(f(u,v)\le w(u,v)\),即一条边的流量不能超过其容量。
(2) 若 \((v,u)\in E\),则 \(f(u,v)=-f(v,u)\),即一条边的流量与其相反边的流量互为相反数(注意不是反向边,反向边与相反边的区别是反向边 \((v,u)\notin E\))。
(3) \(\forall x\in E-\{s,t\},\sum_{(u,x)\in E}f(u,x)=\sum_{(x,v)\in E}f(x,v)\),即流入一个点的流量等于流出这个点的流量。
3.残量网络
对于所有的 \(w(u,v)-f(u,v)>0\) 的边组成的网络,称其为残量网络,残量网络中的边可能不属于 \(E\),具体原因等下解释。
4.增广路
在原图 \(G\) 或其某一个残量网络中,一条每条边的剩余容量都大于 \(0\) 的从 \(s\) 到 \(t\) 的路径,称为一条增广路。
二、最大流
这就是前言中所提到的那个问题了。
一个比较容易想到的思路是,不断地在残量网络中找寻增广路,直到没有增广路,此时的总流量即为最大流,但这个做法有点问题,例如下面这张图:
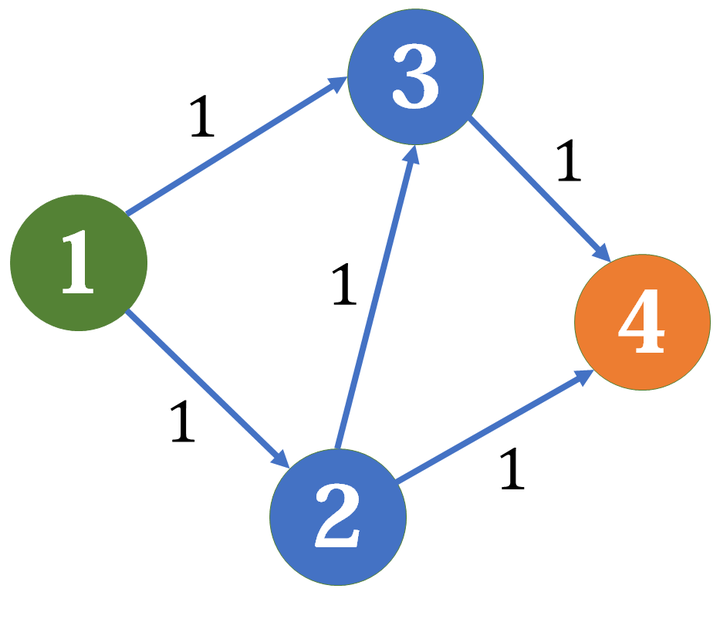
我们假设第一次增广,找到了 \(1->2->3->4\) 这条边,于是残量网络变成了这样:
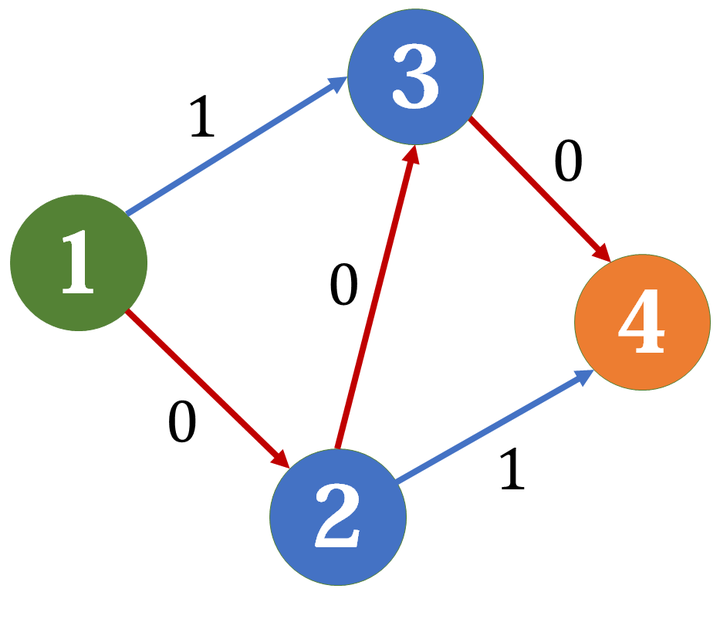
这里做了个近似,我们直接把边的容量改为其残余容量。
此时已经无法继续增广了,算法结束,但不难发现,其实走 \(1->3->4\) 和 \(1->2->4\) 总流量为 \(2\),这更优。
那怎么办?
我们考虑给程序一个反悔的机会,也就是说,建立一种方法,使得已经流过了某条边的流量再流回去,也就是建立反向边,为了保持总容量不变,反向边初始容量为 \(0\)。
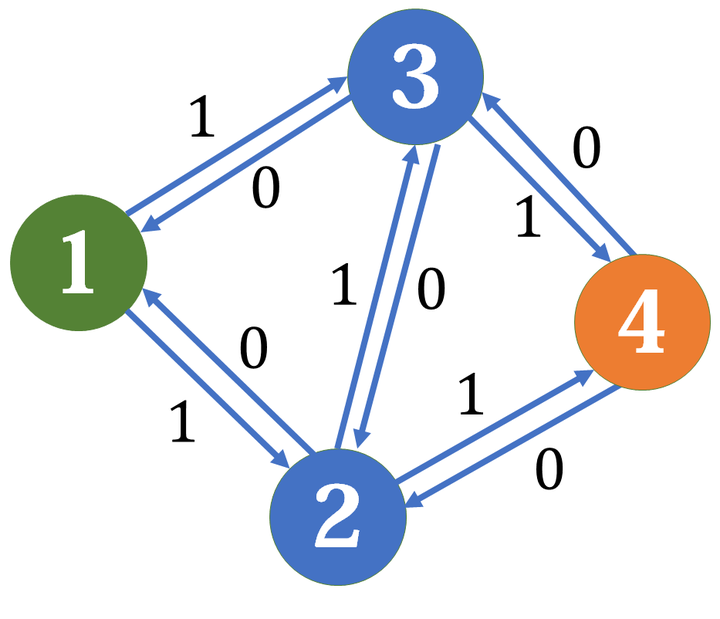
那么这时如果再走 \(1->2->3->4\),残量网络就变成了这样:
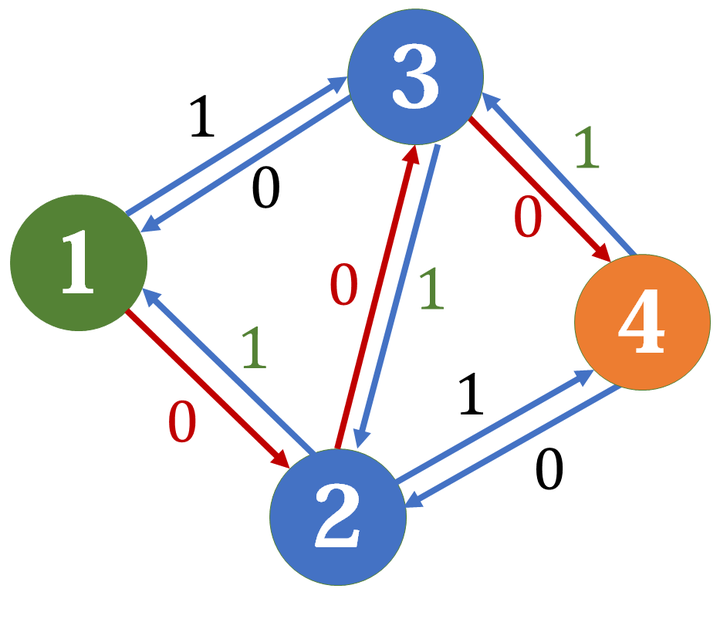
依然是为了保持总容量不变,在扣除正向边容量的同时,要给反向边加上相等的容量。
这时还可以继续增广:走 \(1->3->2->4\),惊奇的发现,\(2\) 给 \(3\) 的流量又让 \(3\) 给退回去了!而此时相当于选择了两条路径:\(1->3->4\) 和 \(1->2->4\),总流量为 \(2\),得到了正确的结果。
算法一、FF算法
最暴力的最大流算法,每次直接dfs找增广路,找不到了就完成。
#include<bits/stdc++.h>
#define ll long long
//#define int long long
#define lc(k) k<<1
#define rc(k) k<<1|1
using namespace std;
const int MAX=1e5+10;
const int MOD=1e9+7;
inline char readchar() {
static char buf[100000], *p1 = buf, *p2 = buf;
return p1 == p2 && (p2 = (p1 = buf) + fread(buf, 1, 100000, stdin), p1 == p2) ? EOF : *p1++;
}
inline int read() {
#define readchar getchar
int res = 0, f = 0;
char ch = readchar();
for(; !isdigit(ch); ch = readchar()) if(ch == '-') f = 1;
for(; isdigit(ch);ch = readchar()) res = (res << 1) + (res << 3) + (ch ^ '0');
return f ? -res : res;
}
inline void write(int x) {
if(x<0){putchar('-');x=-x;}
if(x>9) write(x/10);
putchar(x%10+'0');
}
int n,m,be,en;
struct node{int v,w,inv;};//由于是vector存图,所以需要整一个变量专门记录反向边
vector<node> s[MAX];
int vis[MAX];
int dfs(int k=be,int flow=1e9)
{
if(k==en) return flow;
vis[k]=1;
for(node &v:s[k])
{
int c;
if(v.w>0&&!vis[v.v]&&((c=dfs(v.v,min(v.w,flow)))!=-1))
{
v.w-=c;//本边剩余流量-c
s[v.v][v.inv].w+=c;//反边流量+c
return c;//找到增广路了
}
}
return -1;//找不到增广路了,算法结束
}
int FF()
{
int ans=0,c;
while((c=dfs())!=-1)
{
memset(vis,0,sizeof vis);
ans+=c;
}
return ans;
}
signed main()
{
n=read(),m=read(),be=read(),en=read();
for(int i=1;i<=m;i++)
{
int u=read(),v=read(),w=read();
s[u].push_back((node){v,w,(int)s[v].size()});//两边互为反向边
s[v].push_back((node){u,0,(int)s[u].size()-1});
}
cout<<FF();
return 0;
}
该算法的复杂度上界为 \(O(ef)\) ,\(e\) 为边数,\(f\) 为最大流(艹我怎么知道怎么推的),慢的一匹,模板题都过不去:

考虑这个算法为啥这么慢,主要原因还是dfs好绕远路,每次找到的不是最短的增广路,所以复杂度没有保障。
你dfsT飞了你会想啥?
正常人应该都会想到bfs,
于是就有了EK算法。
算法二、EK算法
如上所述,EK就是bfs版的FF算法。
但是由于没有了系统栈的加持,我们只能另开一个数组来存路径,具体看代码:
由于vector写EK很麻烦,于是我用了前向星。
//事实证明网络流还是用链式前向星吧
#include<bits/stdc++.h>
#define ll long long
#define int long long
#define lc(k) k<<1
#define rc(k) k<<1|1
using namespace std;
const int MAX=1.2e5+10;
const int MOD=1e9+7;
inline char readchar() {
static char buf[100000], *p1 = buf, *p2 = buf;
return p1 == p2 && (p2 = (p1 = buf) + fread(buf, 1, 100000, stdin), p1 == p2) ? EOF : *p1++;
}
inline int read() {
#define readchar getchar
int res = 0, f = 0;
char ch = readchar();
for(; !isdigit(ch); ch = readchar()) if(ch == '-') f = 1;
for(; isdigit(ch);ch = readchar()) res = (res << 1) + (res << 3) + (ch ^ '0');
return f ? -res : res;
}
inline void write(int x) {
if(x<0){putchar('-');x=-x;}
if(x>9) write(x/10);
putchar(x%10+'0');
}
int n,m,be,en,cnt=1;
int vis[MAX],let[MAX],flow[MAX];
int head[MAX];
struct node{int net,to,w;}edge[MAX<<1];
void add(int u,int v,int w)
{
edge[++cnt]=(node){head[u],v,w};
head[u]=cnt;
return ;
}
int bfs()
{
memset(let,0,sizeof let);
queue<int> q;
q.push(be);
flow[be]=1e9;
while(!q.empty())
{
int ff=q.front();
q.pop();
if(ff==en) break;
for(int i=head[ff];i;i=edge[i].net)
{
int v=edge[i].to,w=edge[i].w;
if(w>0&&!let[v])
{
let[v]=i;
flow[v]=min(flow[ff],w);
q.push(v);
}
}
}
return let[en];
}
int EK()
{
int mx=0;
while(bfs())
{
mx+=flow[en];
for(int i=en;i!=be;i=edge[let[i]^1].to)
{
edge[let[i]].w-=flow[en];
edge[let[i]^1].w+=flow[en];
}
}
return mx;
}
signed main()
{
n=read(),m=read(),be=read(),en=read();
for(int i=1;i<=m;i++)
{
int u=read(),v=read(),w=read();
add(u,v,w);add(v,u,0);
}
cout<<EK();
return 0;
}
该算法复杂度上界为 \(O(ve^2)\),但我们都知到一般的网络流都是跑不满的,所以他能过模板题。
好像还跑的挺快(大误)?

但是本着精益求精防毒瘤出题人的精神,这个算法还得继续优化。
三、Dinic算法
然而,最常用的网络流算法是Dinic算法。作为FF/EK算法的优化,它选择了先用BFS分层,再用DFS寻找。它的时间复杂度上界是 \(O(v^2e)\) 。
所谓分层,其实就是预处理出源点到每个点的距离(注意每次循环都要预处理一次,因为有些边可能容量变为 \(0\) 不能再走)。我们只往层数高的方向增广,可以保证不走回头路也不绕圈子。
我们可以使用多路增广节省很多花在重复路线上的时间:在某点DFS找到一条增广路后,如果还剩下多余的流量未用,继续在该点DFS尝试找到更多增广路。
此外还有当前弧优化。因为在Dinic算法中,一条边增广一次后就不会再次增广了,所以下次增广时不需要再考虑这条边。我们把head数组复制一份,但不断更新增广的起点。
#include<bits/stdc++.h>
#define ll long long
#define int long long
#define lc(k) k<<1
#define rc(k) k<<1|1
using namespace std;
const int MAX=1e5+10;
const int MOD=1e9+7;
inline char readchar() {
static char buf[100000], *p1 = buf, *p2 = buf;
return p1 == p2 && (p2 = (p1 = buf) + fread(buf, 1, 100000, stdin), p1 == p2) ? EOF : *p1++;
}
inline int read() {
#define readchar getchar
int res = 0, f = 0;
char ch = readchar();
for(; !isdigit(ch); ch = readchar()) if(ch == '-') f = 1;
for(; isdigit(ch);ch = readchar()) res = (res << 1) + (res << 3) + (ch ^ '0');
return f ? -res : res;
}
inline void write(int x) {
if(x<0){putchar('-');x=-x;}
if(x>9) write(x/10);
putchar(x%10+'0');
}
int n,m,be,en,cnt=1;
int vis[MAX],let[MAX],flow[MAX];
int head[MAX],dep[MAX],cur[MAX];
struct node{int net,to,w;}edge[MAX<<1];
void add(int u,int v,int w)
{
edge[++cnt]=(node){head[u],v,w};
head[u]=cnt;
return ;
}
bool bfs()
{
queue<int> q;
memset(dep,0,sizeof dep);
dep[be]=1;
q.push(be);
while(!q.empty())
{
int ff=q.front();q.pop();
for(int i=head[ff];i;i=edge[i].net)
if(!dep[edge[i].to]&&edge[i].w)
{
dep[edge[i].to]=dep[ff]+1;
q.push(edge[i].to);
if(edge[i].to==en) return 1;//分层完毕
}
}
return 0;//没搜到汇点,没有增广路了
}
int dfs(int k,int mf)//mf代表当前节点现在能够供给的最大流量
{
if(k==en) return mf;
int sum=0;
for(int i=cur[k];i;i=edge[i].net)//多路增广
{
cur[k]=i;//当前弧优化,本次dfs的下次访问直接从当前弧开始
int v=edge[i].to,&w=edge[i].w;
if(dep[v]==dep[k]+1&&w)//分层限制递归层数
{
int f=dfs(v,min(mf,w));
sum+=f;mf-=f;
w-=f;edge[i^1].w+=f;
if(mf==0) break;//该节点没有流量了,停止遍历
}
}
if(sum==0) dep[k]=0;//若该节点到不了汇点,将深度置为0,防止下次再次访问
return sum;
}
int Dinic()
{
int ans=0;
while(bfs())
{
memcpy(cur,head,sizeof head);//把head弧拷贝到当前弧去
ans+=dfs(be,1e9);
}
return ans;
}
signed main()
{
n=read(),m=read(),be=read(),en=read();
for(int i=1;i<=m;i++)
{
int u=read(),v=read(),w=read();
add(u,v,w);add(v,u,0);
}
cout<<Dinic();
return 0;
}
优化效果很可观:

另外提一下,Dinic在二分图上的复杂度是 \(O(n\sqrt e)\),优于匈牙利算法。
此外,还有一些求最大流的算法,如ISAP,预流推进等,有兴趣可以了解一下(艹,谁会有兴趣)。
三、最小割
给一些定义:
1.割:对于网络 \(G\),其割代表一种点的划分方式,这种划分方式需要满足将 \(G\) 恰好分为两部分 \(S,T\),且 \(s\in S\),\(t\in T\)。
2.割的容量:表示所有的从 \(S\) 到 \(T\) 的边的容量之和,即:\(w(S,T)=\sum_{u\in S,v\in T}w(u,v)\)。
3.最小割:容量最小的割即为最小割。
如何求最小割?
这里有一条定理,极其简洁的解决了这个问题:
最大流 \(=\) 最小割。
我们来试着证明下:
可以把最小割认为是将一些边割断,使得整个图分为 \(S\),\(T\) 两部分,那么容易得到图中所有的流量必定流经这些边中的某一条(否则无法从 \(s\) 到达 \(t\)),所以这些边的总流量 \(=\) 图的总流量。
而边的流量 \(\le\) 边的容量,
所以这些边的总流量 \(\le\) 这些边的总容量,
所以图的总流量 \(\le\) 这些边的总容量 ,
所以流 \(\le\) 割,
所以最大流 \(=\) 最小割。
那么求最小割实际上就是求最大流,这里不再赘述。
四、费用流
我们把前言里改一下,现在自来水厂想赚钱,于是每一单位的水流经某一条管时需要收取一定费用 \(c(u,v)\),但是为了惠民,自来水厂想找到一种方法,使得流最大的同时费用最小,这就是最小费用最大流。
回想一下前面的EK算法,我们找增广路时是随机找的,现在我不随机找了,我给每个点一个花费,我想要每次都在残量网络中找到花费最小的,咋办?
最短路。
有负权咋办?
spfa。
但它不是死了吗?
怎么会有出题人在负权图上卡spfa
#include<bits/stdc++.h>
#define ll long long
#define int long long
#define lc(k) k<<1
#define rc(k) k<<1|1
using namespace std;
const int MAX=1e5+10;
const int MOD=1e9+7;
inline char readchar() {
static char buf[100000], *p1 = buf, *p2 = buf;
return p1 == p2 && (p2 = (p1 = buf) + fread(buf, 1, 100000, stdin), p1 == p2) ? EOF : *p1++;
}
inline int read() {
#define readchar getchar
int res = 0, f = 0;
char ch = readchar();
for(; !isdigit(ch); ch = readchar()) if(ch == '-') f = 1;
for(; isdigit(ch);ch = readchar()) res = (res << 1) + (res << 3) + (ch ^ '0');
return f ? -res : res;
}
inline void write(int x) {
if(x<0){putchar('-');x=-x;}
if(x>9) write(x/10);
putchar(x%10+'0');
}
int head[MAX];
struct node{int to,net,w,c;}edge[MAX<<1];
int n,m,be,en,cnt=1,let[MAX],dis[MAX],flow[MAX],vis[MAX];
void add(int u,int v,int w,int c)
{
edge[++cnt]=(node){v,head[u],w,c};
head[u]=cnt;
return ;
}
bool spfa()
{
memset(let,0,sizeof let);
memset(flow,0,sizeof flow);
memset(vis,0,sizeof vis);
memset(dis,0x3f3f3f3f,sizeof dis);
queue<int> q;q.push(be);
dis[be]=0;vis[be]=1;flow[be]=1e9;
while(!q.empty())
{
int ff=q.front();q.pop();
vis[ff]=0;
// if(ff==en) break;
for(int i=head[ff];i;i=edge[i].net)
{
int v=edge[i].to,c=edge[i].c,w=edge[i].w;
if(dis[ff]+c<dis[v]&&w)//可松弛且残流不为0
{
let[v]=i;
dis[v]=dis[ff]+c;
flow[v]=min(w,flow[ff]);
if(!vis[v]) q.push(v),vis[v]=1;
}
}
}
return flow[en];
}
int ans1=0,ans2=0;
void EK()
{
while(spfa())
{
ans1+=flow[en];
ans2+=flow[en]*dis[en];
for(int i=en;i!=be;i=edge[let[i]^1].to)
{
edge[let[i]].w-=flow[en];
edge[let[i]^1].w+=flow[en];
}
}
return ;
}
signed main()
{
n=read(),m=read(),be=read(),en=read();
for(int i=1;i<=m;i++)
{
int u=read(),v=read(),w=read(),c=read();
add(u,v,w,c);add(v,u,0,-c);
}
EK();
cout<<ans1<<" "<<ans2;
return 0;
}
当然dijkstra也存在一种方法来处理负权图,但这超出了我们的讨论范围以及我的认知水平。
五、一点例题
鲁迅曾说过:网络流最难的是建图。我们通过几道例题来看一下究竟该怎么考虑。
标签:en,增广,int,MAX,网络,笔记,科技,edge,long From: https://www.cnblogs.com/wapmhac/p/16641647.html