树状数组

title: 树状数组
tags: 算法
date: 2022-11-28 13:36:11

本文章遵守知识共享协议 CC-BY-NC-SA ，转载时须在文章的任一位置附上原文链接和作者署名（rickyxrc）。推荐在我的个人博客阅读。

简介

树状数组是一种可以快速更改单点并查询区间和的一种数据结构。

为啥不用线段树？因为树状数组省空间。

又因为毒瘤出题人一般不卡空间，所以建议学学线段树。

前置知识

• 位运算
• 树（只有一点点）
• 差分（改进会用到）

讲解

大概是长这个样子的：

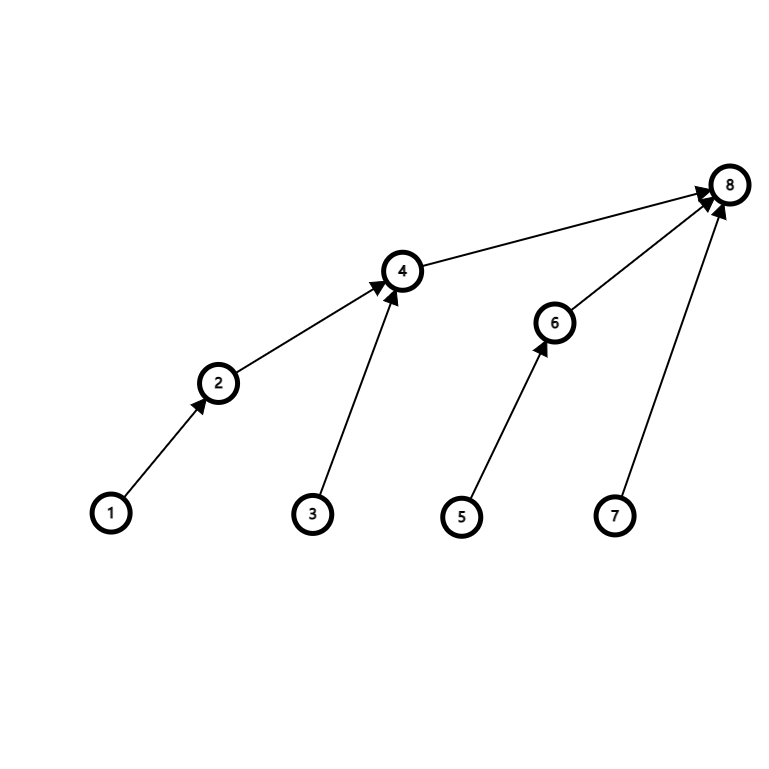
树状数组的核心在于这个函数：

int lowbit(int x){
    return x&(-x);
}

根据位运算的一些知识，我们可以得到这个函数的作用是求一个数字最右边的 \(1\) 所代表的数值。

感性的理解一下，当前节点为 \(i\) ，父亲就为 \(i+lowbit(i)\)。

这样可以很快写出查询和修改的代码。

int query(int index){ // 查询 [1,n]
    int ans=0;
    while(index>0){
        ans+=data[index];
        index-=lowbit(index);
    }
    return ans;
}
void update(int index,int val){ // 单点更改
    while(index<=n){
        data[index]+=val;
        index+=lowbit(index);
    }
}

例题

温馨提示：树状数组的题线段树都可以做，对于例题，建议直接去看线段树

P3374-【模板】树状数组-1

直接套模板。

P3368-【模板】树状数组-2

这里会用到差分的知识，如果不理解可以看看还没写出来的差分的文章。

直接将原数组差分，然后查询就行。