[SCOI2011]地板
题目描述
lxhgww 的小名叫“小 L”,这是因为他总是很喜欢 L 型的东西。
小 L 家的客厅是一个 \(r\times c\) 的矩形,现在他想用 L 型的地板来铺满整个客厅,客厅里有些位置有柱子,不能铺地板。
现在小 L 想知道,用 L 型的地板铺满整个客厅有多少种不同的方案?
需要注意的是,如下图所示,L 型地板的两端长度可以任意变化,但不能长度为 \(0\)。
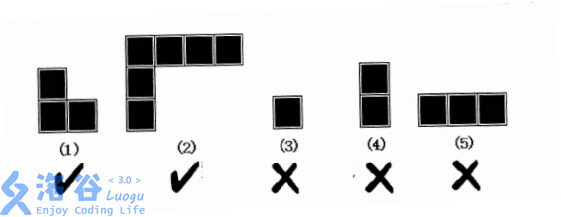
铺设完成后,客厅里面所有没有柱子的地方都必须铺上地板,但同一个地方不能被铺多次。
输入格式
输入的第一行包含两个整数,\(r\) 和 \(c\),表示客厅的大小。
接着是 \(r\) 行,每行 \(c\) 个字符,字符要么是 _,要么是 *,_ 表示对应的位置是空的,必须铺地板;* 表示对应的位置有柱子,不能铺地板。
输出格式
输出一行,包含一个整数,表示铺满整个客厅的方案数。由于这个数可能很大,只需输出它除以 \(20110520\) 的余数。
样例 #1
样例输入 #1
2 2
*_
__
样例输出 #1
1
样例 #2
样例输入 #2
3 3
___
_*_
___
样例输出 #2
8
提示
数据规模与约定
| 测试点编号 | 数据限制 |
|---|---|
| \(1\sim 2\) | \(1\le r\times c\le 25\) |
| \(3\sim 5\) | \(1\le r\times c\le 100\) 并且 (\(r=2\) 或者 \(c=2\)) |
| \(6\sim 10\) | \(1\le r\times c\le 100\) |
Solution
心态写崩了的一道题,不过既然是插头 DP,那还是值得写一写的。如果你不知道插头 DP,请移步模板题。
与模板题不相同的是,本题的路径是 L 型的,所以就不能够按照模板中插头的定义来做,这时候我们就需要将插头的定义进行更改:\(1\) 表示没到转折点的时候的插头,\(2\) 表示过了转折点后的插头,\(0\) 则是无插头。如果你对插头 DP 足够的熟悉,其实到了这里就可以尝试自己先推一推转移的方程了。如果你推完了,或者说是对插头 DP 并不熟,那就接着往下看吧:
为了方便书写,定义 \(isR\) 为当前格子左侧轮廓线的插头,\(isD\) 为当前格子上侧轮廓线的插头。
分类讨论
1. 当前格子为障碍格
很明显,这种情况的处理方式与模板题相同,如果当前格子不具有左插和上插(\(isR=isD=0\)),那么就是一个合法的状态,可以进行转移。
2. 左插和上插都为 \(1\)(\(isD=isR=1\))
\[\begin{matrix} & \downarrow_1\\ \rightarrow_1 & \square \end{matrix} \]当前格子肯定只有一种选择,就是作为 L 的拐点,所以下一个状态就是将这两个插头删除(组成了 L 型,这两个插头也就不存在了):
\[\begin{matrix} &\downarrow_1\\ \rightarrow_1 & \square &0\\ &0 \end{matrix} \]3. 左插上插都不存在(\(isR=isD=0\))
\[\begin{matrix} & 0\\ 0 & \square \end{matrix} \]当前格子此时可以作为 L 型的一个起点,也就是说右插为 \(1\) 或是下插为 \(1\):
\[\begin{matrix} &0\\ 0& \square & \rightarrow_1\\ &0 \end{matrix} \]或者是
\[\begin{matrix} &0\\ 0&\square & 0\\ &\downarrow_1 \end{matrix} \]同时也可以作为 L 型的拐点,右插为 \(2\) 并且下插为 \(2\):
\[\begin{matrix} &0\\ 0& \square & \rightarrow_2\\ &\downarrow_2 \end{matrix} \]4. 左插为 \(1\),上插为 \(0\)(\(isR=1,isD=0\))
\[\begin{matrix} & 0\\ \rightarrow_1 & \square \end{matrix} \]当前格子此时可以作为 L 型一条边上的一部分,即右插为 \(1\):
\[\begin{matrix} &0\\ \rightarrow_1&\square & \rightarrow_1\\ &0 \end{matrix} \]也可以作为 L 型的拐点,即下插为 \(2\):
\[\begin{matrix} & 0\\ \rightarrow_1 & \square &0\\ & \downarrow_2 \end{matrix} \]5. 左插为 \(0\),上插为 \(1\)(\(isR=0,isD=1\))
此种情况与第 \(4\) 种近乎相同,就不再赘述。
6. 左插为 \(2\),上插为 \(0\)(\(isR=2,isD=0\))
\[\begin{matrix} &0\\ \rightarrow_2 & \square \end{matrix} \]当前格子此时可以作为 L 型的另一边继续拓展,即右插为 \(2\):
\[\begin{matrix} &0\\ \rightarrow_2 & \square & \rightarrow_2\\ &0 \end{matrix} \]也可以作为这条边的终点,即不具有下插和右插:
\[\begin{matrix} &0\\ \rightarrow_2 & \square & 0\\ &0 \end{matrix} \]7. 左插为 \(0\),上插为 \(2\)(\(isR=0,isD=2\))
这种情况与第 \(6\) 种大体相同。
另外需要注意题目输入中只给出了 \(r\times c\) 的大小,并没有给出具体某一维的大小,所以需要将小的那一维来进行状态压缩,以避免超过 \(64\) 位限制。因为 \(r \times c\le 100\),所以可以知道如果压缩小的一维,最多只会只有 \(10\) 位(我采用的四进制压缩)。
为了减少无用的状态数,可以选用哈希表来优化空间。但即使如此也会因为格子数较多而导致空间极大,所以可以采用滚动数组的办法来优化。
Code
代码中的状态转移部分是与上面分类的情况按顺序一一对应的,所以代码中就不会再进行解释了。
#include<bits/stdc++.h>
#define int long long
#define mem(a,b) memset(a,b,sizeof a)
using namespace std;
template<typename T> void read(T &k)
{
k=0;T flag=1;char b=getchar();
while (!isdigit(b)) {flag=(b=='-')?-1:1;b=getchar();}
while (isdigit(b)) {k=k*10+b-48;b=getchar();}
k*=flag;
}
template<typename T> void write(T k) {if (k<0) {putchar('-'),write(-k);return;}if (k>9) write(k/10);putchar(k%10+48);}
template<typename T> void writewith(T k,char c) {write(k);putchar(c);}
int n,m;
bool mp[105][105];
int pre=1,cur=0;//用于滚动
const int _MAXN=6e5,mod=20110520,HSIZE=590027;
int f[2][_MAXN+5],bits[105],ex,ey;
int state[2][_MAXN+5],tot[2],ptr[_MAXN+5],at=0;
struct HASH{
int pre,to;
}H[_MAXN+5];
void modify(int sta,int val)//加入Hash表
{
int key=sta%HSIZE;
for (int i=ptr[key];i;i=H[i].pre)
if (state[cur][H[i].to]==sta)//有这个状态
{
f[cur][H[i].to]=(f[cur][H[i].to]+val)%mod;//最开始这个地方取模写成对hash大小取模了,检查了一个小时……
return;
}
tot[cur]++;//没有这个状态,加入hash表
state[cur][tot[cur]]=sta;
f[cur][tot[cur]]=val%mod;
H[++at].to=tot[cur];
H[at].pre=ptr[key];
ptr[key]=at;
}
int Fans=0;
void init() {for (int i=1;i<=100;i++) bits[i]=i<<1;}//方便取对应位置
void PlugDP()
{
tot[cur]=1;f[cur][1]=1;state[cur][1]=0;
for (int i=1;i<=n;i++)
{
for (int j=1;j<=tot[cur];j++) state[cur][j]<<=2;//将轮廓线下移
for (int j=1;j<=m;j++)
{
swap(cur,pre);//滚动数组
at=0,tot[cur]=0;mem(ptr,0);//清空hash表
for (int k=1;k<=tot[pre];k++)
{
int nowans=f[pre][k],nowsta=state[pre][k];
int isR=(nowsta>>bits[j-1])%4,isD=(nowsta>>bits[j])%4;
if (!mp[i][j])//1
{
if ((!isD) && (!isR)) modify(nowsta,nowans);
}
else if (isR==1 && isD==1)//2
{
if (i==ex && j==ey) Fans=(Fans+nowans)%mod;
modify(nowsta-(1<<bits[j])-(1<<bits[j-1]),nowans);
}
else if ((!isR) && (!isD))//3
{
if (mp[i+1][j]) modify(nowsta+(1<<bits[j-1]),nowans);
if (mp[i][j+1]) modify(nowsta+(1<<bits[j]),nowans);
if (mp[i+1][j] && mp[i][j+1]) modify(nowsta+2*(1<<bits[j-1])+2*(1<<bits[j]),nowans);
}
else if (isR==1 && (!isD))//4
{
if (mp[i][j+1]) modify(nowsta-(1<<bits[j-1])+(1<<bits[j]),nowans);
if (mp[i+1][j]) modify(nowsta+(1<<bits[j-1]),nowans);
}
else if ((!isR) && isD==1)//5
{
if (mp[i+1][j]) modify(nowsta-(1<<bits[j])+(1<<bits[j-1]),nowans);
if (mp[i][j+1]) modify(nowsta+(1<<bits[j]),nowans);
}
else if ((!isR) && isD==2)//6
{
if (i==ex && j==ey) Fans=(Fans+nowans)%mod;
if (mp[i+1][j]) modify(nowsta-2*(1<<bits[j])+2*(1<<bits[j-1]),nowans);
modify(nowsta-2*(1<<bits[j]),nowans);
}
else if (isR==2 && (!isD))//7
{
if (i==ex && j==ey) Fans=(Fans+nowans)%mod;
if (mp[i][j+1]) modify(nowsta-2*(1<<bits[j-1])+2*(1<<bits[j]),nowans);
modify(nowsta-2*(1<<bits[j-1]),nowans);
}
}
}
}
}
signed main()
{
init();
read(n),read(m);
if (n>=m)//如果m小就不转矩阵
{
for (int i=1;i<=n;i++)
{
char st[105];scanf("%s",st+1);
for (int j=1;j<=m;j++) if (st[j]=='_') mp[i][j]=1;
}
}
else //将n转到m的位置
{
swap(n,m);
for (int i=1;i<=m;i++)
{
char st[105];scanf("%s",st+1);
for (int j=1;j<=n;j++) if (st[j]=='_') mp[j][i]=1;
}
}
for (int i=1;i<=n;i++)
for (int j=1;j<=m;j++)
if (mp[i][j]) ex=i,ey=j;//转置后寻找最后一个非障碍点来统计答案,因为我最开始就是这个点找错了所以就直接提到读入外面来统一寻找了
PlugDP();
writewith(Fans,'\n');
return 0;
}