标签：队列 新生 back 选手 栈是 区间 单调

算法学习笔记(66): 单调队列

https://zhuanlan.zhihu.com/p/346354943

“如果一个选手比你小还比你强，你就可以退役了。”——单调队列的原理

好久没写笔记了，先补一个简单的。单调队列是一种主要用于解决滑动窗口类问题的数据结构，即，在长度为 n 的序列中，求每个长度为 m 的区间的区间最值。它的时间复杂度是 O(n) ，在这个问题中比 O(nlog⁡n) 的ST表和线段树要优。

单调队列的基本思想是，维护一个双向队列（deque），遍历序列，仅当一个元素可能成为某个区间最值时才保留它。

形象地打个比方，上面的序列可以看成学校里各个年级XCPC选手，数字越大代表能力越强。每个选手只能在大学四年间参赛，毕业了就没有机会了。那么，每一年的王牌选手都在哪个年级呢？

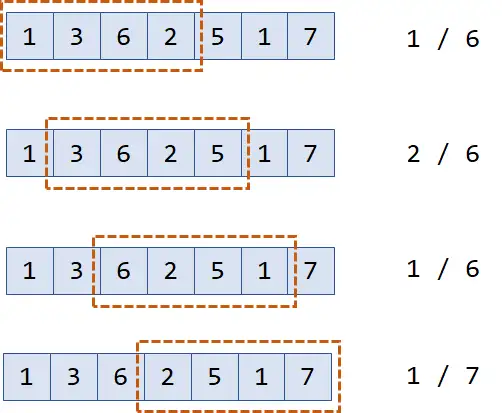
一开始的时候，大三大四的学长都比较菜，大二的最强，而大一的等大二的毕业后还有机会上位，所以队列里有两个数。

一年过去了，原本大一的成为大二，却发现新进校的新生非常强，自己再也没有机会成为最大值了，所以弹出队列。

又过了一年，新入校的新生尽管能力只有1，但理论上只要后面的人比他还菜，还是可能成为区间最大值的，所以入队。

终于，原本的王牌毕业了，后面的人以为熬出头了，谁知道这时一个巨佬级别的新生进入了集训队，这下其他所有人都没机会了。

（这只是比方，现实中各位选手的实力是会增长的，不符合这个模型ovo）

总之，观察就会发现，我们维护的这个队列总是单调递减的。如果维护区间最小值，那么维护的队列就是单调递增的。这就是为什么叫单调队列。

代码也很简洁：

deque<int> Q; // 存储的是编号
for (int i = 0; i < n; ++i)
{
    if (!Q.empty() && i - Q.front() >= m) // 毕业
        Q.pop_front();
    while (!Q.empty() && V[Q.back()] < V[i]) // 比新生弱的当场退役（求区间最小值把这里改成>即可）
        Q.pop_back();
    Q.push_back(i); // 新生入队
    if (i >= m - 1)
        cout << V[Q.front()] << " ";
}

标签：队列,新生,back,选手,栈是,区间,单调
From： https://www.cnblogs.com/bonelee/p/16988251.html