\(\color{red}{注:以下只是个人总结,由于水平有限,基本是参考文献中的原文,感兴趣请看原文。}\)
1. 论文
相关论文目录:
- DDPM Denoising Diffusion Probabilistic Models
- Score-Based Generative Modeling through Stochastic Differential Equations
- Denoising Diffusion Implicit Models
- Diffusion Models Beat GANs on Image Synthesis
- Classifier-Free Diffusion Guidance
2. diffusion model解释
对diffusion mode 的数学解释,所有解释参考自 苏剑林 大佬的博客(\(\color{red}{感兴趣直接看原文}\))
2.1 DDPM=拆楼+建楼
原文地址
将DDPM看做渐变模型更加准确一点。
拆楼建楼
扩散模型的过程就是将一个随机噪声\(z\)变换成一个数据样本\(x\)的过程,如Fig.1所示, 将整个过程类比为拆楼建楼的过程。
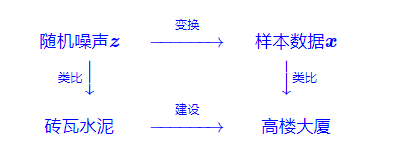
Fig.1
Source:
设\(x_0\)为建设好的高楼大厦(数据样本),\(x_T\)为拆好的砖瓦水泥(随机噪声),假设拆楼需要\(T\)步,整个过程可以表示为
\[\begin{equation}\boldsymbol{x} = \boldsymbol{x}_0 \to \boldsymbol{x}_1 \to \boldsymbol{x}_2 \to \cdots \to \boldsymbol{x}_{T-1} \to \boldsymbol{x}_T = \boldsymbol{z}\end{equation} \]将拆楼建楼分为多步,\(\boldsymbol{x}_{t-1} \to \boldsymbol{x}_t\)表示拆楼的下一步,\(\boldsymbol{x}_{t} \to \boldsymbol{x}_{t-1}\)就是建楼的下一步,如果我们知道二者之间的转换关系\(x_{t-1}=\mu(x_t)\),那么从\(x_T\)出发,反复执行\(x_{T-1} = \mu(x_T),...,x_{T-2}=\mu(x_{T-1})...\),最终就能得到高楼大厦\(x_0\)
该怎么拆
DDPM做生成模的过程,其实就是拆楼建楼的过程,先构造一个从数据样本渐变到随机噪声的过程,然后在考虑其逆变换,通过反复执行逆变换来完成数据样本的生成,所以说DDPM这种做法其实应该是“渐变模型”, 而不是“扩散模型”。
具体来说,DDPM将“拆楼“的过程建模为:
\[x_t=\alpha_tx_{t-1} + \beta_t\epsilon_t, \ \epsilon_t \sim \mathcal{N}(0, 1) \tag{1} \]其中有\(\alpha_t,\beta_t>0\)且\(\alpha_t^2+\beta_t^2=1, \beta_t\)通常很接近与0,代表这单步"拆楼"中对原来楼体的破坏程度,噪声\(\epsilon_t\) 的引入代表着对原始信号的一种破坏,我们也可以将它理解成为“原材料”,即每一步“拆楼”中我们都将\(x_{t-1}\)拆解成"\(\alpha_tx_{t-1}\)的楼体+\(\beta_t\epsilon_t\)的原料"。
反复执行这个拆楼的这个步骤,我们可以得到:
title: 为什么叠加的系数要满足$\alpha_t^2+\beta_t^2=1$
collapse: open
首先,公式中花括号所指出的部分,正好是多个独立的正态噪声之和,其均值为0,方差则分别为$(\alpha_t...\alpha_2)^2\beta_1^2$、$(\alpha_t...\alpha_3)^2\beta_2^2$、...、$\alpha_t^2\beta_{t-1}^2$、$\beta_t^2$;然后,利用概率论的知识--正态分布的叠加性,即上述多个独立的正态噪声之后的分布,实际上是均值为0,方差为$(\alpha_t...\alpha_2)^2\beta_1^2+(\alpha_t...\alpha_3)^2\beta_2^2+...+\alpha_t^2\beta_{t-1}^2+\beta_t^2$的正态分布;最后,在$\alpha_t^2+\beta_t^2=1$恒成立的情况下,我们可以得到(1)中的各项系数平方和依旧为1,即
$$
(\alpha_t...\alpha_1)^2+(\alpha_t...\alpha_2)^2\beta_1^2+(\alpha_t...\alpha_3)^2\beta_2^2+...+\alpha_t^2\beta_{t-1}^2+\beta_t^2=1
$$
所以实际上相当于有:
$$\boldsymbol{x}_{t}=\underbrace{\left(\alpha_{t} \cdots \alpha_{1}\right)}_{\text {记为 } \bar{\alpha}_{t}} \boldsymbol{x}_{0}+\underbrace{\sqrt{1-\left(\alpha_{t} \cdots \alpha_{1}\right)^{2}} \overline{\boldsymbol{\varepsilon}}_{t}}_{\text {记为 } \bar{\beta}_{t}}, \quad \overline{\boldsymbol{\varepsilon}}_{t} \sim \mathcal{N}(\mathbf{0}, \boldsymbol{I} \tag{5})$$
这就为计算$x_t$提供了极大的便利。另一方面,DDPM会选择适当的$\alpha_t$形式,使得有$\bar{\alpha}_T\approx 0$,这意味着经过$T$步的拆楼之后,所剩的楼体几乎可以忽略了,已经全部转化为原材料$\epsilon$。
又如何建
拆楼是\(x_{t-1}\longrightarrow x_t\) 的过程,这个过程我们得到很多的数据对\((x_{t-1},x_t)\) ,那么建楼自然就是从这些数据中学习一个\(x_{t}\longrightarrow x_{t-1}\)的模型。设该模型为\(\mu(x_t)\),那么容易想到的学习方案就是最小化二者的欧氏距离:
其实这已经非常接近最终的DDPM模型了,将过程更加精细化。首先"拆楼"的式(1)改写为\(x_{t-1}=\frac{1}{\alpha}(x_t-\beta_t\epsilon_t)\) ,这启发我们或许可以将“建楼”模型\(\mu(x_t)\)设计成
\[\mu(x_t)=\frac{1}{\alpha_t}(x_t-\beta_t\epsilon_{\theta}(x_t, t)) \tag{3} \]的形式,其中\(\theta\)是训练参数,将其代入损失函数中,得到:
\[\left \| x_{t-1}-\mu(x_t) \right \|^2=\frac{\beta_t^2}{\alpha_t^2}\left \| \epsilon_t-\epsilon_{\theta}(x_t,t) \right \|^2 \tag{4} \]前面的因子\(\frac{\beta_t^2}{\alpha_t^2}\)表示loss的权重,这个可以暂时忽略,最后代入(1)结合(5)给出\(x_t\)的表达式
\[x_t=\alpha_tx_{t-1}+\beta_t\epsilon_t=\alpha_t(\bar{\alpha}_{t-1}x_0+\bar{\beta}_{t-1}\bar{\epsilon}_{t-1})+\beta_t\epsilon_t=\bar{\alpha}_tx_0+\alpha_t\bar{\beta}_{t-1}\bar{\epsilon}_{t-1}+\beta_t\epsilon_t \tag{6} \]得到损失函数的形式为
\[\left \| \epsilon_t-\epsilon_{\theta}(\bar{\alpha}_tx_0+\alpha_t\bar{\beta}_{t-1}\bar{\epsilon}_{t-1}+\beta_t\epsilon_t,t) \right \|^2 \tag{7} \]title:为什么要退一步来给出$x_t$,直接根据式(5)来给出$x_t$可以吗?
答案是不行的,因为我们已经事先采样了$\epsilon_t$,而$\epsilon_t$跟$\bar{\epsilon}_t$不是相互独立的,所以给定$\epsilon_t$的情况下,我们不能完全独立地采样$\epsilon_t$
降低方差
原则上说,损失函数(7)就可以完成DDPM的训练了,但他在实践中可能有方差过大的风险,从而导致收敛过慢等问题。因为(7)实际上包含了4个需要采样的随机变量
1. 从所有训练样本中采样一个$x_0$;
2. 从正态分布$\mathcal{N}(0,1)$中采样$\bar{\epsilon}_{t-1},\epsilon_t$(两个不同的采样结果);
3. 从$1 \sim T$中采样一个$t$。
要采样的随机变量越多,就越难对损失函数做精确的估计,反过来说就是每次对损失函数进行估计的波动(方差)过大了。很幸运的是,可以通过一个积分技巧来将\(\bar{\epsilon}_{t-1},\epsilon_t\)和并成单个正态随机变量,从而缓解一下方差大的问题。
由于正态分布的叠加性,我们知道\(\alpha_t\bar{\beta}_{t-1}\bar{\epsilon}_{t-1}+\beta_t\epsilon_t\)实际上相当于单个随机变量\(\bar{\beta}_t\epsilon|\epsilon\sim \mathcal{N}(0,1)\),同理\(\beta_t\bar{\epsilon}_{t-1}-\alpha_t\bar{\beta}_{t-1}\epsilon_t\)实际上相当于单个随机变量\(\bar{\beta}_t\omega |\omega \sim \mathcal{N}(0,1)\) ,并且我们可以验证\(\mathbb{E}[\epsilon\omega^T]=0\),所以这是两个相互独立的正态随机变量。
接下来,反过来将\(\epsilon_t\)用\(\epsilon,\omega\)重新表示出来:
\[\begin{equation}\boldsymbol{\varepsilon}_t = \frac{(\beta_t \boldsymbol{\varepsilon} - \alpha_t\bar{\beta}_{t-1} \boldsymbol{\omega})\bar{\beta}_t}{\beta_t^2 + \alpha_t^2\bar{\beta}_{t-1}^2} = \frac{\beta_t \boldsymbol{\varepsilon} - \alpha_t\bar{\beta}_{t-1} \boldsymbol{\omega}}{\bar{\beta}_t}\end{equation} \tag{8} \]代入(7)得到
\[\begin{equation}\begin{aligned} &\,\mathbb{E}_{\bar{\boldsymbol{\varepsilon}}_{t-1}, \boldsymbol{\varepsilon}_t\sim \mathcal{N}(\boldsymbol{0}, \boldsymbol{I})}\left[\left\Vert \boldsymbol{\varepsilon}_t - \boldsymbol{\epsilon}_{\boldsymbol{\theta}}(\bar{\alpha}_t\boldsymbol{x}_0 + \alpha_t\bar{\beta}_{t-1}\bar{\boldsymbol{\varepsilon}}_{t-1} + \beta_t \boldsymbol{\varepsilon}_t, t)\right\Vert^2\right] \\ =&\,\mathbb{E}_{\boldsymbol{\omega}, \boldsymbol{\varepsilon}\sim \mathcal{N}(\boldsymbol{0}, \boldsymbol{I})}\left[\left\Vert \frac{\beta_t \boldsymbol{\varepsilon} - \alpha_t\bar{\beta}_{t-1} \boldsymbol{\omega}}{\bar{\beta}_t} - \boldsymbol{\epsilon}_{\boldsymbol{\theta}}(\bar{\alpha}_t\boldsymbol{x}_0 + \bar{\beta}_t\boldsymbol{\varepsilon}, t)\right\Vert^2\right] \end{aligned}\end{equation} \tag{9} \]注意到,现在损失函数关于\(\omega\)只是二次的,所以我们可以展开然后将它的期望直接算出来,结果是:
\[\begin{equation}\frac{\beta_t^2}{\bar{\beta}_t^2}\mathbb{E}_{\boldsymbol{\varepsilon}\sim \mathcal{N}(\boldsymbol{0}, \boldsymbol{I})}\left[\left\Vert\boldsymbol{\varepsilon} - \frac{\bar{\beta}_t}{\beta_t}\boldsymbol{\epsilon}_{\boldsymbol{\theta}}(\bar{\alpha}_t\boldsymbol{x}_0 + \bar{\beta}_t\boldsymbol{\varepsilon}, t)\right\Vert^2\right]+\text{常数}\end{equation} \tag{10} \]在此省掉常数和损失函数的权重,就可以得到DDPM最终所用的损失函数:
\[\begin{equation}\left\Vert\boldsymbol{\varepsilon} - \frac{\bar{\beta}_t}{\beta_t}\boldsymbol{\epsilon}_{\boldsymbol{\theta}}(\bar{\alpha}_t\boldsymbol{x}_0 + \bar{\beta}_t\boldsymbol{\varepsilon}, t)\right\Vert^2\end{equation}\tag{11} \]\(\color{red}{(提示:原论文中的\epsilon_{\theta}实际上就是本文的\frac{\bar{\beta}_t}{\beta_t}\boldsymbol{\epsilon}_{\boldsymbol{\theta}}})\)
递归生成
训练完之后,我们就可以通过一个随机噪声\(\boldsymbol{x}_T\sim\mathcal{N}(\boldsymbol{0}, \boldsymbol{I})\)出发执行\(T\)步式(3)来进行生成
这对应于自回归解码中的Greedy Search。如果要进行Random Sample,那么需要补上噪声项:
\[\begin{equation}\boldsymbol{x}_{t-1} = \frac{1}{\alpha_t}\left(\boldsymbol{x}_t - \beta_t \boldsymbol{\epsilon}_{\boldsymbol{\theta}}(\boldsymbol{x}_t, t)\right) + \sigma_t \boldsymbol{z},\quad \boldsymbol{z}\sim\mathcal{N}(\boldsymbol{0}, \boldsymbol{I})\end{equation}\tag{13} \]title: 对比传统郎之万采样
一般来说,我们可以让$\alpha_t=\beta_t$,即正向和反向的方差保持同步。这个采样过程跟传统扩散模型的朗之万采样不一样的地方在于:DDPM的采样每次都从一个随机噪声出发,需要重复迭代T步来得到一个样本输出;朗之万采样则是从任意一个点出发,反复迭代无限步,理论上这个迭代无限步的过程中,就把所有数据样本都被生成过了。所以两者除了形式相似外,实质上是两个截然不同的模型。
title:DDMP 问题
collapse: true
跟Seq2Seq的解码过程是一样的,都是串联式的自回归生成,所以生成速度是一个瓶颈,DDPM中$T=1000$,意味着每生成一个图片,需要将$\epsilon_{\theta}(x_t,t)$反复执行1000次,所以导致采样速度慢。
超参设置
在DDPM中,T=1000,为什么要设置这么大的T呢?对于\(\alpha_t\)的选择:
这是一个单调递减的函数,为什么要选择单调递减?
其实这两个问题有着相近的答案,跟具体的数据背景有关。简单起见,在重构的时候我们用了欧氏距离作为损失函数,而一般我们用DDPM做图片生成,以往做过图片生成的读者都知道,欧氏距离并不是图片真实程度的一个好的度量,VAE用欧氏距离来重构时,往往会得到模糊的结果,除非是输入输出的两张图片非常接近,用欧氏距离才能得到比较清晰的结果,所以选择尽可能大的T,正是为了使得输入输出尽可能相近,减少欧氏距离带来的模糊问题。
选择单调递减的\(\alpha_t\)也有类似考虑。当t比较小时,\(x_t\)还比较接近真实图片,所以我们要缩小\(x_{t-1}\)与\(x_t\)的差距,以便更适用欧氏距离,因此要用较大的\(\alpha_t\);当t比较大时,\(x_t\)已经比较接近纯噪声了,噪声用欧式距离无妨,所以可以稍微增大\(x_t\)与\(x_t\)的差距,即可以用较小的\(\alpha_t\)。那么可不可以一直用较大的\(\alpha_t\)呢?可以是可以,但是要增大T。注意在推导时,我们说过应该有\(\bar{alpha}_T\approx 0\),而我们可以直接估算
\[\begin{equation}\log \bar{\alpha}_T = \sum_{t=1}^T \log\alpha_t = \frac{1}{2} \sum_{t=1}^T \log\left(1 - \frac{0.02t}{T}\right) < \frac{1}{2} \sum_{t=1}^T \left(- \frac{0.02t}{T}\right) = -0.005(T+1)\end{equation} \]代入\(T=1000\)大致是\(\bar{\alpha}_T\approx e^{-5}\),这个其实就刚好达到\(\approx0\)的标准。所以如果从头到尾都用较大的\(\alpha_t\)那么必然需要更大的T才行。
2.2 DDPM=自回归式VAE
原文地址:生成扩散模型漫谈(二):DDPM = 自回归式VAE
多步突破
在传统的VAE中,编码过程和生成过程都是一步到位的:
这样做就只涉及到三个分布:编码分布\(p(z|x)\)、生成分布\(q(x|z)\)、以及先验分布\(q(z)\),它的好处是形式比较简单,\(x\)和\(z\)之间的映射关系也比较确定,因此可以同时得到编码模型和生成模型,实现隐变量编辑等需求,但是它的缺点也很明显,因为我们建模概率分布的能力有限,这3个分布都只能建模为正态分布,这限制了模型的表达能力,最终通常得偏模糊的生成结果。
为了突破这个限制,DDPM将编码过程和生成过程分解为\(T\)步:
\[\begin{equation} \begin{aligned} &编码:x=x_0 \longrightarrow x_1 \longrightarrow ... \longrightarrow x_{T-1} \longrightarrow x_T =z \\ &解码:z = x_T \longrightarrow x_{T-1} \longrightarrow...\longrightarrow x_1\longrightarrow x_0 = x \end{aligned} \end{equation} \]这样一来,每一个\(p(x_t|x_{t-1})\)和\(q(x_{t-1}|x_t)\)仅仅建模一个微小变化,他们依然建模为正态分布。
title: 同样是正态分布,为什么分解为多步会比单步要好?
collapse: true
这是因为对于微小变化来说,可以用正态分布足够近似地建模,类似于曲线在小范围内可以用直线近似,多步分解就有点像用分段线性函数拟合复杂曲线,因此理论上可以突破传统单步VAE的拟合能力限制。
联合散度
现在的计划就是通过递归式分解(2)来增强传统VAE的能力,每一步编码过程都被建模成\(p(x_t|x_{t-1})\),每一步的生成过程则被建模成\(q(x_{t-1}|x_t)\),相应的联合分布就是:
\(x_0\)代表真实样本,所以\(\tilde{ p}(x_0)\)就是数据分布;而\(x_T\)代表最终的编码,所以\(q(x_T)\)就是先验分布; 剩下的\(p(x_t|x_{t-1})\)、\(q(x_{t-1}|x_t)\)就代表着编码、生成的一小步。
在VAE中,就是最小化联合分布的\(KL\)散度,对于DDPM而言,也是如此,上面已经给出了两个联合分布,所以DDPM的目的就是最小化:
\[\begin{equation}KL(p\Vert q) = \int p(\boldsymbol{x}_T|\boldsymbol{x}_{T-1})\cdots p(\boldsymbol{x}_1|\boldsymbol{x}_0) \tilde{p}(\boldsymbol{x}_0) \log \frac{p(\boldsymbol{x}_T|\boldsymbol{x}_{T-1})\cdots p(\boldsymbol{x}_1|\boldsymbol{x}_0) \tilde{p}(\boldsymbol{x}_0)}{q(\boldsymbol{x}_0|\boldsymbol{x}_1)\cdots q(\boldsymbol{x}_{T-1}|\boldsymbol{x}_T) q(\boldsymbol{x}_T)} d\boldsymbol{x}_0 d\boldsymbol{x}_1\cdots d\boldsymbol{x}_T\end{equation} \tag{4} \]以上式子就是DDPM的优化目标,接下来就是将\(p(x_t|x_{t-1})\)、\(q(x_{t-1}|x_t)\)具体形式定下来,然后简化DDPM的优化目标。
分而治之
首先我们要知道,DDPM只是想做一个生成模型,所以它只是将每一步的编码建立为极简单的正态分布:\(p(\boldsymbol{x}_t|\boldsymbol{x}_{t-1})=\mathcal{N}(\boldsymbol{x}_t;\alpha_t \boldsymbol{x}_{t-1}, \beta_t^2 \boldsymbol{I})\) , 其主要的特点是均值向量仅仅由输入\(x_{t-1}\)乘以一个标量\(\alpha_t\)得到,相比之下传统VAE的均值方差都是用神经网络学习出来的,因此DDPM是放弃了模型的编码能力,最终得到一个纯粹的生成模型;至于\(q(x_{t-1}|x_t)\),则被建模成均值向量可学习的正态分布\(\mathcal{N}(\boldsymbol{x}_{t-1};\boldsymbol{\mu}(\boldsymbol{x}_t), \sigma_t^2 \boldsymbol{I})\)。其中\(\alpha_t,\beta_t, \sigma_t\) 都不是可训练参数,而是事先设定好的值(怎么设置之后讨论),所以整个模型拥有可训练参数的就只有\(\mu(x_t)\)
由于目前分布\(p\)中不含任何的可训练参数,因此目标(4)中关于\(p\)的积分就只是贡献一个可以忽略的常数,所以(4)等价于:
\[\begin{equation}\begin{aligned}&\,-\int p(\boldsymbol{x}_T|\boldsymbol{x}_{T-1})\cdots p(\boldsymbol{x}_1|\boldsymbol{x}_0) \tilde{p}(\boldsymbol{x}_0) \log q(\boldsymbol{x}_0|\boldsymbol{x}_1)\cdots q(\boldsymbol{x}_{T-1}|\boldsymbol{x}_T) q(\boldsymbol{x}_T) d\boldsymbol{x}_0 d\boldsymbol{x}_1\cdots d\boldsymbol{x}_T \\ =&\,-\int p(\boldsymbol{x}_T|\boldsymbol{x}_{T-1})\cdots p(\boldsymbol{x}_1|\boldsymbol{x}_0) \tilde{p}(\boldsymbol{x}_0) \left[\log q(\boldsymbol{x}_T) + \sum_{t=1}^T\log q(\boldsymbol{x}_{t-1}|\boldsymbol{x}_t)\right] d\boldsymbol{x}_0 d\boldsymbol{x}_1\cdots d\boldsymbol{x}_T \end{aligned}\end{equation} \tag{5} \]由于先验分布\(q(x_T)\)一般都是取标准正态分布,也是没有参数的,所以这一项也只是贡献一个常数。因此需要计算的就是每一项
\[\begin{equation}\begin{aligned}&\,-\int p(\boldsymbol{x}_T|\boldsymbol{x}_{T-1})\cdots p(\boldsymbol{x}_1|\boldsymbol{x}_0) \tilde{p}(\boldsymbol{x}_0) \log q(\boldsymbol{x}_{t-1}|\boldsymbol{x}_t) d\boldsymbol{x}_0 d\boldsymbol{x}_1\cdots d\boldsymbol{x}_T\\ =&\,-\int p(\boldsymbol{x}_t|\boldsymbol{x}_{t-1})\cdots p(\boldsymbol{x}_1|\boldsymbol{x}_0) \tilde{p}(\boldsymbol{x}_0) \log q(\boldsymbol{x}_{t-1}|\boldsymbol{x}_t) d\boldsymbol{x}_0 d\boldsymbol{x}_1\cdots d\boldsymbol{x}_t\\ =&\,-\int p(\boldsymbol{x}_t|\boldsymbol{x}_{t-1})p(\boldsymbol{x}_{t-1}|\boldsymbol{x}_0) \tilde{p}(\boldsymbol{x}_0) \log q(\boldsymbol{x}_{t-1}|\boldsymbol{x}_t) d\boldsymbol{x}_0 d\boldsymbol{x}_{t-1}d\boldsymbol{x}_t \end{aligned}\end{equation} \tag{6} \]其中第一个等号是因为\(q(x_{t-1}|x_t)\)至多依赖到\(x_t\),因此\(t+1\)到\(T\)的分布可以直接积分为1;第二个等号则是因为\(q(x_{t-1}|x_t)\)也不依赖于\(x_1,..,x_{t-2}\),所以关于他们的积分我们也可以事先算出,结果为\(p(\boldsymbol{x}_{t-1}|\boldsymbol{x}_0)=\mathcal{N}(\boldsymbol{x}_{t-1};\bar{\alpha}_{t-1} \boldsymbol{x}_0, \bar{\beta}_{t-1}^2 \boldsymbol{I})\),该结果可以参考下一节的式(9)
场景再现
接下来的过程就是和上一节的"又如何建"基本一致
1. 除去优化无关的常数,$-logq(x_{t-1}|x_t)$这一项所贡献的就是$\frac{1}{2\sigma_t^2}\left\Vert\boldsymbol{x}_{t-1} - \boldsymbol{\mu}(\boldsymbol{x}_t)\right\Vert^2$;
2. $p(x_{t-1}|x_0)$意味着$\boldsymbol{x}_{t-1} = \bar{\alpha}_{t-1}\boldsymbol{x}_0 + \bar{\beta}_{t-1}\bar{\boldsymbol{\varepsilon}}_{t-1}$, $p(x_t|x_{t-1})$又意味着$\boldsymbol{x}_t = \alpha_t \boldsymbol{x}_{t-1} + \beta_t \boldsymbol{\varepsilon}_t$, 其中$\bar{\epsilon}_{t-1},\epsilon_t \sim \mathcal{N}(0, I)$;
3. 由$\boldsymbol{x}_{t-1} = \frac{1}{\alpha_t}\left(\boldsymbol{x}_t - \beta_t \boldsymbol{\varepsilon}_t\right)$则启发我们将$\mu(x_t)$参数化为$\boldsymbol{\mu}(\boldsymbol{x}_t) = \frac{1}{\alpha_t}\left(\boldsymbol{x}_t - \beta_t \boldsymbol{\epsilon}_{\boldsymbol{\theta}}(\boldsymbol{x}_t, t)\right)$.
这一系列变换下来,优化目标等价于
\[\begin{equation}\frac{\beta_t^2}{\alpha_t^2\sigma_t^2}\mathbb{E}_{\bar{\boldsymbol{\varepsilon}}_{t-1},\boldsymbol{\varepsilon}_t\sim \mathcal{N}(\boldsymbol{0},\boldsymbol{I}),\boldsymbol{x}_0\sim \tilde{p}(\boldsymbol{x}_0)}\left[\left\Vert \boldsymbol{\varepsilon}_t - \boldsymbol{\epsilon}_{\boldsymbol{\theta}}(\bar{\alpha}_t\boldsymbol{x}_0 + \alpha_t\bar{\beta}_{t-1}\bar{\boldsymbol{\varepsilon}}_{t-1} + \beta_t \boldsymbol{\varepsilon}_t, t)\right\Vert^2\right]\end{equation} \tag{7} \]随后按照"降低方差"一节做换元,结果为:
\[\begin{equation}\frac{\beta_t^4}{\bar{\beta}_t^2\alpha_t^2\sigma_t^2}\mathbb{E}_{\boldsymbol{\varepsilon}\sim \mathcal{N}(\boldsymbol{0},\boldsymbol{I}),\boldsymbol{x}_0\sim \tilde{p}(\boldsymbol{x}_0)}\left[\left\Vert\boldsymbol{\varepsilon} - \frac{\bar{\beta}_t}{\beta_t}\boldsymbol{\epsilon}_{\boldsymbol{\theta}}(\bar{\alpha}_t\boldsymbol{x}_0 + \bar{\beta}_t\boldsymbol{\varepsilon}, t)\right\Vert^2\right]\end{equation} \tag{8} \]这就得到了DDPM的训练目标了(原论文通过实验发现,去掉上式前面的系数后实际效果更好些)。它是我们从VAE的优化目标出发,逐步简化积分结果得到的,虽然有点长,但每一步都是有章可循的,有计算难度,但没有思路上的难度。
超参设置
title: 讨论$\alpha_t,\beta_t,\sigma_t$的选择问题?
对于\(p(x_t|x_{t-1})\)来说,习惯上约定\(\alpha_t^2 + \beta_t^2=1\) ,这样就减少了一般的参数,并且有助于简化形式,由于正态分布的叠加性,在此约束下我们有
\[\begin{equation}p(\boldsymbol{x}_t|\boldsymbol{x}_0) = \int p(\boldsymbol{x}_t|\boldsymbol{x}_{t-1})\cdots p(\boldsymbol{x}_1|\boldsymbol{x}_0) d\boldsymbol{x}_1\cdots d\boldsymbol{x}_{t-1} = \mathcal{N}(\boldsymbol{x}_t;\bar{\alpha}_t \boldsymbol{x}_0, \bar{\beta}_t^2 \boldsymbol{I})\end{equation} \tag{9} \]其中\(\bar{\alpha}_t = \alpha_1\cdots\alpha_t\) 而\(\bar{\beta}_t = \sqrt{1-\bar{\alpha}_t^2}\), 这样一来\(p(x_t|x_0)\)就具有比较简约的形式。是怎么想到\(\alpha_t^2 + \beta_t^2=1\)这个约束呢?我们知道\(\mathcal{N}(\boldsymbol{x}_t;\alpha_t \boldsymbol{x}_{t-1}, \beta_t^2 \boldsymbol{I})\)意味着\(\boldsymbol{x}_t = \alpha_t \boldsymbol{x}_{t-1} + \beta_t \boldsymbol{\varepsilon}_t,\boldsymbol{\varepsilon}_t\sim \mathcal{N}(\boldsymbol{0},\boldsymbol{I})\),如果\(x_{t-1}\)也是\(\sim \mathcal{N}(\boldsymbol{0},\boldsymbol{I})\)的话,我们就希望\(x_t\)也是\(\sim \mathcal{N}(\boldsymbol{0},\boldsymbol{I})\),所以就确定了\(\alpha_t^2+\beta_t^2=1\)了。
前面说了,\(q(x_T)\)一般都取标准正太分布\(\mathcal{N}(\boldsymbol{x}_T;\boldsymbol{0}, \boldsymbol{I})\)。而我们学习目标是最小化两个联合分布的KL散度,即希望\(p=q\),那么他们的边缘分布自然也相等,所以我们希望
\[\begin{equation}q(\boldsymbol{x}_T) = \int p(\boldsymbol{x}_T|\boldsymbol{x}_{T-1})\cdots p(\boldsymbol{x}_1|\boldsymbol{x}_0) \tilde{p}(\boldsymbol{x}_0) d\boldsymbol{x}_0 d\boldsymbol{x}_1\cdots d\boldsymbol{x}_{T-1} = \int p(\boldsymbol{x}_T|\boldsymbol{x}_0) \tilde{p}(\boldsymbol{x}_0) d\boldsymbol{x}_0 \end{equation} \tag{10} \]由于数据分布\(\tilde{p}(\boldsymbol{x}_0)\)是任意的,所以要使上式恒成立,只能让\(p(\boldsymbol{x}_T|\boldsymbol{x}_0)=q(\boldsymbol{x}_T)\),即退化为与\(x_0\)无关的标准正态分布,这意味着我们需要设计适当的\(\alpha_t\), 使得\(\bar{\alpha}_T\approx 0\)。同时这再次告诉我们,DDPM是没有编码能力的,最终的\(p(\boldsymbol{x}_T|\boldsymbol{x}_0)\)可以说跟输入\(x_0\)无关。
至于\(\sigma_t\),理论上不同的数据分布\(\tilde{p}(\boldsymbol{x}_0)\) 对应不同的最优\(\sigma_t\), 但是我们又不想将\(\sigma_t\)设为可训练参数,所以只好选择一些特殊的\(\tilde{p}(\boldsymbol{x}_0)\)来推导相应的最优\(\sigma_t\),并认为由特例推导出来的的\(\sigma_t\)可以泛化到一般的数据分布。两个简单的例子:
title: 例子
collapse: true
1. 假设训练集只有一个样本$x_*$,即$\tilde{p}(\boldsymbol{x}_0)$是狄拉克分布$\delta(\boldsymbol{x}_0 - \boldsymbol{x}_*)$,可以推出最优的$\sigma_t = \frac{\bar{\beta}_{t-1}}{\bar{\beta}_t}\beta_t$
2. 假设数据分布$\tilde{p}(\boldsymbol{x}_0)$服从标准正态分布,这时候可以推出最优的$\sigma_t = \beta_t$。
推导过程 2.3节 <b style="color: #219ebc">遗留问题</b>
2.3 DDPM=贝叶斯+去噪
原文链接:生成扩散模型漫谈(三):DDPM = 贝叶斯 + 去噪
2.1节用通俗类比的方式推导,2.2节用变分自编码器的方法进行推导。两种方案各有特点,前者更为直白易懂,但无法做更多的理论延伸和定理理解,后者理论分析上更加完备一些,但稍显形式化,启发性不足。
这一部分用贝叶斯来简化计算,整个过程的推敲味道更浓,很有启发性。不仅如此,这种推理方式与DDIM有着紧密的联系。
回顾
DDPM的建模流程:
正向就是将样本数据\(x\)逐渐变为随机噪声\(z\)的过程,反向就是将随机噪声\(z\)逐渐变为样本数据\(x\)的过程,反向过程就是我们希望的“生成模型”。
正向过程,每一步表示为:
或者写成\(p(\boldsymbol{x}_t|\boldsymbol{x}_{t-1})=\mathcal{N}(\boldsymbol{x}_t;\alpha_t \boldsymbol{x}_{t-1},\beta_t^2 \boldsymbol{I})\)。在约束\(\alpha_t^2+\beta_t^2=1\)之下,我们有:
\[\begin{equation}\begin{aligned} \boldsymbol{x}_t =&\, \alpha_t \boldsymbol{x}_{t-1} + \beta_t \boldsymbol{\varepsilon}_t \\ =&\, \alpha_t \big(\alpha_{t-1} \boldsymbol{x}_{t-2} + \beta_{t-1} \boldsymbol{\varepsilon}_{t-1}\big) + \beta_t \boldsymbol{\varepsilon}_t \\ =&\,\cdots\\ =&\,(\alpha_t\cdots\alpha_1) \boldsymbol{x}_0 + \underbrace{(\alpha_t\cdots\alpha_2)\beta_1 \boldsymbol{\varepsilon}_1 + (\alpha_t\cdots\alpha_3)\beta_2 \boldsymbol{\varepsilon}_2 + \cdots + \alpha_t\beta_{t-1} \boldsymbol{\varepsilon}_{t-1} + \beta_t \boldsymbol{\varepsilon}_t}_{\sim \mathcal{N}(\boldsymbol{0}, (1-\alpha_t^2\cdots\alpha_1^2)\boldsymbol{I})} \end{aligned}\end{equation} \tag{3} \]从而可以求出\(p(\boldsymbol{x}_t|\boldsymbol{x}_0)=\mathcal{N}(\boldsymbol{x}_t;\bar{\alpha}_t \boldsymbol{x}_0,\bar{\beta}_t^2 \boldsymbol{I})\),其中\(\bar{\alpha}_t = \alpha_1\cdots\alpha_t\),而\(\bar{\beta}_t = \sqrt{1-\bar{\alpha}_t^2}\)
DDPM要做的事情,就是从上述信息中求出反向过程中所需要的\(p(x_{t-1}|x_t)\),这样我们就能实现从任意一个\(x_T=z\)出发,逐步采样出\(\boldsymbol{x}_{T-1},\boldsymbol{x}_{T-2},\cdots,\boldsymbol{x}_1\),最后得到随机生成的样本数据\(x_0=x\)。
贝叶斯推导
根据贝叶斯定理,我们可以得到:
然而,我们并不知道\(p(x_{t-1}),p(x_t)\)的表达式,所以此路不通。但是我们可以退而求其次,在给定\(x_0\)的条件下使用贝叶斯定理:
\[\begin{equation}p(\boldsymbol{x}_{t-1}|\boldsymbol{x}_t, \boldsymbol{x}_0) = \frac{p(\boldsymbol{x}_t|\boldsymbol{x}_{t-1})p(\boldsymbol{x}_{t-1}|\boldsymbol{x}_0)}{p(\boldsymbol{x}_t|\boldsymbol{x}_0)}\end{equation} \tag{5} \]这样修改自然是因为\(p(\boldsymbol{x}_t|\boldsymbol{x}_{t-1}),p(\boldsymbol{x}_{t-1}|\boldsymbol{x}_0),p(\boldsymbol{x}_t|\boldsymbol{x}_0)\)都是已知的,所以上式是可计算的,代入各自的表达式得到:
\[\begin{equation}p(\boldsymbol{x}_{t-1}|\boldsymbol{x}_t, \boldsymbol{x}_0) = \mathcal{N}\left(\boldsymbol{x}_{t-1};\frac{\alpha_t\bar{\beta}_{t-1}^2}{\bar{\beta}_t^2}\boldsymbol{x}_t + \frac{\bar{\alpha}_{t-1}\beta_t^2}{\bar{\beta}_t^2}\boldsymbol{x}_0,\frac{\bar{\beta}_{t-1}^2\beta_t^2}{\bar{\beta}_t^2} \boldsymbol{I}\right)\end{equation} \tag{6} \]

Fig. 推导-技巧
去噪过程
我们现在得到了\(p(x_{t-1}|x_t,x_0)\),它有显式的解,但并非我们想要的最终答案,因为我们只想通过\(x_t\),而不能依赖\(x_0\),\(x_0\)是我们最终想要生成的结果。接下来,一个异想天开的想法是:
title: 如果我们能够通过$x_t$来预测$x_0$,那么不就可以消去$p(x_{t-1}|x_t,x_0)$中的$x_0$,使得它只依赖于$x_t$了吗?
说干就干,我们就用\(\bar{\mu}(x_t)\)来预估\(x_0\),损失函数为\(\Vert \boldsymbol{x}_0 - \bar{\boldsymbol{\mu}}(\boldsymbol{x}_t)\Vert^2\)。训练完成后,我们就认为
\[\begin{equation}p(\boldsymbol{x}_{t-1}|\boldsymbol{x}_t) \approx p(\boldsymbol{x}_{t-1}|\boldsymbol{x}_t, \boldsymbol{x}_0=\bar{\boldsymbol{\mu}}(\boldsymbol{x}_t)) = \mathcal{N}\left(\boldsymbol{x}_{t-1}; \frac{\alpha_t\bar{\beta}_{t-1}^2}{\bar{\beta}_t^2}\boldsymbol{x}_t + \frac{\bar{\alpha}_{t-1}\beta_t^2}{\bar{\beta}_t^2}\bar{\boldsymbol{\mu}}(\boldsymbol{x}_t),\frac{\bar{\beta}_{t-1}^2\beta_t^2}{\bar{\beta}_t^2} \boldsymbol{I}\right)\end{equation} \tag{10} \]在\(\Vert \boldsymbol{x}_0 - \bar{\boldsymbol{\mu}}(\boldsymbol{x}_t)\Vert^2\)中,\(x_0\)代表原始数据,\(x_t\)代表带噪数据,所以这实际上在训练一个去噪模型,这也就是DDPM的第一个"D"的含义(Denoising)
具体来说,\(p(\boldsymbol{x}_t|\boldsymbol{x}_0)=\mathcal{N}(\boldsymbol{x}_t;\bar{\alpha}_t \boldsymbol{x}_0,\bar{\beta}_t^2 \boldsymbol{I})\)意味着\(\boldsymbol{x}_t = \bar{\alpha}_t \boldsymbol{x}_0 + \bar{\beta}_t \boldsymbol{\varepsilon},\boldsymbol{\varepsilon}\sim\mathcal{N}(\boldsymbol{0}, \boldsymbol{I})\),或者写成\(\boldsymbol{x}_0 = \frac{1}{\bar{\alpha}_t}\left(\boldsymbol{x}_t - \bar{\beta}_t \boldsymbol{\varepsilon}\right)\),这启发我们将\(\bar{\mu}(x_t)\)参数化为:
\[\begin{equation}\bar{\boldsymbol{\mu}}(\boldsymbol{x}_t) = \frac{1}{\bar{\alpha}_t}\left(\boldsymbol{x}_t - \bar{\beta}_t \boldsymbol{\epsilon}_{\boldsymbol{\theta}}(\boldsymbol{x}_t, t)\right)\end{equation} \tag{11} \]此时损失函数为:
\[\begin{equation}\Vert \boldsymbol{x}_0 - \bar{\boldsymbol{\mu}}(\boldsymbol{x}_t)\Vert^2 = \frac{\bar{\beta}_t^2}{\bar{\alpha}_t^2}\left\Vert\boldsymbol{\varepsilon} - \boldsymbol{\epsilon}_{\boldsymbol{\theta}}(\bar{\alpha}_t \boldsymbol{x}_0 + \bar{\beta}_t \boldsymbol{\varepsilon}, t)\right\Vert^2\end{equation} \tag{12} \]省去前面的系数,就得到DDPM原论文所用到的损失函数了。可以发现,本文是直接得出了从\(x_t\)到\(x_0\)去噪过程,而不是像之前两篇文章那样,通过\(x_t\)到\(x_{t-1}\)的去噪过程再加上积分变换来推导,相比之下本文的推导更加一步到位了。
另一边,我们将式(11)代入(10)中,化简得到
\[\begin{equation} p(\boldsymbol{x}_{t-1}|\boldsymbol{x}_t) \approx p(\boldsymbol{x}_{t-1}|\boldsymbol{x}_t, \boldsymbol{x}_0=\bar{\boldsymbol{\mu}}(\boldsymbol{x}_t)) = \mathcal{N}\left(\boldsymbol{x}_{t-1}; \frac{1}{\alpha_t}\left(\boldsymbol{x}_t - \frac{\beta_t^2}{\bar{\beta}_t}\boldsymbol{\epsilon}_{\boldsymbol{\theta}}(\boldsymbol{x}_t, t)\right),\frac{\bar{\beta}_{t-1}^2\beta_t^2}{\bar{\beta}_t^2} \boldsymbol{I}\right)\end{equation} \tag{13} \]这就是反向的采样过程所用的分布,连同采样过程所用的方差也是一并确定下来的。至此,DDPM推导完毕
title:推导: 将(11)代入到(10)的主要化简难度就是计算
$\begin{equation}\begin{aligned}\frac{\alpha_t\bar{\beta}_{t-1}^2}{\bar{\beta}_t^2} + \frac{\bar{\alpha}_{t-1}\beta_t^2}{\bar{\alpha}_t\bar{\beta}_t^2} =&\, \frac{\alpha_t\bar{\beta}_{t-1}^2 + \beta_t^2/\alpha_t}{\bar{\beta}_t^2} = \frac{\alpha_t^2(1-\bar{\alpha}_{t-1}^2) + \beta_t^2}{\alpha_t\bar{\beta}_t^2} = \frac{1-\bar{\alpha}_t^2}{\alpha_t\bar{\beta}_t^2} = \frac{1}{\alpha_t}
\end{aligned}\end{equation}$
预估修正
有一个有趣的地方:我们要做的事情,就是想将\(x_T\)慢慢变为\(x_0\),我们在借用\(p(x_{t-1}|x_t,x_0)\) 近似\(p(x_{t-1}|x_t)\)时,却包含了用"\(\bar{\mu}(x_t)\)来预估\(x_0\)"这一步,这要是能预估准的话,那就直接一步到位了,还需要逐步采样吗?
真实情况是,“用\(\bar{\mu}(x_t)\)来预估\(x_0\)”当然不会太准的,至少开始的相当多步内不会太准。它仅仅起到了一个前瞻性的预估作用,然后我们只用\(p(x_{t-1}|x_t)\)来推进一小步,这就是很多数值算法中的“预估-修正”思想,即我们用一个粗糙的解往前推很多步,然后利用这个粗糙的结果将最终结果推进一小步,以此来逐步获得更为精细的解。
遗留问题
最后,在使用贝叶斯定理一节中,说(4)没发直接用的原因是\(p(x_{t-1})\)和\(p(x_t)\)均不知道。因为根据定义,我们有:
其中\(p(x_t|x_0)\)是知道的,而数据分布\(\tilde{p}(\boldsymbol{x}_0)\)无法提前预知,所以不能进行计算。不过有两个特殊的例子,是可以直接将两者算出来的,这里进行补充,其结果也正好是上一篇文章遗留的方差选取问题的答案。
第一个例子是整个数据集只有一个样本,不失一般性,假设该样本为\(0\),此时\(\tilde{p}(\boldsymbol{x}_0)\)为狄拉克分布\(\delta(\boldsymbol{x}_0)\),可以直接算出\(p(\boldsymbol{x}_t)=p(\boldsymbol{x}_t|\boldsymbol{0})\)。继而代入(4),可以发现结果正好是\(p(x_{t-1}|x_t,x_0)\)取\(x_0=0\)的特例,即
\[\begin{equation}p(\boldsymbol{x}_{t-1}|\boldsymbol{x}_t) = p(\boldsymbol{x}_{t-1}|\boldsymbol{x}_t, \boldsymbol{x}_0=\boldsymbol{0}) = \mathcal{N}\left(\boldsymbol{x}_{t-1};\frac{\alpha_t\bar{\beta}_{t-1}^2}{\bar{\beta}_t^2}\boldsymbol{x}_t,\frac{\bar{\beta}_{t-1}^2\beta_t^2}{\bar{\beta}_t^2} \boldsymbol{I}\right)\end{equation} \tag{16} \]我们主要关心其方差为\(\frac{\bar{\beta}_{t-1}^2\beta_t^2}{\bar{\beta}_t^2}\),这便是采样方差的选择之一。
第二个例子是数据集服从标准正态分布,即\(\tilde{p}(\boldsymbol{x}_0)=\mathcal{N}(\boldsymbol{x}_0;\boldsymbol{0},\boldsymbol{I})\)。前面我们说了\(p(\boldsymbol{x}_t|\boldsymbol{x}_0)=\mathcal{N}(\boldsymbol{x}_t;\bar{\alpha}_t \boldsymbol{x}_0,\bar{\beta}_t^2 \boldsymbol{I})\)意味着\(\boldsymbol{x}_t = \bar{\alpha}_t \boldsymbol{x}_0 + \bar{\beta}_t \boldsymbol{\varepsilon},\boldsymbol{\varepsilon}\sim\mathcal{N}(\boldsymbol{0}, \boldsymbol{I})\),而此时根据假设还有\(x_0\sim \mathcal{N}(0,I)\),由于正态分布的叠加性,\(x_t\)正好也服从标准正态分布。将标准正态分布的概率密度代入(4)后,结果的指数部分除掉\(-1/2\)因子外,结果是:
\[\begin{equation}\frac{\Vert \boldsymbol{x}_t - \alpha_t \boldsymbol{x}_{t-1}\Vert^2}{\beta_t^2} + \Vert \boldsymbol{x}_{t-1}\Vert^2 - \Vert \boldsymbol{x}_t\Vert^2\end{equation} \tag{17} \]跟推导\(p(x_{t-1}|x_t,x_0)\)的过程类似,可以得到上述指数对应于
\[\begin{equation}p(\boldsymbol{x}_{t-1}|\boldsymbol{x}_t) = \mathcal{N}\left(\boldsymbol{x}_{t-1};\alpha_t\boldsymbol{x}_t,\beta_t^2 \boldsymbol{I}\right)\end{equation} \tag{18} \]我们同样主要关心其方差为\(\beta_t^2\),这便是采样方差的另一个选择。
3. DDIM=高观点DDPM
前面三篇文章从不同视角去解读了DDPM,那么它是否存在一个更高的理解视角?答案:DDIM
3.1 思路分析
在2.3节中,从贝叶斯角度推导DDPM,推导路线可以简单归纳如下:
\[\begin{equation}p(\boldsymbol{x}_t|\boldsymbol{x}_{t-1})\xrightarrow{\text{推导}}p(\boldsymbol{x}_t|\boldsymbol{x}_0)\xrightarrow{\text{推导}}p(\boldsymbol{x}_{t-1}|\boldsymbol{x}_t, \boldsymbol{x}_0)\xrightarrow{\text{近似}}p(\boldsymbol{x}_{t-1}|\boldsymbol{x}_t)\end{equation} \tag{1} \]这个过程是一步步递进的。然而,我们发现最终结果有着两个特点:
1. 损失函数只依赖$p(x_t|x_0)$
2. 采样过程只依赖于$p(x_{t-1}|x_t)$
也就是说,尽管整个过程是以\(p(x_t|x_{t-1})\)为出发点一步步往前推的,但是从结果上来看,压根就没有\(p(x_t|x_{t-1})\)的事。那么,我们大胆地"异想天开":
title: 高观点1.:既然结果跟$p(x_t|x_{t-1})$无关,可不可以干脆"过河拆桥",将$p(x_t|x_{t-1})$从整个过程中去掉?
DDIM正是这个产物。
3.2 待定系数
根据2.3的贝叶斯推导:
\[\begin{equation}p(\boldsymbol{x}_{t-1}|\boldsymbol{x}_t, \boldsymbol{x}_0) = \frac{p(\boldsymbol{x}_t|\boldsymbol{x}_{t-1})p(\boldsymbol{x}_{t-1}|\boldsymbol{x}_0)}{p(\boldsymbol{x}_t|\boldsymbol{x}_0)}\end{equation} \tag{2} \]没有给定\(p(x_t|x_{t-1})\)怎么能得到\(p(\boldsymbol{x}_{t-1}|\boldsymbol{x}_t, \boldsymbol{x}_0)\)? 理论上在没有给定\(p(x_t|x_{t-1})\)的情况下,\(p(\boldsymbol{x}_{t-1}|\boldsymbol{x}_t, \boldsymbol{x}_0)\)的解空间更大,某种意义来说更加容易推导,此时它只需要满足边际分布条件:
\[\begin{equation}\int p(\boldsymbol{x}_{t-1}|\boldsymbol{x}_t, \boldsymbol{x}_0) p(\boldsymbol{x}_t|\boldsymbol{x}_0) d\boldsymbol{x}_t = p(\boldsymbol{x}_{t-1}|\boldsymbol{x}_0)\end{equation} \tag{3} \]我们用待定系数法来求解这个方程,在2.3中,所解出的\(p(\boldsymbol{x}_{t-1}|\boldsymbol{x}_t, \boldsymbol{x}_0)\)是一个正态分布,所以我们可以更一般的设:
\[\begin{equation}p(\boldsymbol{x}_{t-1}|\boldsymbol{x}_t, \boldsymbol{x}_0) = \mathcal{N}(\boldsymbol{x}_{t-1}; \kappa_t \boldsymbol{x}_t + \lambda_t \boldsymbol{x}_0, \sigma_t^2 \boldsymbol{I})\end{equation} \tag{4} \]其中\(\kappa_t,\lambda_t,\sigma_t\)都是待定系数,而为了不重新训练模型,我们不改变\(p(x_{t-1}|x_0)\)和\(p(x_t|x_0)\),于是我们可以列出
\[\begin{array}{c|c|c} \hline \text{记号} & \text{含义} & \text{采样}\\ \hline p(\boldsymbol{x}_{t-1}|\boldsymbol{x}_0) & \mathcal{N}(\boldsymbol{x}_{t-1};\bar{\alpha}_{t-1} \boldsymbol{x}_0,\bar{\beta}_{t-1}^2 \boldsymbol{I}) & \boldsymbol{x}_{t-1} = \bar{\alpha}_{t-1} \boldsymbol{x}_0 + \bar{\beta}_{t-1} \boldsymbol{\varepsilon} \\ \hline p(\boldsymbol{x}_t|\boldsymbol{x}_0) & \mathcal{N}(\boldsymbol{x}_t;\bar{\alpha}_t \boldsymbol{x}_0,\bar{\beta}_t^2 \boldsymbol{I}) & \boldsymbol{x}_t = \bar{\alpha}_t \boldsymbol{x}_0 + \bar{\beta}_t \boldsymbol{\varepsilon}_1 \\ \hline p(\boldsymbol{x}_{t-1}|\boldsymbol{x}_t, \boldsymbol{x}_0) & \mathcal{N}(\boldsymbol{x}_{t-1}; \kappa_t \boldsymbol{x}_t + \lambda_t \boldsymbol{x}_0, \sigma_t^2 \boldsymbol{I}) & \boldsymbol{x}_{t-1} = \kappa_t \boldsymbol{x}_t + \lambda_t \boldsymbol{x}_0 + \sigma_t \boldsymbol{\varepsilon}_2 \\ \hline {\begin{array}{c}\int p(\boldsymbol{x}_{t-1}|\boldsymbol{x}_t, \boldsymbol{x}_0) \\ p(\boldsymbol{x}_t|\boldsymbol{x}_0) d\boldsymbol{x}_t\end{array}} & & {\begin{aligned}\boldsymbol{x}_{t-1} =&\, \kappa_t \boldsymbol{x}_t + \lambda_t \boldsymbol{x}_0 + \sigma_t \boldsymbol{\varepsilon}_2 \\ =&\, \kappa_t (\bar{\alpha}_t \boldsymbol{x}_0 + \bar{\beta}_t \boldsymbol{\varepsilon}_1) + \lambda_t \boldsymbol{x}_0 + \sigma_t \boldsymbol{\varepsilon}_2 \\ =&\, (\kappa_t \bar{\alpha}_t + \lambda_t) \boldsymbol{x}_0 + (\kappa_t\bar{\beta}_t \boldsymbol{\varepsilon}_1 + \sigma_t \boldsymbol{\varepsilon}_2) \\ \end{aligned}} \\ \hline \end{array} \]其中\(\boldsymbol{\varepsilon},\boldsymbol{\varepsilon}_1,\boldsymbol{\varepsilon}_2\sim \mathcal{N}(\boldsymbol{0},\boldsymbol{I})\),并且由于正态分布的叠加性我们知道\(\kappa_t\bar{\beta}_t \boldsymbol{\varepsilon}_1 + \sigma_t \boldsymbol{\varepsilon}_2\sim \sqrt{\kappa_t^2\bar{\beta}_t^2 + \sigma_t^2} \boldsymbol{\varepsilon}\)。对比\(x_{t-1}\)的两个采样形式,我们发现要(3)成立,只需要满足两个方程
\[\begin{equation}\bar{\alpha}_{t-1} = \kappa_t \bar{\alpha}_t + \lambda_t, \qquad\bar{\beta}_{t-1} = \sqrt{\kappa_t^2\bar{\beta}_t^2 + \sigma_t^2}\end{equation} \tag{5} \]可以看到有3个未知数,但只有两个方程,这就是为什么说没有给定\(p(x_t|x_{t-1})\)时,解空间反而更加大了。将\(\sigma_t\)视为可变参数,可以解出
\[\begin{equation}\kappa_t = \frac{\sqrt{\bar{\beta}_{t-1}^2 - \sigma_t^2}}{\bar{\beta}_t},\qquad \lambda_t = \bar{\alpha}_{t-1} - \frac{\bar{\alpha}_t\sqrt{\bar{\beta}_{t-1}^2 - \sigma_t^2}}{\bar{\beta}_t}\end{equation} \tag{6} \]或者写成
\[\begin{equation}p(\boldsymbol{x}_{t-1}|\boldsymbol{x}_t, \boldsymbol{x}_0) = \mathcal{N}\left(\boldsymbol{x}_{t-1}; \frac{\sqrt{\bar{\beta}_{t-1}^2 - \sigma_t^2}}{\bar{\beta}_t} \boldsymbol{x}_t + \left(\bar{\alpha}_{t-1} - \frac{\bar{\alpha}_t\sqrt{\bar{\beta}_{t-1}^2 - \sigma_t^2}}{\bar{\beta}_t}\right) \boldsymbol{x}_0, \sigma_t^2 \boldsymbol{I}\right)\end{equation} \tag{7} \]方便起见,我们约定\(\bar{\alpha}_0=1, \bar{\beta}_0=0\)。特别地,这个结果并不需要限定\(\bar{\alpha}_t^2 + \bar{\beta}_t^2 = 1\),不过为了简化参数设置,同时也是为了跟以往的结果对齐,这里还是约定\(\bar{\alpha}_t^2 + \bar{\beta}_t^2 = 1\)
3.3 一如既往
现在我们在给定\(p(x_t|x_0)\)、\(p(x_{t-1}|x_0)\)的情况下,通过待定系数法求解了\(p(\boldsymbol{x}_{t-1}|\boldsymbol{x}_t, \boldsymbol{x}_0)\)一簇解,它带有一个自由参数\(\sigma_t\) 。用拆楼-建楼的类比来说,就是我们知道楼会被拆成什么样\(p(x_t|x_0)\)、\(p(x_{t-1}|x_0)\), 但是不知道每一步是怎么拆的【\(p(x_t|x_{t-1})\)】,然后希望从中学会每一步怎么建【\(p(x_t|x_{t-1})\)】 。当然,如果我们想看看每一步怎么拆的话,也可以反过来用贝叶斯公式
\[\begin{equation} p(\boldsymbol{x}_t|\boldsymbol{x}_{t-1}, \boldsymbol{x}_0) = \frac{p(\boldsymbol{x}_{t-1}|\boldsymbol{x}_t, \boldsymbol{x}_0) p(\boldsymbol{x}_t|\boldsymbol{x}_0)}{p(\boldsymbol{x}_{t-1}|\boldsymbol{x}_0)}\end{equation} \tag{8} \]接下来的事情,就和2.3节一模一样了:我们最终想要的\(p(x_{t-1}|x_t)\)而不是\(p(x_{t-1}|x_t,x_0)\) ,所以我们希望用
\[\begin{equation}\bar{\boldsymbol{\mu}}(\boldsymbol{x}_t) = \frac{1}{\bar{\alpha}_t}\left(\boldsymbol{x}_t - \bar{\beta}_t \boldsymbol{\epsilon}_{\boldsymbol{\theta}}(\boldsymbol{x}_t, t)\right)\end{equation} \tag{10} \]来估计\(x_0\),由于没有改动\(p(x_t|x_0)\),所以训练所用的目标函数依然是\(\left\Vert\boldsymbol{\varepsilon} - \boldsymbol{\epsilon}_{\boldsymbol{\theta}}(\bar{\alpha}_t \boldsymbol{x}_0 + \bar{\beta}_t \boldsymbol{\varepsilon}, t)\right\Vert^2\)(除掉权重系数),也就是说训练过程没有改变,我们可以用回DDPM训练好的模型,而用\(\bar{\mu}(x_t)\)替换掉(7)中的\(x_0\)后,得到
\[\begin{equation}\begin{aligned} p(\boldsymbol{x}_{t-1}|\boldsymbol{x}_t) \approx&\, p(\boldsymbol{x}_{t-1}|\boldsymbol{x}_t, \boldsymbol{x}_0=\bar{\boldsymbol{\mu}}(\boldsymbol{x}_t)) \\ =&\, \mathcal{N}\left(\boldsymbol{x}_{t-1}; \frac{1}{\alpha_t}\left(\boldsymbol{x}_t - \left(\bar{\beta}_t - \alpha_t\sqrt{\bar{\beta}_{t-1}^2 - \sigma_t^2}\right) \boldsymbol{\epsilon}_{\boldsymbol{\theta}}(\boldsymbol{x}_t, t)\right), \sigma_t^2 \boldsymbol{I}\right) \end{aligned}\end{equation} \tag{10} \]这就求出了生成过程所需要的\(p(\boldsymbol{x}_{t-1}|\boldsymbol{x}_t)\),其中\(\alpha_t=\frac{\bar{\alpha}_t}{\bar{\alpha}_{t-1}}\)。它的特点是训练过程没有变化(也就是说最终保存下来的模型没有变化),但生成过程却有一个可变动的参数\(\sigma_t\),就是这个参数给DDPM带来了新鲜的结果。
3.4 几个例子
原则上来说,我们对σtσt没有过多的约束,但是不同σtσt的采样过程会呈现出不同的特点,我们举几个例子进行分析。
第一个简单例子就是取\(\sigma_t = \frac{\bar{\beta}_{t-1}\beta_t}{\bar{\beta}_t}\),其中\(\beta_t = \sqrt{1 - \alpha_t^2}\),相应地有
\[\begin{equation} p(\boldsymbol{x}_{t-1}|\boldsymbol{x}_t) \approx p(\boldsymbol{x}_{t-1}|\boldsymbol{x}_t, \boldsymbol{x}_0=\bar{\boldsymbol{\mu}}(\boldsymbol{x}_t)) = \mathcal{N}\left(\boldsymbol{x}_{t-1}; \frac{1}{\alpha_t}\left(\boldsymbol{x}_t - \frac{\beta_t^2}{\bar{\beta}_t}\boldsymbol{\epsilon}_{\boldsymbol{\theta}}(\boldsymbol{x}_t, t)\right),\frac{\bar{\beta}_{t-1}^2\beta_t^2}{\bar{\beta}_t^2} \boldsymbol{I}\right)\end{equation} \tag{11} \]这就是上一篇文章所推导的DDPM。特别是,DDIM论文中还对\(\sigma_t = \eta\frac{\bar{\beta}_{t-1}\beta_t}{\bar{\beta}_t}\)做了对比实验,其中\(\eta\in[0, 1]\)。
第二个例子就是取\(\sigma_t=\beta_t\),这也是前两篇文章所指出的\(\sigma_t\)的两个选择之一,在此选择下式(10)未能做进一步的化简,但DDIM的实验结果显示此选择在DDPM的标准参数设置下表现还是很好的。
最特殊的一个例子是取\(\sigma=0\),此时从\(x_t\)到\(x_{t-1}\)是一个确定性变换
\[\begin{equation}\boldsymbol{x}_{t-1} = \frac{1}{\alpha_t}\left(\boldsymbol{x}_t - \left(\bar{\beta}_t - \alpha_t \bar{\beta}_{t-1}\right) \boldsymbol{\epsilon}_{\boldsymbol{\theta}}(\boldsymbol{x}_t, t)\right)\end{equation} \tag{12} \]这也是DDIM论文中特别关心的一个例子,准确来说,原论文的DDIM就是特指\(\sigma=0\)的情形,其中“I”的含义就是“Implicit”,意思这是一个隐式的概率模型,因为跟其他选择所不同的是,此时从给定的\(x_T=z\)出发,得到的生成结果\(x_0\)是不带随机性的。后面我们将会看到,这在理论上和实用上都带来了一些好处。
3.5 加速生成
值得注意的是,我们没有以\(p(x_t|x_{t-1})\)为出发点,所以前面的所有结果实际上全都是以\(\bar{\alpha}_t,\bar{\beta}_t\)相关记号给出的,而\(\bar{\alpha}_t,\bar{\beta}_t\)则是通过\(\alpha_t=\frac{\bar{\alpha}_t}{\bar{\alpha}_{t-1}}\)和\(\beta_t = \sqrt{1 - \alpha_t^2}\) 派生出来的记号。从损失函数\(\left\Vert\boldsymbol{\varepsilon} - \boldsymbol{\epsilon}_{\boldsymbol{\theta}}(\bar{\alpha}_t \boldsymbol{x}_0 + \bar{\beta}_t \boldsymbol{\varepsilon}, t)\right\Vert^2\)可以看出,给定了各个\(\bar{\alpha}_t\),训练过程也就确定了。
重这个过程中,DDIM进一步留意到了如下事实:
title: 高观点2:DDPM的训练结果实质上包含了塔的任意子序列参数的训练效果。
具体来说,设\(\boldsymbol{\tau} = [\tau_1,\tau_2,\dots,\tau_{\dim(\boldsymbol{\tau})}]\)是\([1,2,\cdots,T]\)的任意子序列,那么我们以\(\bar{\alpha}_{\tau_1},\bar{\alpha}_{\tau_2},\cdots,\bar{\alpha}_{\dim(\boldsymbol{\tau})}\)为参数训练一个扩散步数为\(\dim(\boldsymbol{\tau})\)步的DDPM,其目标函数实际上是原来以\(\bar{\alpha}_1,\bar{\alpha}_2,\cdots,\bar{\alpha}_T\)的\(T\)步DDPM的目标函数的一个子集!所以在模型拟合能力足够好的情况下,它其实包含了任意子序列参数的训练结果。
那么反过来想,如果有一个训练好的\(T\)步DDPM模型,我们也可以将它当成是以\(\bar{\alpha}_{\tau_1},\bar{\alpha}_{\tau_2},\cdots,\bar{\alpha}_{\dim(\boldsymbol{\tau})}\)为参数训练出来的\(\dim(\boldsymbol{\tau})\)步模型,而既然是\(\dim(\boldsymbol{\tau})\)步的模型,生成过程也就只需要\(\dim(\boldsymbol{\tau})\)步了,根据式(10)有:
\[\begin{equation}p(\boldsymbol{x}_{\tau_{i-1}}|\boldsymbol{x}_{\tau_i}) \approx \mathcal{N}\left(\boldsymbol{x}_{\tau_{i-1}}; \frac{\bar{\alpha}_{\tau_{i-1}}}{\bar{\alpha}_{\tau_i}}\left(\boldsymbol{x}_{\tau_i} - \left(\bar{\beta}_{\tau_i} - \frac{\bar{\alpha}_{\tau_i}}{\bar{\alpha}_{\tau_{i-1}}}\sqrt{\bar{\beta}_{\tau_{i-1}}^2 - \tilde{\sigma}_{\tau_i}^2}\right) \boldsymbol{\epsilon}_{\boldsymbol{\theta}}(\boldsymbol{x}_{\tau_i}, \tau_i)\right), \tilde{\sigma}_{\tau_i}^2 \boldsymbol{I}\right)\end{equation} \tag{13} \]这就是加速采样的生成过程了,从原来的\(T\)步扩散生成变成了\(\dim(\boldsymbol{\tau})\)步。要注意不能直接将式(10)的\(\alpha_t\)换成\(\alpha_{\tau_i}\),因为我们说过\(\alpha_t\)是派生记号而已,它实际上等于\(\frac{\bar{\alpha}_t}{\bar{\alpha}_{t-1}}\),因此\(\alpha_t\)要换成\(\frac{\bar{\alpha}_{\tau_i}}{\bar{\alpha}_{\tau_{i-1}}}\)才对。同理,\(\tilde{\sigma}_{\tau_i}\)也不是直接取\(\sigma_{\tau_i}\),而是在将其定义全部转化为\(\bar{\alpha},\bar{\beta}\)符号后,将\(t\)替换为\(\tau_i\)、\(t-1\)替换为\(\tau_{i-1}\),比如式(11)对应的为\(\tilde{\sigma}_{\tau_i}\)
\[\begin{equation}\sigma_t = \frac{\bar{\beta}_{t-1}\beta_t}{\bar{\beta}_t}=\frac{\bar{\beta}_{t-1}}{\bar{\beta}_t}\sqrt{1 - \frac{\bar{\alpha}_t^2}{\bar{\alpha}_{t-1}^2}}\quad\to\quad\frac{\bar{\beta}_{\tau_{i-1}}}{\bar{\beta}_{\tau_i}}\sqrt{1 - \frac{\bar{\alpha}_{\tau_i}^2}{\bar{\alpha}_{\tau_{i-1}}^2}}=\tilde{\sigma}_{\tau_i}\end{equation} \tag{14} \]可能读者又想问,我们为什么干脆不直接训练一个\(\dim(\boldsymbol{\tau})\)步的扩散模型,而是要先训练\(T>\dim(\boldsymbol{\tau})\)步然后去做子序列采样?笔者认为可能有两方面的考虑:一方面从\(\dim(\boldsymbol{\tau})\)步生成来说,训练更多步数的模型也许能增强泛化能力;另一方面,通过子序列\(\tau\)进行加速只是其中一种加速手段,训练更充分的TT步允许我们尝试更多的其他加速手段,但并不会显著增加训练成本。
Reference
[1] https://yang-song.net/blog/2021/score/#score-based-generative-modeling-with-stochastic-differential-equations-sdes # Generative Modeling by Estimating Gradients of the Data Distribution
[2] https://lilianweng.github.io/posts/2021-07-11-diffusion-models/ # What are Diffusion Models?
[3] https://blog.csdn.net/qq_41895747/category_11504878.html # Diffusion Models与深度学习
[4] https://github.com/labmlai/annotated_deep_learning_paper_implementations # 代码分析
[5] https://zhuanlan.zhihu.com/p/567780741 # Diffusion models代码解读:入门与实战
[6] https://zhuanlan.zhihu.com/p/68748778 # 【炼丹技巧】指数移动平均(EMA)的原理及PyTorch实现
[7] https://zhuanlan.zhihu.com/p/441774076 # Inception Score (IS) 与 Fréchet Inception Distance (FID)
[8] https://blog.csdn.net/qq_41895747/article/details/122764463?spm=1001.2014.3001.5501 # 为什么Diffusion Models钟爱U-net结构?
[9] 苏剑林. (Jun. 13, 2022). 《生成扩散模型漫谈(一):DDPM = 拆楼 + 建楼 》[Blog post]. Retrieved from https://kexue.fm/archives/9119
[10] 苏剑林. (Jul. 06, 2022). 《生成扩散模型漫谈(二):DDPM = 自回归式VAE 》[Blog post]. Retrieved from https://kexue.fm/archives/9152
[11]苏剑林. (Jul. 19, 2022). 《生成扩散模型漫谈(三):DDPM = 贝叶斯 + 去噪 》[Blog post]. Retrieved from https://kexue.fm/archives/9164
[12]苏剑林. (Jul. 27, 2022). 《生成扩散模型漫谈(四):DDIM = 高观点DDPM 》[Blog post]. Retrieved from https://kexue.fm/archives/9181