线段树专题
一、线段树基础
1. 线段树简介
线段树是算法竞赛中常用的用来维护区间信息的数据结构。
线段树可以在很小的时间复杂度内实现 单点修改、区间修改、区间查询(即区间求和,求区间 \(max\) ,求区间 \(min\) ,区间 \(gcd\) 等)操作。
但是,线段树所维护的信息,需要满足区间加法。
区间加法:如果一个区间 \([l,r]\)(线段树中一个点表示一个区间)满足区间加法的意思是一个区间 \([l,r]\) 的线段树维护的信息(即区间最大值,区间最小值,区间和,区间 \(gcd\) 等),可以由两个区间 \([l,mid]\) 和 \([mid+1,r]\)合并而来。
2. 线段树的基本概念
线段树,是一种基于分治思想的二叉搜索树。它支持的所有操作都可以 \(O(logn)\) 的时间复杂度完成。
但是线段树有个很大的特点:线段树的题目可以调上一整天
线段树的 基本特点:

- 线段树的每一个节点表示一个区间
- 线段树有唯一根,这个根表示的所有会被线段树统计的总区间,一般情况下,根表示的区间就是 \([1,n]\)
- 线段树的叶子节点表示的区间为 \([x,x]\) ,且长度为 \(1\)
- 线段树中如果一个节点表示的区间是 \([l,r]\) ,且这个点不为叶子节点,即 \(l≠r\),那么这个节点的左子树的根表示的区间就是 \([l,mid]\) 这个节点的右子树的根表示的区间就是 \([mid+1,r]\),其中 \(\large mid=⌊\frac{l+r}{2}⌋\)。
3.线段树的存储方式
直接采用堆存储方式,即一颗线段树的跟的编号是 \(1\) ,设一个不为根的节点编号 \(x\) ,则这个点的父节点是 \(⌊\frac{x}{2}⌋\) ,他的两个子节点的编号分别是 \(2×x\) 和 \(2×x+1\) 。为了线段树的节点不超过存储范围,一般线段树都要开 \(4×n\) 的空间,即区间总长度的 \(4\) 倍。
因为一颗线段树最多是一颗满二叉树,而满二叉树的最后一层是\(n\) 个点,前面的点数是 \(n−1\) ,所以一共要 \(2×n−1\) 的空间,但由于线段树有可能最后一层节点还有子节点,比如说 \(n=10\) 的时候,如图:
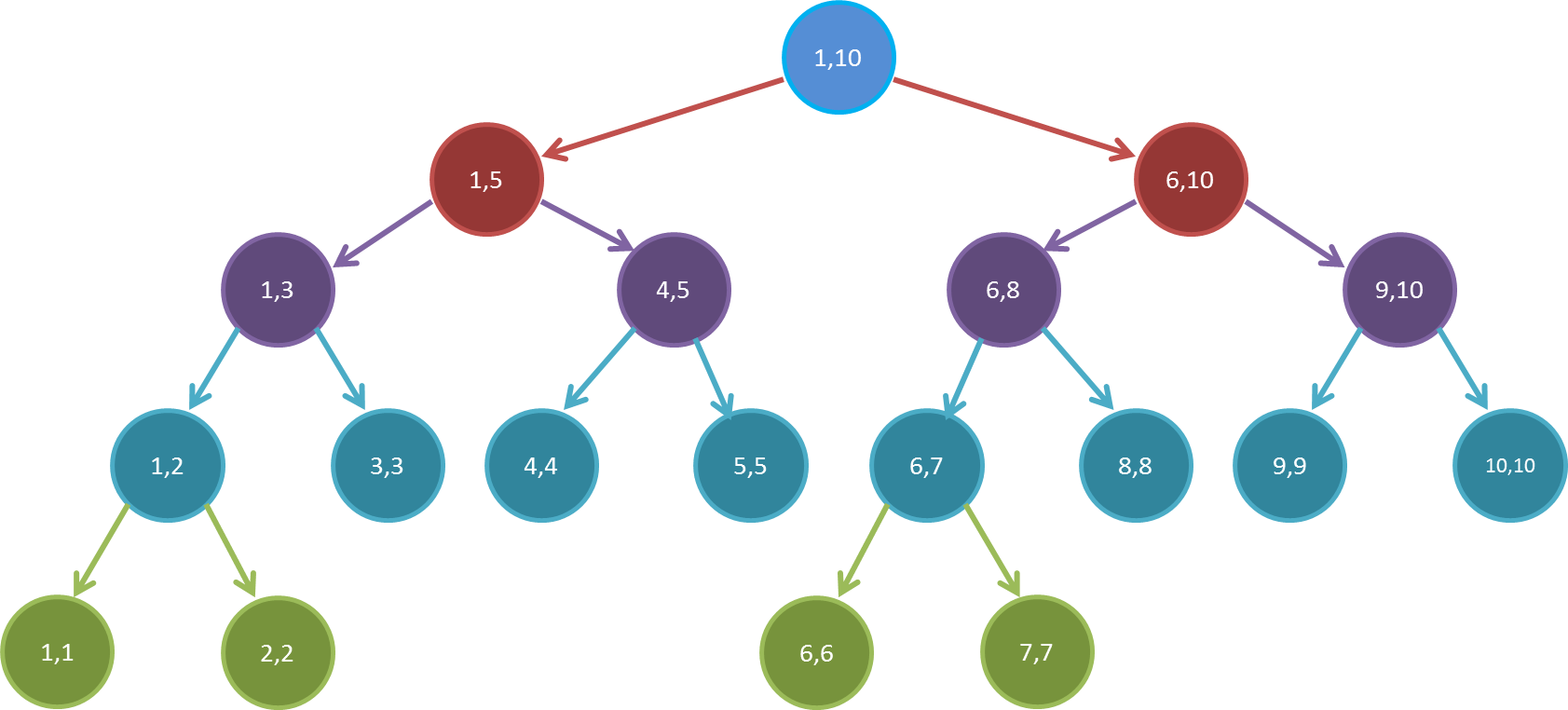
这里就是一个例子,最后一层是多出来的,而最后一层节点最多 \(2×n\) 个节点,最坏情况下就最右边两个节点,最右下角的一个节点的编号是 \(2×n−1+2×n=4×n−1\) ,所以线段树一般开 \(4×n\) 。
4.建立线段树
思路
我们递归遍历初始区间,把遍历到的所有节点表示的区间记录下来,如果这个节点不是叶子节点(即区间长度大于\(1\)),那么就分别遍历左子树和右子树,否则就是叶子节点,不仅要把表示的区间记录下来,还要把线段树维护的信息也记录下来,维护的信息在叶子节点上基本上就是这个数本身。
时间复杂度 \(O(logn)\)
代码
struct Node {
int l,r;
LL sum; //这里可以维护任何满足区间加法的信息,这里就用区间求和了
}tr[N << 2]; //要开四倍空间
void pushup (int u) { //这里只有区间和,区间和就是由一个点的左右子节点的和相加
tr[u].sum = tr[u << 1].sum + tr[u << 1 | 1].sum;
}
void build (int u,int l,int r) { //当前正在下标为u的点,这个点表示的区间是[l,r]
if (l == r) {
tr[u] = {l,r,a[l]};
return ;
}
tr[u] = {l,r}; //记得存储当前点表示的区间,否则你会调上一整天
int mid = l + r >> 1;
build (u << 1,l,mid),build (u << 1 | 1,mid + 1,r); //u << 1就是u * 2,u << 1 | 1就是u * 2 + 1
pushup (u); //pushup函数的意思是把某一个节点的信息有他的子节点算出来
}
5.单点修改
思路
我们通过二分查找的形式找到要修改的点,然后把找的过程上的链都修改一下。
时间复杂度 \(O(logn)\)
代码
void modify (int u,int x,int v) { //当前这个点是下标为u的点,要把第x个数修改成d
if (tr[u].l == tr[u].r) {
tr[u].sum = v; //如果当前区间只有一个数,那么这个数一定是要修改的。
return ;
}
int mid = tr[u].l + tr[u].r >> 1;
if (x <= mid) modify (u << 1 , x , v); //如果在左边就递归修改左半边区间
else modify (u << 1 | 1 , x , v); //如果在右边就递归修改右半边区间
pushup (u) //记得更新信息
}
6.区间修改
思路1
线段树的区间修改大体分为两步
- 找到区间中全部都是要修改的点的线段树中的区间
- 修改这一段区间的所有点
我们先解决第 \(1\) 步:
我们从根节点(根节点一定包含所有点,既包含修改区间)出发,一直往下走,直到当前区间中的元素全部都是被修改元素。
当左区间包含整个被修改区间时,我们就递归到左区间;
当右区间包含整个被修改区间时,我们就递归到右区间;
否则区间的样子就如下图所示:
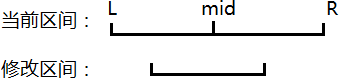
此时该怎么办呢?
不过,通过思考,我们可以发现,被修改区间中的元素间,两两之间都不会产生影响。
所以,我们可以把被修改区间分解成两段,使得其中的一段完全在左区间,另一端完全在右区间。
很明显,直接在 \(mid\) 的位置将该区间切开是最好的。如下图所示:
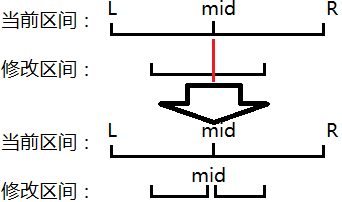
如果当前区间包含了修改区间的话就直接修改,把区间里的每一个数遍历一遍。
时间复杂度 \(O(nlogn)\)
代码
void modify (int u,int l,int r,int d) { //当前遍历到的点下标是u,要将区间[l,r]增加d
if (tr[u].l == tr[u].r) { //叶子节点
tr[u].sum += d;
return ;
}
int mid = tr[u].l + tr[u].r >> 1; //注意是tr[u].l和tr[u].r
if (l <= mid) modify(u << 1,l,r,d); //左边有修改区间,就递归左半边
if (r >= mid + 1) modify(u << 1 | 1,l,r,d); //右边有修改区间,就递归右半边
pushup (u); //要记得要把这个点的信息更新一下
}
思路2
欸,你不是说线段树所有操作都是 \(O(logn)\) 的吗?现在怎么来了一个 \(O(n)\) 的?
这不就是思路 \(2\) 啊。。。
为提高线段树的修改效率,就要引入一个好东西:懒标记
懒标记就是我们在做修改操作时能用来偷懒的标记
来自封禁的一个故事:
\(A\) 有两个儿子,一个是 \(B\),一个是 \(C\)。
有一天 \(A\) 要建一个新房子,没钱。刚好过年嘛,有人要给 \(B\) 和 \(C\) 红包,两个红包的钱数相同都是 \(1\) 元,然而因为 \(A\) 是父亲所以红包肯定是先塞给 \(A\) 咯~
理论上来讲 \(A\) 应该把两个红包分别给 \(B\) 和 \(C\),但是……缺钱嘛,\(A\) 就把红包偷偷收到自己口袋里了。
\(A\) 高兴地说:「我现在有 \(2\) 份红包了!我又多了 \(2×1=2\) 元了!哈哈哈~」
但是 \(A\) 知道,如果他不把红包给 \(B\) 和 \(C\),那 \(B\) 和 \(C\) 肯定会不爽然后导致家庭矛盾最后崩溃,所以 \(A\) 对儿子 \(B\) 和 \(C\) 说:「我欠你们每人 \(1\) 份 \(1\) 元的红包,下次有新红包给过来的时候再给你们!这里我先做下记录……嗯……我欠你们各 \(1\) 元……」
儿子 \(B\) 、\(C\) 有点恼怒:「可是如果有同学问起我们我们收到了多少红包咋办?你把我们的红包都收了,我们还怎么装?」
父亲 \(A\) 赶忙说:「有同学问起来我就会给你们的!我欠条都写好了不会不算话的!」
至于懒标记:
如果父亲 \(A\) 把钱给 \(B\) 和 \(C\) ,接着。。。 \(A\) 就没钱了。没错!懒标记就是故事中的记录父亲 \(A\) 没给的钱账本!
懒标记就是区间修改时偷懒用的,所以叫懒标记。
他主要解决了一个问题:如修改区间包含当前区间,就在这个节点上打个标记,表示这个点在以后的代码中要修改,现在先不修改。
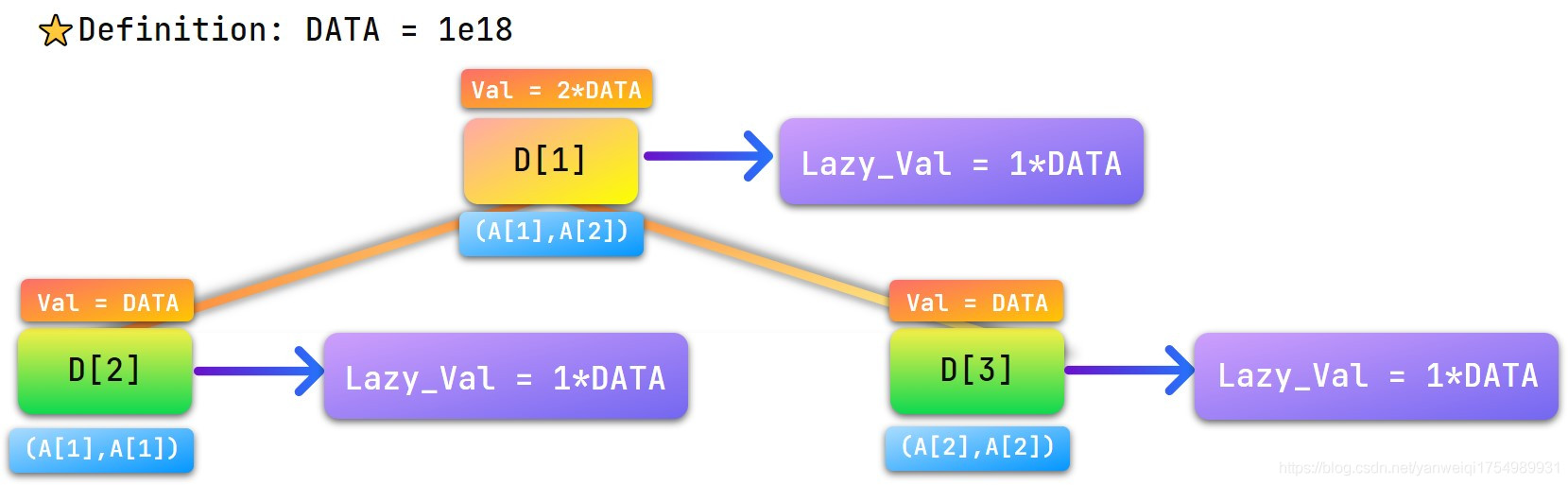
懒标记的具体意思:我觉得 \(y\) 总的懒标记意思比较好:如果一个点上打的一个懒标记,那么表示这个点的所有子节点都要变化这个懒标记(可以是加减乘除,\(max\),\(min\),\(gcd\)等等),注意!懒标记没有包含当前点!
具体见图:
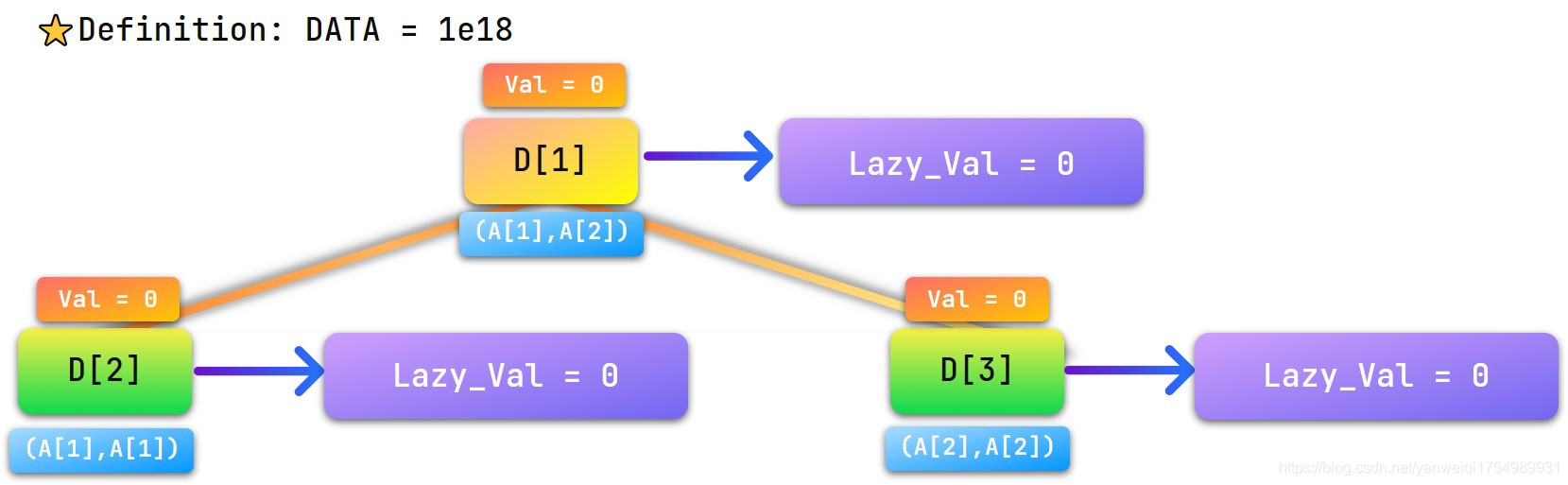
我们给区间 \([1,2]\) 加上 \(DATA=1e18\) (图左上角)
因为第一个节点包含了所有修改区间,所以我们把加的数挂在 第一个节点 上,区间修改就完成了。
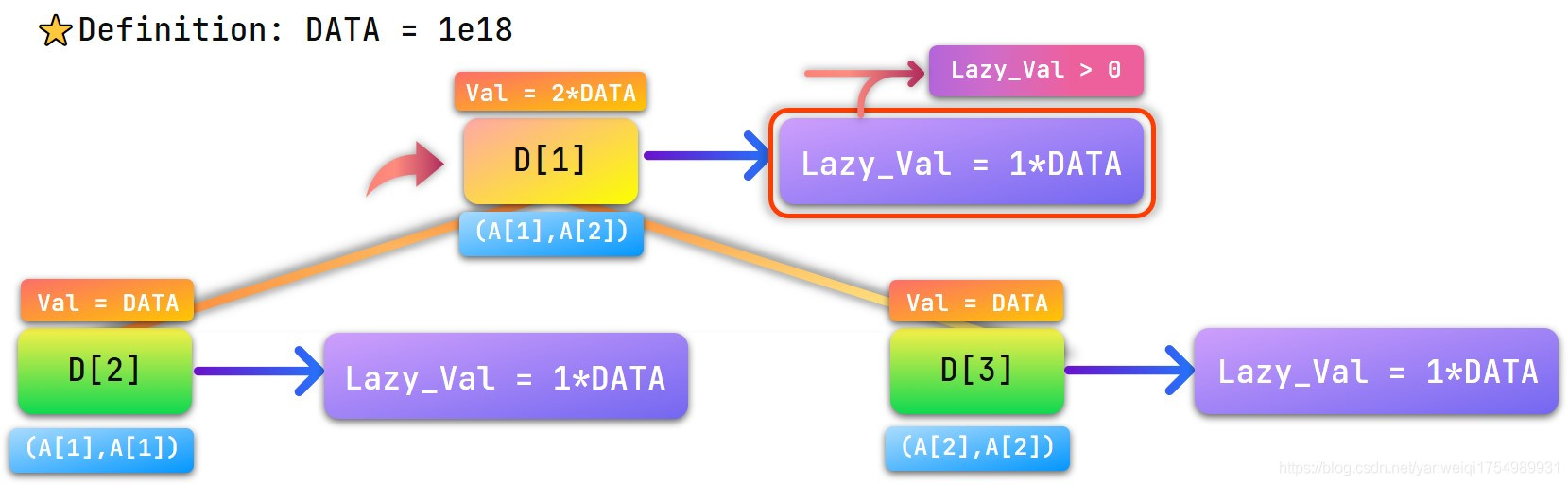
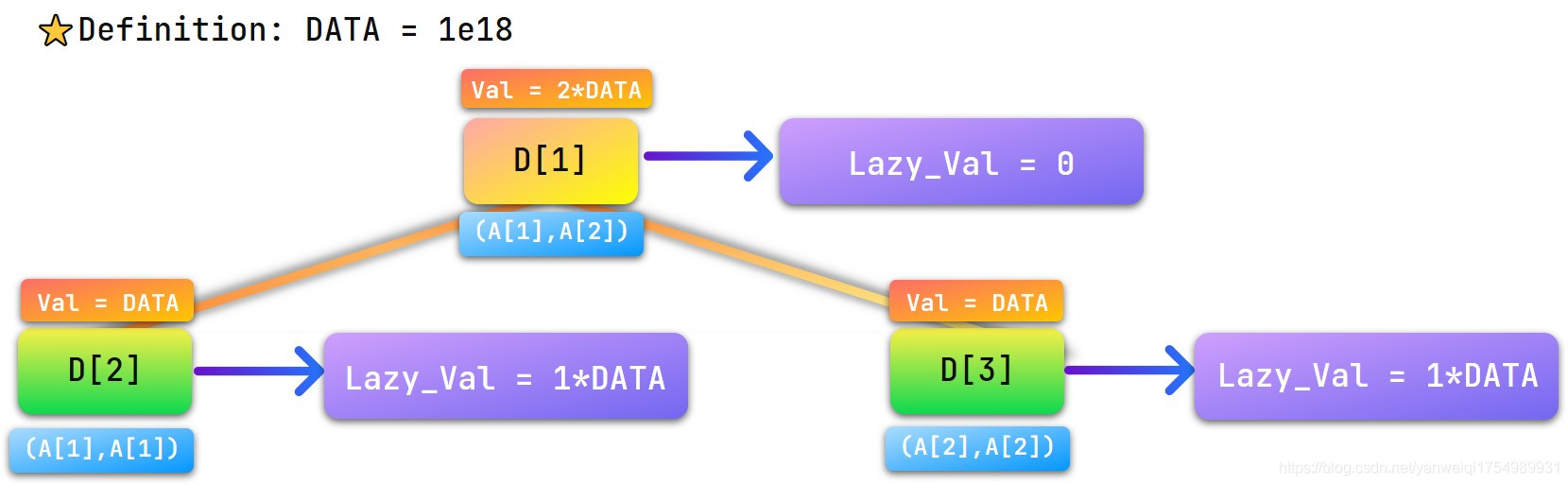
当然,还有一个细节问题,就是如果一个点有懒标记,要先把他的懒标记下传,就是把懒标记给他的两个儿子,这就是我们要实现的 \(pushdown\) 函数。下面几张图片就展示了懒标记下传的过程。
代码2
void pushdown (int u) { //下传标记函数
auto &root = tr[u],&left = tr[u << 1],&right = tr[u << 1 | 1]; //加了引用符号只要修改这个变量就会修改他被赋值的变量
if (root.tag) { //有懒标记才下传
left.tag += root.tag,left.sum += (LL)(left.r - left.l + 1) * root.tag; //这里的子节点要加上懒标记,因为这里懒标记的意思是不包括当前节点
right.tag += root.tag,right.sum += (LL)(right.r - right.l + 1) * root.tag; //同理
root.tag = 0; //懒标记记得清零
}
}
void modify (int u,int l,int r,int d) { //当前遍历到的点下标是u,要将区间[l,r]增加d
if (l <= tr[u].l && tr[u].r <= r) {
tr[u].sum += (LL)(tr[u].r - tr[u].l + 1) * d;
tr[u].tag += d; //这里我才用了y总的懒标记的意思,一个点所有的子节点都加上d,而前一行时加上根节点的数,因为不包括根节点。
return ;
}
pushdown (u); //一定要分裂,只要记牢在递归左右区间之前,就要分裂
int mid = tr[u].l + tr[u].r >> 1; //注意时tr[u].l和tr[u].r
if (l <= mid) modify (u << 1,l,r,d); //左边有修改区间,就递归左半边
if (r >= mid + 1) modify (u << 1 | 1,l,r,d); //右边有修改区间,就递归右半边
pushup (u); //要记得要把这个点的信息更新一下
}
7.区间查询
思路
区间修改类似区间修改,只不过变为查询了。
代码
LL query(int u,int l,int r) {
if (l <= tr[u].l && tr[u].r <= r) return tr[u].sum;
pushdown (u); //在递归之前一定要分裂
int mid = l + r >> 1;
LL sum = 0;
if (l <= mid) sum += query_sum (u << 1,l,r); //左半边有被查询到的数据,就递归左半边
if (r >= mid + 1) sum += query_sum (u << 1 | 1,l,r); //右半边有被查询到的数据,就递归右半边
return sum;
}
时间复杂度 \(O(logn)\)
二、题单
(1)、单点修改
\(AcWing\) \(1275\). 最大数[单点修改区间查询]
\(AcWing\) \(245\). 你能回答这些问题吗[单点修改区间查询]
\(AcWing\) \(246\). 区间最大公约数[单点修改区间查询+差分+更相减损数]
(2)、区间修改
\(HDU\) \(1698\) \(Just\) \(a\) \(Hook\)[黄海补充+区间修改统一值+区间查询]
\(HDU\) \(3577\) \(Fast\) \(Arrangement\) [黄海补充+线段树+区间修改+维护最大值]
\(POJ\) \(3264\) \(Balanced\) \(Lineup\)[黄海补充+线段树+维护最大值、最小值]
\(AcWing\) \(243\). 一个简单的整数问题[区间增加一个值+区间查询]
\(HDU\) \(3333\) \(Turing\) \(Tree\) [黄海补充+线段树(树状数组)+离线操作+数字去重求区间和]
\(POJ\) \(2828\) \(Buy\) \(Tickets\)[黄海补充+线段树+二分]
(3)、扫描线法
\(AcWing\) \(1228\). 油漆面积[扫描线+线段树,黄海补充]
(4)、线段树优化建图
(5)、线段树维护树上信息
POJ 3321 Apple Tree [\(dfs\)序求子树节点和]
据说线段树还可以应用bfs序,目前还没有找到合适的练习题,挖坑待填吧~
(6)、线段树维护区间可合并信息
\(POJ\) \(2777\) \(Count\) \(Color\)
(7)、线段树维护区间不可合并信息(暴力计算)
\(GSS4\) - \(Can\) \(you\) \(answer\) \(these\) \(queries\) \(IV\) [暴力开方]
\(P4145\) 上帝造题的七分钟 \(2\) / 花神游历各国
这个其实就是上面那道题,一模一样,输出有点差别而已。
\(CF438D\) \(The\) \(Child\) \(and\) \(Sequence\)[暴力取模]
(8)、线段树维护最大子段和
\(GSS1\) - \(Can\) \(you\) \(answer\) \(these\) \(queries\) \(I\) [区间最大子段和]
\(GSS3\) - \(Can\) \(you\) \(answer\) \(these\) \(queries\) \(III\)[区间最大子段和+单点修改]
\(GSS5\) - \(Can\) \(you\) \(answer\) \(these\) \(queries\) \(V\)[有范围限制的区间最大子段和]
(9)、线段树与思维
\(HDU\) \(5649\) \(DZY\) \(Loves\) \(Sorting\)
(10)、线段树分裂与合并
\(P4556\) [\(Vani\)有约会]雨天的尾巴 /【模板】线段树合并
(11)、可持久化线段树(主席树)
codevs 1080 (单点修改+区间查询)
codevs 1081 (区间修改+单点查询)
codevs 1082 (区间修改+区间查询)
codevs 3981 (区间最大子段和)
Bzoj 3813 (区间内某个值是否出现过)
Luogu P2894 (区间连续一段空的长度)
codevs 2000 (区间最长上升子序列)
codevs 3044 (矩阵面积求并)
Hdu 1698 (区间染色+单次统计)
Poj 2777 (区间染色+批量统计)
Hdu 4419 (多色矩形面积并)
Poj 2761 (区间第K大)
Hdu 2305 (最值维护)