写在开头的话
在回到学校之后的几天后,我结束了cmu15418并行系统的学习,怎么说呢?这门课确实让我学到了不少,比如各种并行性的优化,但是我觉得自己还是有些吃力。包括在实习的最初,因为使用的语言是cpp,有不少使用cmake的经历,虽然我学习了cmake的语法,但是对于cmake工作的本质确实模模糊糊。程序如何进行编译,gcc各种编译参数到底是什么意思?动态库链接又是如何执行的。这一切搞得我写c++时候就像是有一层雾一样,我始终搞不清我的代码到底是如何work的。正因为如此,所以我决定不继续学习高级的计算机课程。我必须把编译、链接这一套给弄得明明白白了。
月初的时候,我浏览了一下各种图书和课程,发现CSAPP这本书正是我在找的一本书。整本书都在讲程序是如何从源代码到系统中的进程,这一过程。于是果断下单

不得不说,真是有点小贵,这可能是我买过的最贵的书了。o(╥﹏╥)o
搭配,b站的cmu课程同步进行学习。
我写下这段话的时候,刚好过去了一个星期也就是7号。目前一切进度还算OK,我原本以为纯英文的书会读得很吃力,但好像并没有,技术书籍基本上都是常见单词,语法可以说几乎没有。感觉英文并没有成为我的阻扰,开心,说明我现在阅读英语技术书籍基本上没问题了。(*▽*)
Representing and Manipulating Informatica
这个系列的笔记说实话,我不是很明白我应该记录什么?因为很多内容需要和书本结合,而我如何把书本一块写上来,没必要而且我也不想浪费时间。所以我的打算是将这个笔记作为自己学习阶段的review。把自己觉得很重要的知识点记录下来。因为只是自己review,所以不拘泥于书本的顺序。
大小端
小端这个这个概念其实从我接触计算机的时候就一直困惑着我,包括后来考研也没有把这块给弄清楚。
-
内存地址从高地址往低地址进行生长。数据无论是c++中class还是array都是一串比特流,是从低地址一直放到高地址。
-
任何object的地址,比如c++中的class或者数组都可以被视为一个object。而最低的地址用于表示object的起始地址。
-
数组有些特殊:
例如
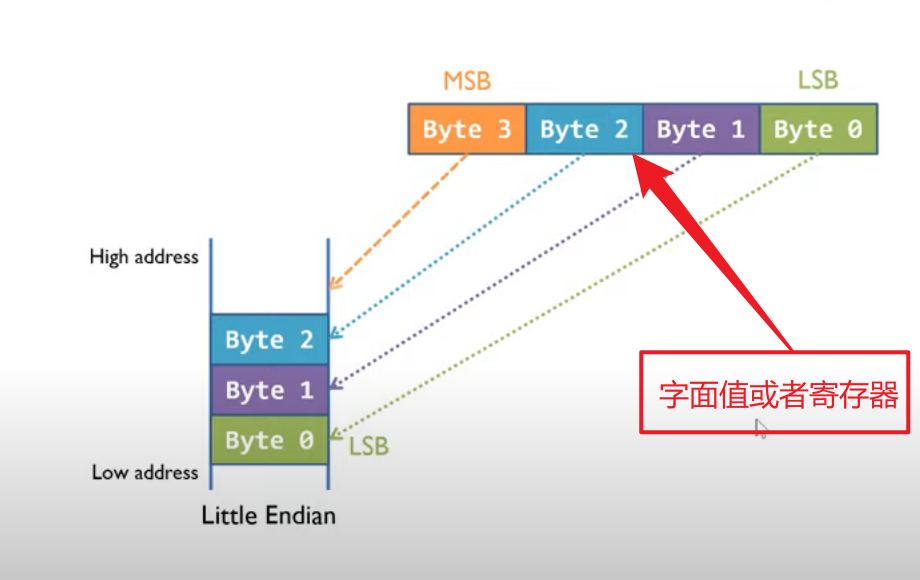
short a[] = {1, 2, 3},那么从低位到高位进行存放bit,0x010002000300。数组是按index从低地址放到高地址,数组中元素是按照byte从低地址放到高地址,这看起来有点奇怪。但是记住这张图就行了
我自己也做了一些试验:
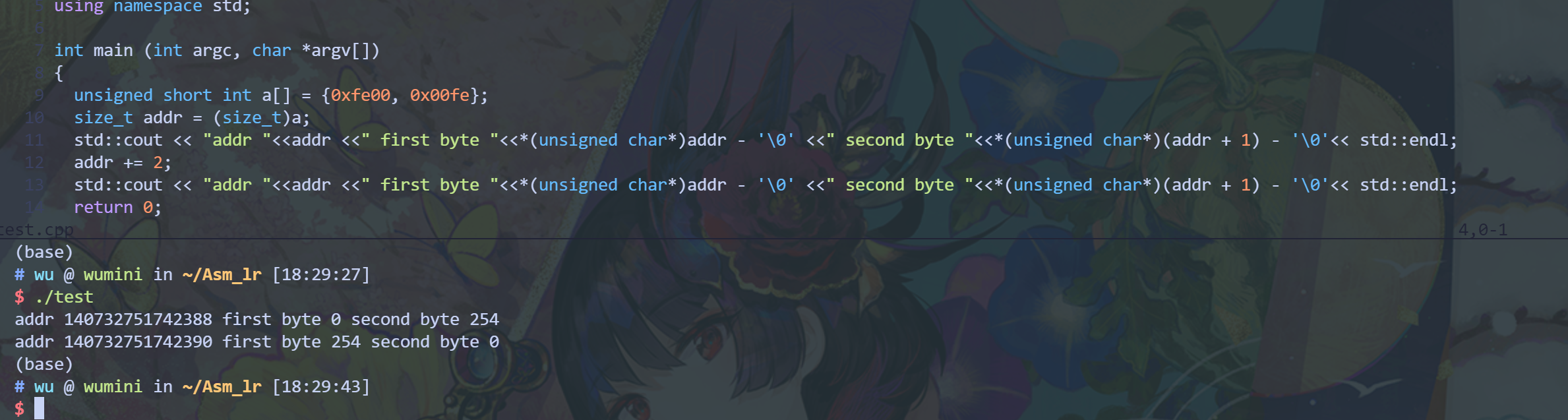
可以看到bit是翻转的。
-
普通寄存器中的endian。按道理寄存器中是没有endian的概念了,但因为x86-64同时保留了
rax与eax这些概念。导致我们访问一个64位的寄存器,实际上是一个big endian的顺序。比如数字0x00000001,存放在eax中,那么有效位1实际上在ax中也能看到。寄存器的字节序就是数字的表示顺序。 -
simd寄存器。在上面提到寄存器中实际上是大端,但是simd寄存器,例如
xmmm0,它可以存放4个float数值。如果我们使用_mm_set_ps(1.0, 2.0, 3.0, 4.0),其寄存器中的组织和内存的字节序如下图: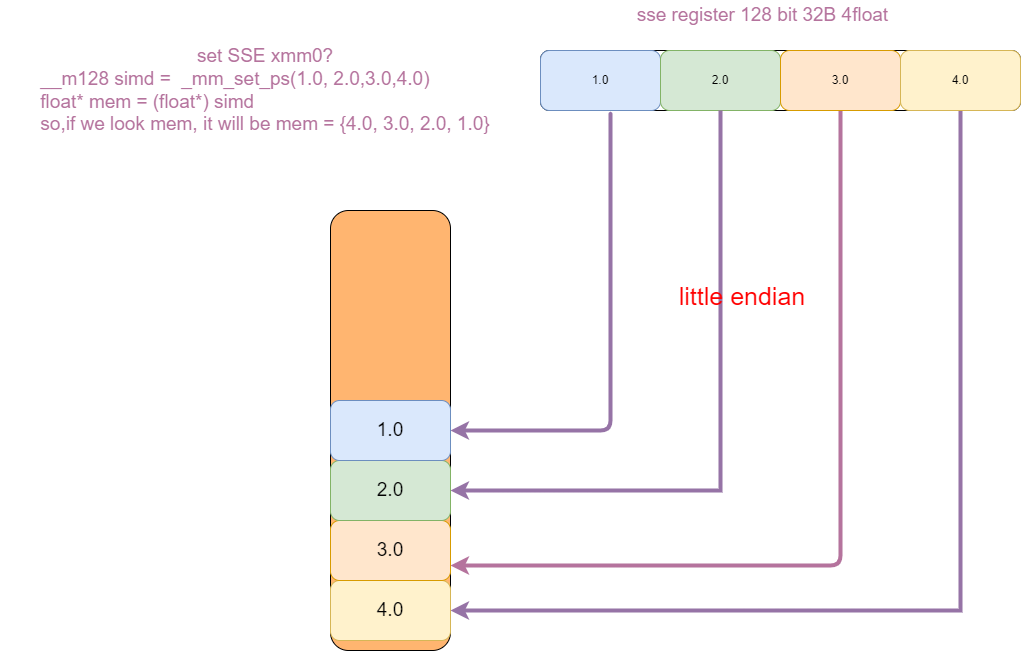
如果我们通过代码来看的话,我们可以看到,结果和我们的预期一样:
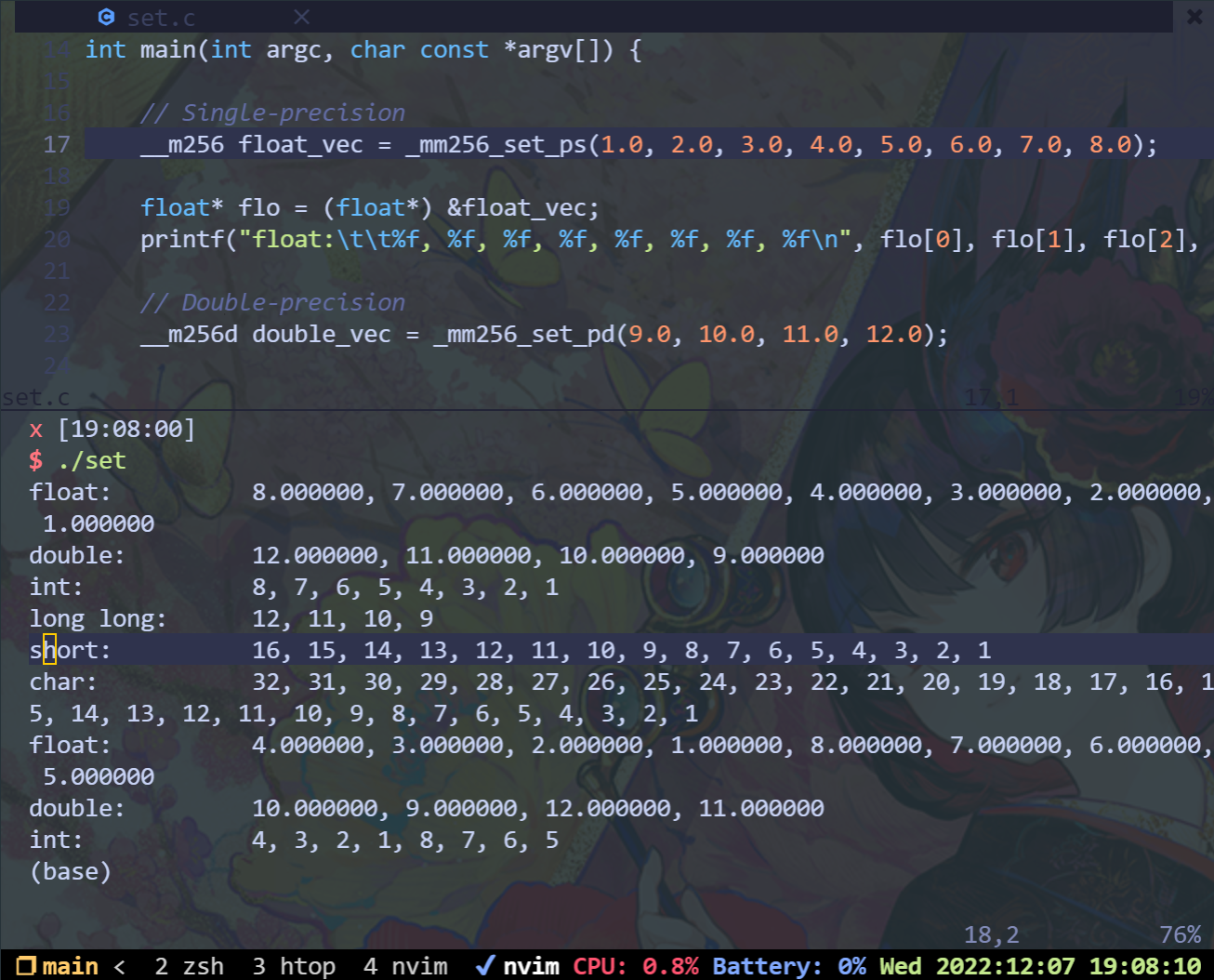
- simd中bit的index如何定义?例如hadd这个simd函数

simd寄存器中哪一端是128哪一端是0?实际通过代码实验我们确定了simd的index顺序,我们以load_ss这个函数为例子验证了我们的猜测


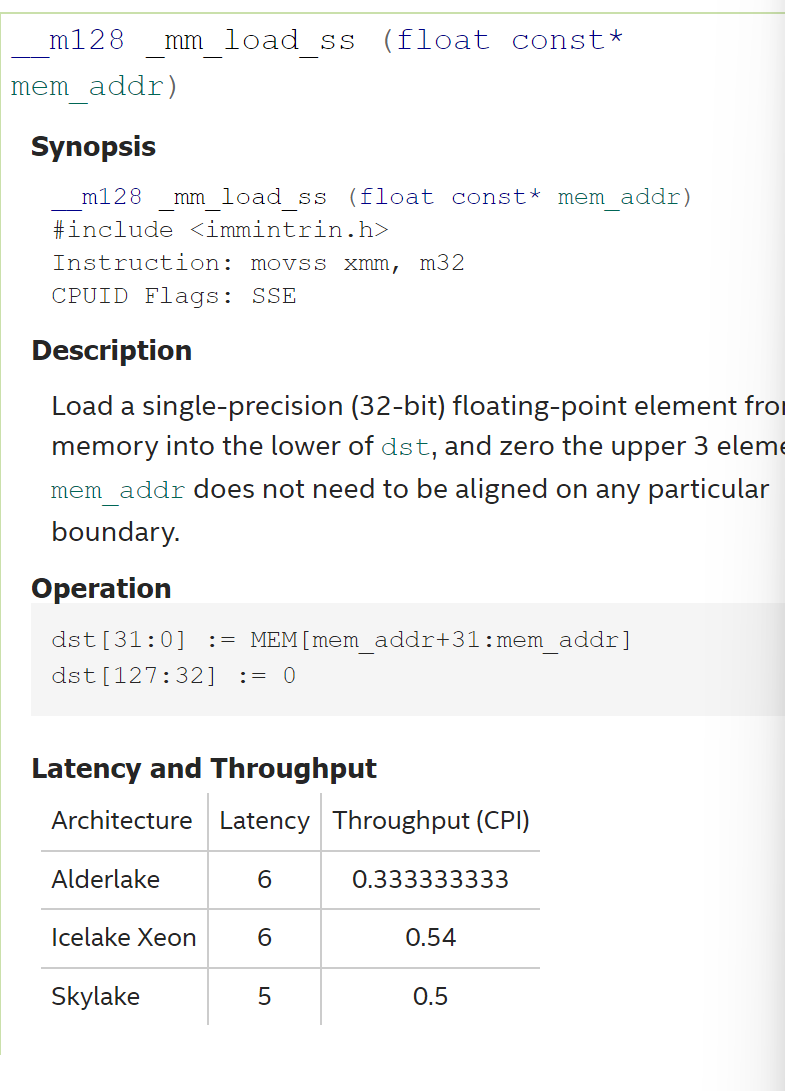
至此,我们彻底搞明白了寄存器的右端是index 0。大小端这个困惑了我多年的问题至此圆满解决,✿✿ヽ(°▽°)ノ✿
two‘s complement
补数的定义其实很简单,就是 \(B 2 T(X)=-x_{w-1} \cdot 2^{w-1}+\sum_{i=0}^{w-2} x_i \cdot 2^i\) ,正数转负数,相当于bit翻转然后加一。
|TMIN| = TMAX + 1 补数负数能比正数多表示一个数值。c中有limits.h
c++或者c语言unsigned和signed进行比较,会将signed转换为unsigned值,相当于reinterpret_cast。例如-1作为short int,其二进制表示为0xffff,这也是unsigned short的最大表示范围。UMAX = 2 *TMAX + 1
unsigned 与signed之间转换:
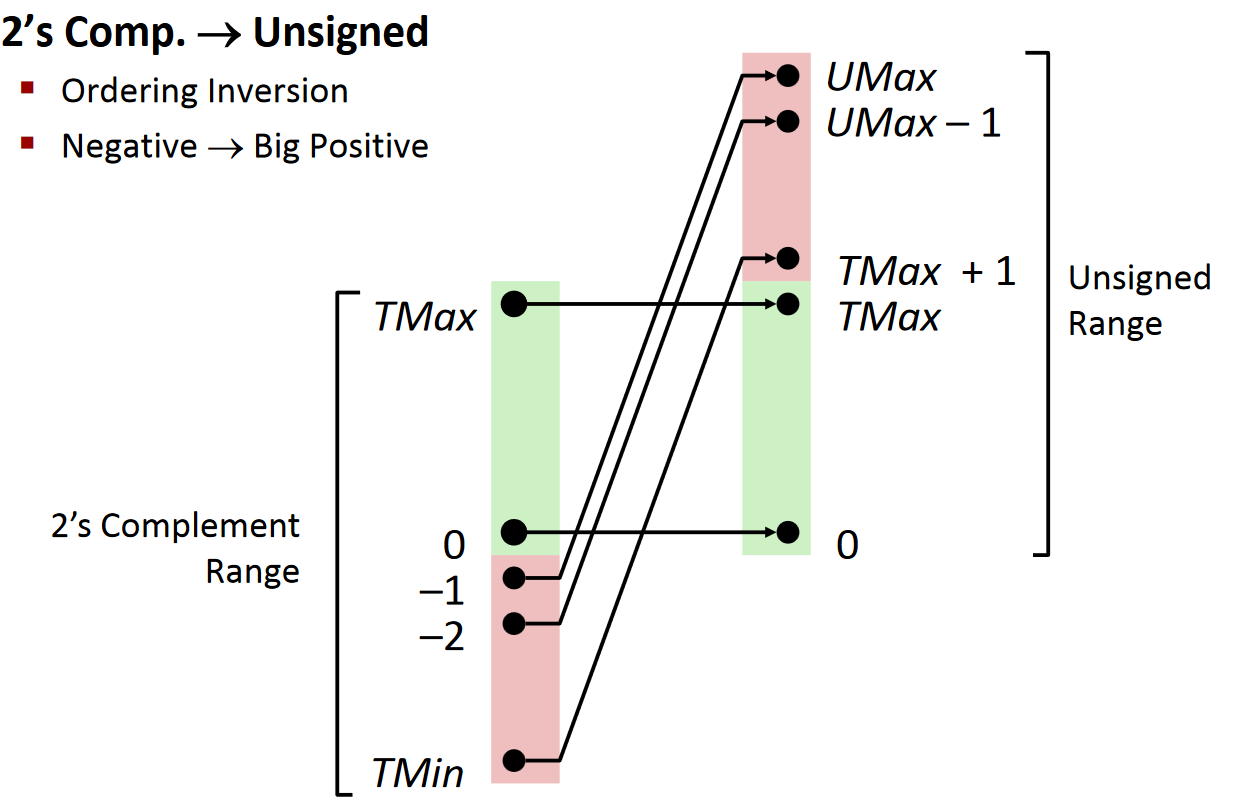
整数溢出
unsigned addition overflow detecting:
s = x+y,如果s < x那么说明发生了溢出
signed的溢出也很简单,如果两个正数相加会发生负溢出,如果两个负数相加会发生正溢出。
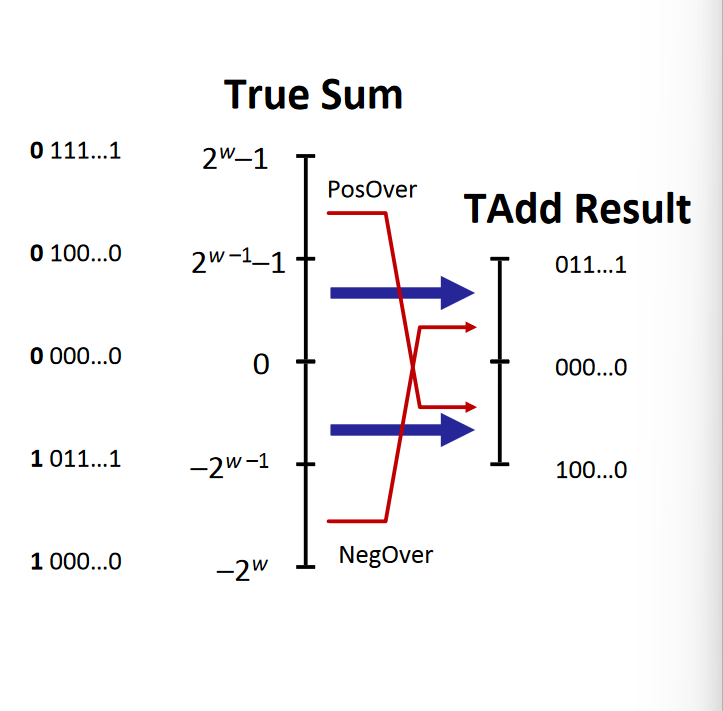
float

注意这里的

review slides才看到原来NaN是一个表示形式

float类型的round,小于half向下取整,大于half 向上round,等于half,round到最近的偶数
