目前做了两道题
现在对分层图的理解是建立好几个图,然后每层图,每个点之间建边
通信线路
在郊区有 NN 座通信基站,PP 条 双向 电缆,第 ii 条电缆连接基站 AiAi 和 BiBi。
特别地,11 号基站是通信公司的总站,NN 号基站位于一座农场中。
现在,农场主希望对通信线路进行升级,其中升级第 ii 条电缆需要花费 LiLi。
电话公司正在举行优惠活动。
农产主可以指定一条从 11 号基站到 NN 号基站的路径,并指定路径上不超过 KK 条电缆,由电话公司免费提供升级服务。
农场主只需要支付在该路径上剩余的电缆中,升级价格最贵的那条电缆的花费即可。
求至少用多少钱可以完成升级。
输入格式
第 1 行:三个整数 N,P,K。
第 2..P+1 行:第 i+1 行包含三个整数 Ai,Bi,Li。
输出格式
包含一个整数表示最少花费。
若 11 号基站与 N 号基站之间不存在路径,则输出 −1−1。
数据范围
0≤K<N≤1000,
1≤P≤10000,
1≤Li≤1000000
输入样例:
5 7 1
1 2 5
3 1 4
2 4 8
3 2 3
5 2 9
3 4 7
4 5 6输出样例:
4
前k个线路可以免费,也就是说,需要建立一个k层的图
这个的分层似乎和其他的不太一样,目前还是有些疑惑,理解后再补
具体看代码和注释吧,来自蓝书
通信线路
#include<iostream>
#include<cstring>
#include<queue>
#define int long long
#define mkp make_pair
#define sec second
#define fir first
using namespace std;
const int maxn=2e5+10;
//题目是分层图
//我们把免费操作转化成零边,如果进行免费操作,就进入下一层
//就是说,可以建好几层图,第0层就是一条边也不去掉,第1曾去掉最大的那条边,第2曾去掉前2大的边.....
int n,p,k;
int head[maxn],nex[maxn],ver[maxn],edge[maxn],tot;
int d[1001][1001];//或者是d[i][j]是到i点,去掉j条边后的最大值中的最小值(看到这里应该想到似乎可以二分)
bool ju[1001][1001];
priority_queue<pair<int, pair<int,int>>>q;
inline void add(int x,int y,int z)
{
ver[++tot]=y;
edge[tot]=z;
nex[tot]=head[x];
head[x]=tot;
}
void dijkstra()
{
memset(d,0x7f7f,sizeof(d));
d[1][0]=0;
q.push(make_pair(0,mkp(1,0)));
while(q.size())
{
int x=q.top().sec.fir,l=q.top().sec.sec;
q.pop();
if(ju[x][l])continue;//从1到x
ju[x][l]=1;
for(int i=head[x];i;i=nex[i])
{
int y=ver[i],z=edge[i];//x可以直接连到y
if(d[y][l]>max(d[x][l],z))//同一层 从x->y还有个边x,如果到y时去掉l条边后的值不如先去掉l条边到x再到y小
//(就是说走x这条路可以获得更小的值),
//为什么max(d[x],z)呢,因为此路线中的最大的中的第l+1个是d[x]或者d[x]<z的话
//就要把z插在d[x]值前面,就是说此路线中的最大的中的第l+1个变成了z
{
d[y][l]=max(d[x][l],z);
q.push(mkp(-d[y][l],mkp(y,l)));
}
if(l<k&&d[y][l+1]>d[x][l])//这里是说把x,y之间的边free掉,那么进入下一层图,至于为什么是大于,还是因为x线路存在更优解
{
d[y][l+1]=d[x][l];
q.push(mkp(-d[y][l+1],mkp(y,l+1)));
}
}
}
}
signed main()
{
cin>>n>>p>>k;
for(int i=1;i<=p;i++)
{
int x,y,z;
cin>>x>>y>>z;
add(x,y,z);
add(y,x,z);
}
dijkstra();
int ans=0x7f7f7f7f;
for(int i=0;i<=k;i++)//防止没有走k层就到n了
ans=min(ans,d[n][i]);
if(ans==0x7f7f7f7f)cout<<-1;
else cout<<ans<<endl;
return 0;
}回家的路
题目描述
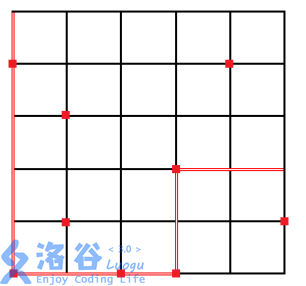
2046 年 OI 城的城市轨道交通建设终于全部竣工,由于前期规划周密,建成后的轨道交通网络由2n2n条地铁线路构成,组成了一个nn纵nn横的交通网。如下图所示,这2n2n条线路每条线路都包含nn个车站,而每个车站都在一组纵横线路的交汇处。
出于建设成本的考虑,并非每个车站都能够进行站内换乘,能够进行站内换乘的地铁站共有mm个,在下图中,标上方块标记的车站为换乘车站。已知地铁运行 1 站需要 2 分钟,而站内换乘需要步行 1 分钟。Serenade 想要知道,在不中途出站的前提下,他从学校回家最快需要多少时间(等车时间忽略不计)。
输入格式
第一行有两个整数n,mn,m。
接下去mm行每行两个整数x,yx,y,表示第xx条横向线路与第yy条纵向线路的交
汇站是站内换乘站。
接下去一行是四个整数x_1,y_1,x_2,y_2x1,y1,x2,y2。表示 Serenade 从学校回家时,在第 x_1x1条横向线路与第y_1y1条纵向线路的交汇站上车,在第x_2x2条横向线路与第y_2y2条纵向线路的交汇站下车。
输出格式
输出文件只有一行,即 Serenade 在合理选择线路的情况下,回家所需要的时间。如果 Serenade 无法在不出站换乘的情况下回家,请输出-1。
输入输出样例
输入 #12 1
1 2
1 1 2 256 9
2 1
2 5
3 2
4 4
5 2
5 6
6 1
6 3
6 4
1 1 4 6276 10
2 1
2 5
3 2
4 4
5 2
5 6
6 1
6 3
6 4
6 6
1 1 4 626说明/提示
对于 30%的数据,n≤50,m≤1000;
对于 60%的数据,n≤500,m≤2000;
对于 100%的数据,n≤20000,m≤100000;
这个应该算一个典型的分层图吧,有m+2个点,那么我们按照横向和纵向建立两个图,那么总共2*m+4个点,i和i+m+2的边权为1,起点+m+2,终点+m+2的边权为0
分别按照横向和纵向排一次序,建图吧,记得是双向边
回家的路
#include<iostream>
#include<queue>
#include<vector>
#include<cstring>
#include<algorithm>
#define int long long
#define pii pair<int,int>
#define mkp make_pair
#define fir first
#define sec second
using namespace std;
const int maxn=6e6+10;
int n,m,stx,sty,enx,eny;
int ver[maxn],val[maxn],head[maxn],nex[maxn],tot,d[maxn];
struct station
{
int id;
int x,y;
}a[maxn];
bool cmp1(station i,station j)
{
if(i.x==j.x)return i.y<j.y;
return i.x<j.x;
}
bool cmp2(station _,station __)
{
if(_.y==__.y)return _.x<__.x;
return _.y<__.y;
}
priority_queue<pii>q;
bool ju[maxn];
void dijkstra(int s)
{
memset(d,0x7f7f7f,sizeof(d));
d[s]=0;
q.push(mkp(0,s));
while(!q.empty())
{
int x=q.top().sec;
q.pop();
if(ju[x])continue;
ju[x]=1;
for(int i=head[x];i;i=nex[i])
{
int y=ver[i],z=val[i];
if(d[y]>d[x]+z)
{
d[y]=d[x]+z;
q.push(mkp(-d[y],y));
}
}
}
}
inline void add(int x,int y,int z)
{
ver[++tot]=y;
val[tot]=z;
nex[tot]=head[x];
head[x]=tot;
}
inline void addd(int x,int y,int z)
{
add(x,y,z);
add(y,x,z);
}
signed main()
{
cin>>n>>m;
if(m==0)//特判一下
{
cout<<-1;
return 0;
}
for(int i=1;i<=m+2;i++)
{
cin>>a[i].x>>a[i].y;
a[i].id=i;
}
sort(a+1,a+m+3,cmp1);
for(int i=1;i<=m+1;i++)
{
if(a[i].x==a[i+1].x)
{
addd(a[i].id,a[i+1].id,(a[i+1].y-a[i].y)*2);
}
}
sort(a+1,a+m+3,cmp2);
for(int i=1;i<=m+1;i++)
{
if(a[i].y==a[i+1].y)
{
addd(a[i].id+m+2,a[i+1].id+m+2,(a[i+1].x-a[i].x)*2);
}
}
for(int i=1;i<=m;i++)addd(i,i+m+2,1);//两层图建边
addd(m+1,m+1+m+2,0);
addd(m+2,m+2+m+2,0);
dijkstra(m+1);
if(d[m+2]==0x7f7f7f)cout<<-1;
else cout<<d[m+2];
return 0;
}看这位大佬的bolg还有几个题目,有空再做吧
标签:int,短路,tot,线路,分层,maxn,include,define From: https://www.cnblogs.com/qbning/p/16632279.html